文氏图2025年3月17日 | 阅读 7 分钟 在数学中,文氏图是一种表示两个或多个集合之间关系的图。它是由约翰·文恩提出的。他以图画的形式表示不同事物群体之间的关系,这种图被称为文氏图。 在本节中,我们将学习什么是文氏图,它的类型、目的、用途,以及如何用恰当的例子来表示它。在学习文氏图之前,让我们快速回顾一下集合。 集合是事物的集合或群体。它可能包含数字、元音、动物、素数等。集合用大写字母表示,集合的元素用小写字母表示。集合的所有元素都包含在一对花括号 {} 中。 例如,E 是一个表示小于 10 的偶数的集合。我们可以用集合的形式表示它,如下所示: E={2,4,6,8} 其中 E 是集合的名称,2, 4, 6, 8 是集合的元素。我们也可以用图画的形式表示一个集合,这被称为文氏图。 什么是文氏图?表示有限集合(一组事物)之间数学逻辑或关系的图或图形称为文氏图。它用于说明集合关系。我们通常使用圆圈或椭圆来表示文氏图。它可能有一个以上的圆圈;每个圆圈代表一个集合。 假设有两个集合 A 和 B,分别包含元素 {1, 2, 3} 和 {8, 5, 9}。我们可以将这两个集合表示在文氏图中,如下图所示。 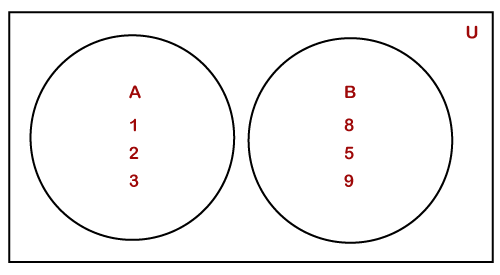 文氏图的优点
文氏图的用途文氏图用于数学,以理解集合论。我们也用它来理解对象集合之间或集合内的关系。它描绘了集合的交集和并集。 如何绘制文氏图
假设有两个集合 A 和 B,它们有一些共同的元素。这些集合的文氏图可以按如下方式绘制:  文氏图的类型文氏图有以下类型:
双集图:当两个集合相互重叠时,称为双集图。在下面的图中,有两个集合A和B,分别包含元素{a, e, i, o, u}和{a, b, c, d, e, f, g}。这两个集合中有两个共同元素,即{a, e}。让我们在文氏图中表示这种关系。  双集欧拉图:当两个集合不重叠时,称为双集欧拉图。在下面的图中,有两个集合A和B,分别包含元素{芒果、苹果、香蕉、番石榴、葡萄}和{土豆、辣椒、姜、西红柿、胡萝卜、萝卜}。集合 A 代表水果集合,集合 B 代表蔬菜集合。蔬菜和水果不匹配,所以集合中没有共同元素。让我们在文氏图中表示这两个集合。  如果一个集合完全包含另一个集合,那么它既是欧拉图也是文氏图。假设集合 A 代表动物集合,集合 B 代表食肉动物集合。很明显,不是所有的动物都是食肉动物,但反之亦然。因此,所有的食肉动物也存在于动物集合 A 中。我们可以如下在文氏图中表示:  三集图:当三个集合相互重叠时,称为三集图。在下面的图中,有三个集合A、B和C,分别包含元素{Andrew, Peter, Sam, Tom, David}、{Michael, Sam, Tom, Robert, Jack, Smith}和{David, Maria, Tom, Angelina, Michael}。集合 A、B 和 C 分别代表学习物理、化学和数学的学生姓名。在上述集合中,有些学生只学一门学科,有些学生学两门学科,有些学生学三门学科。
因此,我们可以如下在文氏图中表示:  三集欧拉图:在三集图中,当一个集合不与其他两个集合重叠时,称为三集欧拉图。假设集合 A 代表元音集合{a, e, i, o, u},集合 B 代表字母集合{a, b, c, d, e, f, g},集合 C 代表希腊字母集合{ρ,ω,φ,θ,ϵ}。我们可以如下在文氏图中表示:  三集欧拉图可以包含嵌套集合。在下面的图中,粉色事物集合可能包含浅粉色事物集合。  上面的图不是文氏图,因为两个集合(黑色事物和浅粉色事物)不重叠。 四集图:我们使用椭圆形来表示四集图,因为圆圈不再能相互重叠。椭圆形确保所有集合都相互重叠。这是表示四集图的唯一选择。  我们也使用带有曲线的三集图来表示四集图。当使用圆圈的四集图也是欧拉图时,圆圈将无法显示每对集合之间的并集。  在开始示例之前,让我们快速回顾一下集合论中使用的符号。
让我们来解决一些基于文氏图的例子。 示例 1:在一个办公室,随机选择 200 名员工进行调查。在 200 名员工中,140 人喜欢茶,120 人喜欢绿茶,80 人既喜欢茶也喜欢绿茶。根据问题-答案中提供的数据,回答以下问题。
解决方案:我们可以用文氏图表示给定的信息,其中T代表茶,G代表绿茶。 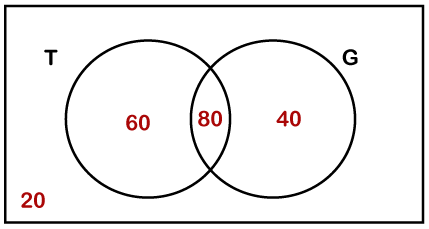
示例 2:在一项对一所学校 500 名学生进行的调查中,团队观察到
根据以上数据,回答以下问题。
解决方案 n(F) = 喜欢踢足球的学生 = 49% 由于 5% 的人喜欢玩上述任何游戏,所以 n (F ∪ H ∪ B) = 95%。 现在应用基本公式, 95% = 49% + 53% + 62% -27% - 29% - 28% + n (F ∩ H ∩ B) 求解,我们得到 n (F ∩ H ∩ B) = 15%。 现在,我们将根据我们计算出的信息绘制文氏图。请记住,图中的所有值都以百分比表示。 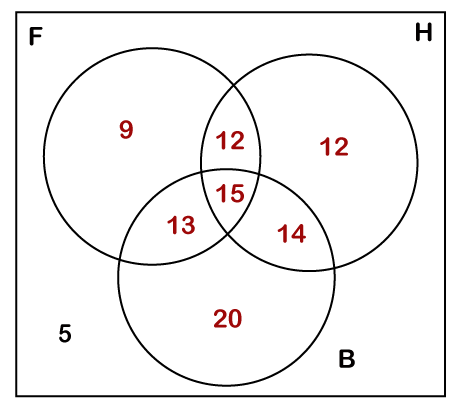 下一主题复利 |
我们请求您订阅我们的新闻通讯以获取最新更新。