单位圆2025年3月17日 | 阅读 3 分钟 在几何学中,单位圆是一种特殊的圆。它用于解释三角学概念。我们可以用它来解释从 0 度到 360 度的所有可能的角度测量。简而言之,单位圆表示所有存在的正负角度。 在本节中,我们将学习什么是单位圆、单位圆的组成部分以及如何找到单位圆上的点。 什么是单位圆?半径为单位长度的圆称为单位圆。这意味着半径为 1 个单位的圆称为单位圆。单位圆的圆心坐标为 (0, 0)。 换句话说,从圆心到圆周上任意一点的直线长度始终等于 1。 单位圆上的点单位圆上的点使数学对我们来说变得简单。例如,在单位圆中,对于任何角度 θ,正弦和余弦的三角函数值清楚地只是 sin (θ)=y 和 cos (θ)=x。 要理解单位圆上的点,我们首先学习三角学中的象限系统。下图显示了四个象限。 
下图说明了哪个象限的正弦和余弦值将为正或负。  现在转向单位圆。 首先,我们垂直和水平绘制两条割线。它将圆分为四个象限(逆时针),分别标记为第一、第二、第三、第四象限。写出每个交点的坐标。  我们可以在单位圆上定义三角函数正弦和余弦。假设 (x, y) 是单位圆上的一个点,并且从圆心到点 (x, y) 的弦与 x 轴形成 θ 角,如下图所示。那么,方程 x2+y2=1 给出以下关系 分别用余弦和正弦代入 x 和 y 的值,我们得到 cos2 θ + sin2 θ = 1  我们可以从单位圆中观察到,正弦和余弦的值永远不会大于 1 或小于 -1。因此,正弦和余弦的值介于 1 和 -1 之间。 当我们到达圆的四分之一和四分之三时(即 90°、180°、270°),我们不定义这些角度的正切。现在,我们进一步将每个象限分为四个子部分。这些部分形成 0°、30°、45°、60° 和 90° 的角度。 注意:我们不会在任何象限中考虑 0°、90°、180° 和 270°。这仅用于理解目的。要写出所有象限其他角度的值,我们必须记住三角函数值。当我们完成上述所有步骤后,第一象限如下图所示   以下单位圆显示了某些点的坐标。 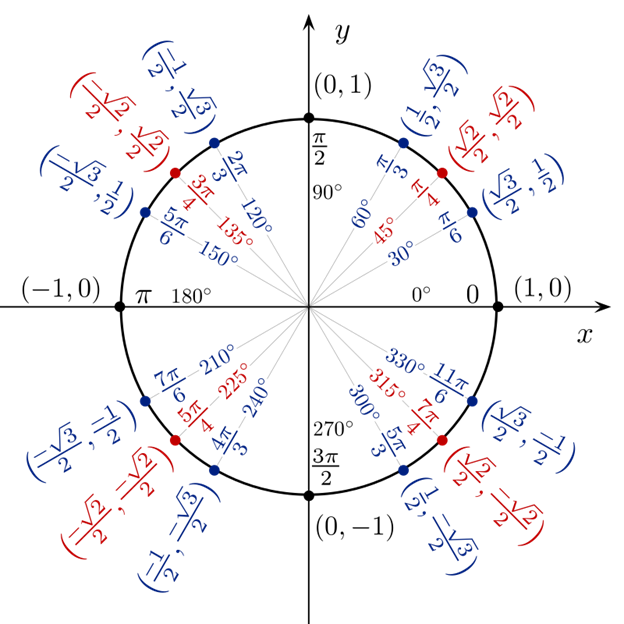 下一主题# |
我们请求您订阅我们的新闻通讯以获取最新更新。