圆柱体体积

在本节中，我们将学习圆柱体积的计算公式以及如何计算圆柱的体积，并附有适当的示例。

圆柱体是一种具有两个圆形底面的三维几何形状。它有两个圆形底面，一个在顶部，一个在底部。我们也可以将圆柱体定义为堆叠的圆形盘片的排列。圆柱体有两种类型

• 圆柱体或实心圆柱体
• 空心圆柱体

定义

能够完全填充圆柱体的立方单位数称为圆柱体的体积。换句话说，圆柱体所占的空间称为圆柱体的体积。

圆柱体积公式

它是圆柱体底面积与高之积。

空心圆柱体的体积

内部中空的圆柱体称为空心圆柱体。空心圆柱体有两个半径。一个用于内圆柱体，另一个用于由底面形成的 outer cylinder。

假设r₁是外圆的半径，r₂是内圆的半径，h是圆柱体的高度，那么空心圆柱体的体积将是

如何计算圆柱体的体积

我们可以通过将圆的面积乘以圆柱体的高度来计算圆柱体的体积。

我们知道圆的面积公式

圆的面积 (A)= πr²

将圆的面积乘以圆柱体的高度，我们就得到了圆柱体的体积。因为，

其中

π：这是一个常数，其值是3.142或22/7。

r：这是圆柱体的半径。

h：这是圆柱体的高度。

注意：半径和高度必须使用相同的单位。如果单位不同，请进行转换。

体积单位

体积的单位是立方单位或单位³。例如，如果半径和高度以厘米为单位给出，则体积也以厘米为单位，单位将是立方厘米或cm³。

让我们看一些例子。

示例 1：圆柱体的半径为 5 厘米，高度为 12 厘米。计算圆柱体的体积。取 π=。

解决方案

已知，半径 (r) = 5 cm

高度 (h) = 12 cm

π=

体积 (V) =?

我们知道圆柱体体积的公式

V= πr² h

将值代入上述公式，我们得到

因此，圆柱体的体积为 942.85 cm³。

示例 2：计算半径为 3 厘米，高度为 6 厘米的圆柱体的体积。（π=3.14）

解决方案

已知，半径 (r) = 3 cm

高度 (h) = 6 cm

π = 3.14

体积 (V) =?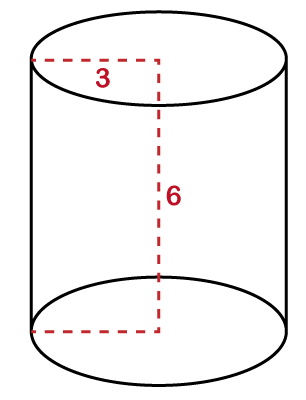

我们知道圆柱体体积的公式

V= πr² h

将值代入上述公式，我们得到

V=3.14×(3²)×6
V=3.14×9×6
V=3.14×54
V=169.56

因此，圆柱体的体积为 169.56 cm3。

示例 3：计算下图所示圆柱体的体积。

解决方案

已知，半径 (r) = 4.5 cm

高度 (h) = 8 cm

体积 (V) =?

我们知道圆柱体体积的公式

V= πr² h

将值代入上述公式，我们得到

V=3.14×(4.5²)×8
V=3.14×20.25×8
V=508.68

因此，圆柱体的体积为 508.68 cm³。

示例 4：圆柱体的体积为 255 cm³，高度为 15 cm。求圆柱体的半径 (r)。

解决方案

已知，体积 (V) = 255 cm³

高度 (h) = 15 cm

π = 3.14

半径 (r) =?

我们知道圆柱体体积的公式

V= πr² h

将值代入上述公式，我们得到

因此，圆柱体的半径为 2.3 厘米。

示例 5：计算空心圆柱体的体积。

解决方案

已知，外圆半径 (r₁) = 2.4 cm

内圆半径 (r₂) = 2 cm

高度 (h) = 10 cm

π = 3.14

体积 (V) =?

我们知道空心圆柱体体积的公式

将值代入上述公式，我们得到

V=3.14×10×(2.4^{2-22)
V=3.14×10×(5.76-4)
V=3.14×10×(1.76)
V=55.264}

因此，空心圆柱体的体积为 55.264 cm³。

示例 6：一根管道的外半径和内半径分别为 8 厘米和 6 厘米。管道的高度为 15 厘米。求管道的体积。取 pi=3.14。

解决方案

已知，外圆半径 (r₁) = 8 cm

内圆半径 (r₂) = 6 cm

高度 (h) = 15 cm

π = 3.14

体积 (V) =?

我们知道空心圆柱体体积的公式

将值代入上述公式，我们得到

V=3.14×15×(8²-6²)
V=3.14×15×(64-36)
V=3.14×15×2
V=1318.8

因此，空心圆柱体的体积为 1318.8 cm³。