体积公式

在几何学中，三维形状是具有三个维度的实体。这些维度包括物体的长度、宽度和高度。一些三维形状的例子有立方体、圆锥体、圆柱体、金字塔、球体等。我们计算这些形状的体积，以便测量物体在储存液体、气体等方面所占用的空间。不同形状有不同的体积公式。通过使用这些公式，我们可以计算出形状的体积。

在本节中，我们将学习所有三维形状的体积公式。

体积

物体所占据的空间量称为该物体的体积，其中物体是三维物体。我们计算体积以测量物体或容器的容量。我们可以通过使用公式轻松地计算任何三维形状的体积。如果三维形状很复杂，我们使用积分微积分来计算体积。

体积用字母 V 表示。我们以立方单位或单位³测量体积。在下表中，我们总结了所有体积公式，并附有图示以便更好地理解。

形状	Figure	体积公式	变量	Constant
立方体		V=a3 已知直径时	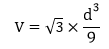a: 边长 d: 直径长度	-
圆锥体		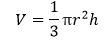已知斜高时	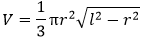r: 半径 h: 垂直高度 l: 斜高	π: 常数，其值为 3.14 或 22/7
圆柱体		V=πr2 h	r: 半径 h: 高度	π: 常数，其值为 3.14 或 22/7
空心圆柱体		V=πh(r22-r12)	r1: 内半径 r2: 外半径 h: 圆柱体的高度 D: 外径 d: 内径	π: 常数，其值为 3.14 或 22/7
长方体		V=长×宽×高	l: 长度 w: 宽度 h: 高度	-
球		已知直径时 已知周长时 已知面积时	r: 半径 d: 球体直径 C: 球体周长 A: 球体面积	π: 常数，其值为 3.14 或 22/7
半球			r: 半径	π: 常数，其值为 3.14 或 22/7
Pyramid		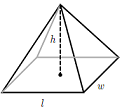	l: 底边长 w: 底边宽 h: 金字塔高度	-
长方棱柱		V=长×宽×高	l: 长度 w: 宽度 h: 高度	-
三棱柱			l: 长度 w: 宽度 h: 高度	-
椭球体			a, b, 和 c: 椭球体的半轴	π: 常数，其值为 3.14 或 22/7
四面体			a: 四面体的边	-