矩形面积

矩形是一个有四条边的多边形。矩形的性质是其对边的长度必须相等。我们可以使用包含高和宽的公式来求矩形的面积。

在本节中，我们将学习如何求矩形的面积，并将通过本节末尾给出的例子进行理解。

定义

矩形的面积是矩形在二维平面上覆盖的区域。换句话说，是宽度乘以高度。面积的单位是平方单位。

矩形面积公式

如果我们知道矩形的高度和长度，我们就可以计算出矩形的面积。

其中 w 代表宽度，h 代表高度。

有时我们已知矩形的对角线和宽度。然后我们应用以下公式来求矩形的面积。

矩形的性质

• 矩形的所有边都平行且相等。
• 每个直角都是 90° 度。
• 所有边长相等。
• 正方形总是矩形。

在上图中，红色边长度相同且相互平行。同样，绿色边长度相同且相互平行。矩形内的直角表示每个角度都是 90°。

示例

已知宽度和高度时

示例 1： 求高度为 5 米，宽度为 9 米的矩形面积。

解决方案

已知，h=5 米，w=9 米

我们知道：

矩形面积 (A) = 宽 * 高

将值代入上述公式，我们得到

矩形的面积是 45 米²。

已知对角线和宽度时

示例 2：求对角线长度为 20 厘米，宽度为 13 厘米的矩形板的面积。

解决方案

已知，对角线长度 (d) = 20，宽度为 13 厘米

我们知道：

矩形面积 (A) = 宽√对角线²-宽度²

A = 13 √20²-13²2

A = 13 √(400-169)

A = 13 √231

A = 13 * 15.19

A = 197.58 厘米²

矩形的面积是 197.58 厘米²。

使用勾股定理

示例 3：如果矩形 ABCD 的对角线是 100 厘米，其长度 x 是宽度 y 的两倍。求矩形的面积。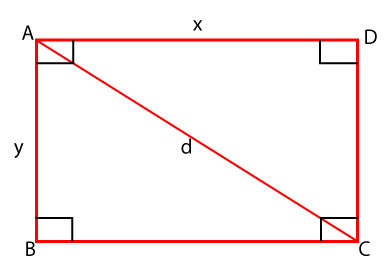

解决方案

已知，对角线 (d) = 100 厘米，宽度 (x)= 2y

根据勾股定理

斜边=√底边²+垂直边²

将值代入上述方程，我们得到

100²= y² + (2y)²

100²= y² + 4y²

100²= 5y²

解上述方程，

y=20√5

将 y 值代入宽度，我们得到
x = 40√5 厘米。

我们知道，

三角形面积 (A) = 宽 * 高

由于，

A = 40√5 厘米²

矩形的面积是 40√5 厘米²。