立方体体积

在本节中，我们将学习立方体的体积公式以及如何计算立方体的体积。

立方体是一种三维实体形状，其长、宽、高相等。它有六个正方形面。立方体的每个面都有等长的边。骰子是立方体的最佳示例。下图显示了立方体的形状。

• 边：连接两个顶点的线段称为边。立方体总共有十二条边。这些边长度相等。
• 面：面是立方体的正方形侧面。立方体总共有六个面（上、下、右、左、前、后）。
• 顶点：三条边相交的点称为顶点。立方体总共有八个顶点。

立方体的体积

立方体所占据的立方单位数量称为立方体的体积。它是长、宽、高的乘积。换句话说，它是一条边的立方。它用字母V表示。

立方体体积的公式

将长（l）、宽（b）和高（h）相乘即可得到立方体的体积。请记住，长、宽、高必须相等。

或

假设立方体的长、宽、高为a，则体积为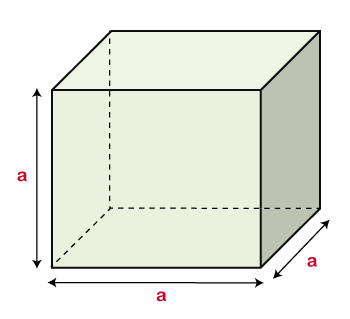

或

其中

V：是体积

a：是立方体的一条边

当给出对角线长度时

假设对角线长度为 d，则立方体的体积为

其中

V：是体积

d：是对角线长度

公式推导

固体物体所占据的空间称为该物体的体积。我们知道立方体中所有边（棱）的长度都相等。因此，立方体体积的公式可以推导如下：

• 取一块正方形纸板。
• 通过将长和宽相乘来计算该纸板的面积。
• 由于我们取的是一块正方形纸板，这意味着长和宽相等。假设长和宽为 a，则纸板的表面积将为a²。
• 为了获得立方体形状，我们将在该纸板上堆叠多块纸板，一块叠在另一块上。现在，我们可以计算立方体的高度。
• 要获得立方体的体积，请将纸板的表面积乘以高度。
• 从以上步骤可以看出，立方体所覆盖的面积是正方形表面积与高度的乘积。

让我们看看如何计算立方体的体积。

示例 1：立方体的一条边长为 9 厘米。计算立方体的体积。

解决方案

已知，边长 = 9 厘米

体积 (V)=?

根据公式

将边长的值代入上述公式，我们得到

V= 9³
V= 729

因此，立方体的体积为 729 cm³。

示例 2：礼品盒的对角线长度为 7 厘米。计算该盒子的体积。

解决方案

已知，对角线长度 (d) = 7 厘米

体积 (V) =?

根据公式

将 d 的值代入上述公式，我们得到

因此，立方体的体积为 66 cm³。

示例 3：骰子的体积为 64 cm³。计算骰子的棱长。

解决方案

已知，体积 (V) = 64 cm³

边长 (a)=?

根据公式

将边长的值代入上述公式，我们得到

64= a³
∛64= a
a=4

因此，骰子的棱长为 4 厘米。

示例 4：计算下方所示立方体的体积。

解决方案

已知，边长 (a) = 4.5 厘米

体积 (V)=?

根据公式

将边长的值代入上述公式，我们得到

V = (4.5)³
V = 91.125≈91.13

因此，给定立方体的体积为 91.13 cm³。