Borůvka 算法 - 最小生成树

在本教程中，我们将学习 Python 中的 Boruvka 算法。它用于识别最小生成树。捷克数学家 Otakar Boruvka 引入了此算法，并以其在图论方面的工作而闻名。此算法是图论中寻找最小生成树最著名的应用。我们将使用 Python 编程语言实现此算法。

它是最古老的最小生成树算法之一。根据记录，Boruvka 算法于 1926 年提出。它作为一种构建高效电网的方法发表。

在深入了解 Boruvka 算法并使用 Python 实现它之前，让我们先了解最小生成树的概念并回顾一下图。

图和最小生成树

图是一种抽象结构，表示一组称为节点（顶点）的几个对象。如果两个节点连接，则每个连接都称为边。

图用于解决现实生活中的问题，例如社交网络图和神经网络。如果简化图，我们可以绘制家谱或解释一些复杂的关系。

图的类型

图主要分为两种不同的类别：

• 无向图
• 有向图

无向图

无向图是指边没有方向的图。因此，无向图中的所有边都被认为是双向的。

我们将无向图定义为 G = (V, E)，其中 V 表示节点集，E 是一个包含来自 E 的无序元素对的集合，即边。

换句话说，无向图可以解释为我们无法定义边的方向，或者两个节点之间的关系总是双向的。例如，如果一条边从 A 到 B，则也有一条边从 B 到 A。

有向图

有向图是指边具有特定方向的图。我们将无向图定义为 G = (V, E)，其中 V 表示节点集，E 是一个包含来自 E 的有序元素对的集合，即边。

有序对意味着两条边之间的关系可以是单向的。换句话说，如果一条边从 A 到 B，我们无法确定是否存在一条边从 B 到 A。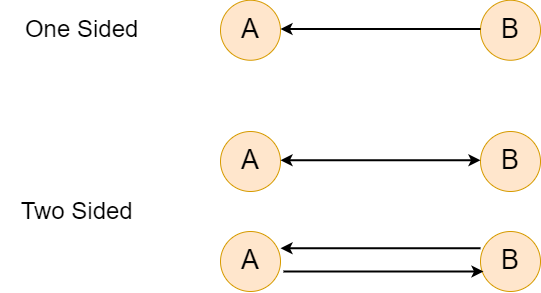

我们还可以根据边的权重对图进行分类。这些类型的图是加权图。

• 无权图

加权图

如果为边分配了一个数字，则该图是加权的。这些数字表示边的权重，即节点之间的权重、容量等。我们可以根据我们的问题来指代任何事物的权重。

加权图用于解决许多问题，例如需要找到最短路径，我们将在下一节中看到。

无权图

它与加权图正好相反；此类图的边上没有权重，并且图也可以是断开连接和连接的。

图也可以是连接的和断开连接的。如果两个节点之间存在路径，则将其视为连接图。另一方面，如果两个节点之间没有路径，则将其视为断开连接的图。

什么是树和最小生成树？

树是一种非线性、分层、无向图，其中两个边之间恰好存在一条路径，不多不少。子图是由A的节点和边的子集组成的图。

图 A 的生成树是图 A 的子图，它是一个树，其节点集与图 A 的节点集相同。

最小生成树是所有边的权重之和尽可能小的生成树。这里要记住的一点是，树不应该形成循环。

现在，让我们了解 Boruvka 算法

Boruvka 算法

Boruvka 算法直接而直观。它是一种贪婪算法，通过使用较小局部最优解来解决较小的子问题，从而构建全局“最优”解。

贪婪算法通常关注当较小的步骤累加时最优化解决方案。

让我们将算法分解为几个步骤

1. 以连通、加权和无向图作为输入。
2. 将所有节点初始化为单个组件。
3. 初始化空图最小生成树（MST）。它将包含解决方案。
4. 如果存在多个组件，则执行以下操作。
   • 找到连接此顶点与任何其他顶点的最小加权边。
   • 如果不存在，则将权重最小的边添加到 MST。
5. 如果只剩一个顶点，则返回最小生成树。

让我们以一个图为例，使用Boruvka 算法找到最小生成树。

在上面的无向图中，我们有九个顶点。现在让我们看下表中的加权分布。

现在我们的图将如下图所示 -

突出显示的线条显示了相互连接的最近顶点。正如我们所看到的，现在我们有组件：{0, 1}、{2, 4, 6, 7, 8}和{3, 5}。我们再次应用该算法来尝试找到最小权重边。

现在我们的图将如下图所示 -

正如我们所观察到的，图中只有一个顶点，表示最小生成树。这棵树的权重是 29，这是我们把所有边的权重相加得到的。

所以我们已经了解了 Boruvka 算法的工作原理。现在我们将使用 Python 实现它。

实施

在本节中，我们将编写算法的代码。请看下面的代码。

代码 -

输出

{0: 1, 1: 1, 2: 2, 3: 3, 4: 4, 5: 5, 6: 6, 7: 7, 8: 8}
Added edge [0 - 1]
Added weight: 4

{0: 1, 1: 1, 2: 4, 3: 3, 4: 4, 5: 5, 6: 6, 7: 7, 8: 8}
Added edge [2 - 4]
Added weight: 2

{0: 1, 1: 1, 2: 4, 3: 5, 4: 4, 5: 5, 6: 6, 7: 7, 8: 8}
Added edge [3 - 5]
Added weight: 5

{0: 1, 1: 1, 2: 4, 3: 5, 4: 4, 5: 5, 6: 6, 7: 4, 8: 8}
Added edge [4 - 7]
Added weight: 1

{0: 1, 1: 1, 2: 4, 3: 5, 4: 4, 5: 5, 6: 4, 7: 4, 8: 8}
Added edge [6 - 7]
Added weight: 1

{0: 1, 1: 1, 2: 4, 3: 5, 4: 4, 5: 5, 6: 4, 7: 4, 8: 4}
Added edge [7 - 8]
Added weight: 3

{0: 4, 1: 4, 2: 4, 3: 5, 4: 4, 5: 5, 6: 4, 7: 4, 8: 4}
Added edge [0 - 6]
Added weight: 7

{0: 4, 1: 4, 2: 4, 3: 4, 4: 4, 5: 4, 6: 4, 7: 4, 8: 4}
Added edge [2 - 3]
Added weight: 6
----------------------------------
The total weight of the minimal spanning tree is: 29

解释 -

在上面的代码中，我们创建了一个名为 Graph 的类，它包含了整个程序中使用的数据结构。在构造函数中，我们传递了 num_of_nodes 作为参数并声明了三个字段。

• m_v - 它表示图中节点的数量。
• m_edges - 它表示边的列表。
• m_vertex - 它是一个字典，用于存储节点所属顶点的索引。

我们定义了函数 add_edge(self, u, v, weight) 来将边添加到图中。函数 add_edge(self, u, v, weight) 将格式为 [first, second, edge_weight] 的边添加到我们的图中。然后，我们定义了 find_vertex() 和 set_vertex() 方法。在此方法中，我们将字典视为树。我们找到了组件的根。如果我们找不到根节点，我们递归地搜索当前节点的父节点。

union(self, vertex_size, u, v) 函数用于将两个组件统一为一个，给定属于各自组件的两个节点。然后，我们根据大小比较组件，并将较小的组件连接到较大的组件。然后，我们将较小组件的大小添加到较大组件的大小，因为它们具有相同的组件。

然后我们实现了 Boruvka 算法。

示例 -

在此方法中，我们初始化了 Boruvka 算法的组件列表。我们创建了一个列表来跟踪它们的大小，初始化为 1，以及一个最小权重边列表。

然后，我们找到连接该边的两端的组件的根节点。现在使用 if 条件，我们寻找连接这两个组件的最小边。

• 如果组件 u 的当前最小权重边不存在，我们则将我们正在监控的边的值分配给源的最小权重边。
• 如果组件 v 的当前最小权重边不存在，我们则将我们正在监控的边的值分配给目的地的最小权重。

在找到每个组件的最小权重边后，我们将它们添加到最小生成树中，并相应地减少组件的数量。

此算法的时间复杂度为 O(ElogV)，其中 E 表示边的数量，V 表示节点的数量。此算法的空间复杂度为 O(V+E)。

结论

还有许多其他流行的最小生成树算法，如 Prim 算法或 Kruskal 算法。然而，Boruvka 算法并不是一个众所周知的不同算法。它给出了几乎相同的结果——它们都找到了最小生成树，并且时间复杂度大致相同。

Boruvka 算法比其他算法提供更多优势；它不需要预先排序边或维护优先级队列来找到最小生成树。在本教程中，我们讨论了 Boruvka 算法、图和类型。