Python 中的用户定义数据结构

用户自定义数据结构在 Python 中不是内置的，但我们仍然可以实现它们。我们可以使用 Python 中现有的功能选项来创建新的数据结构。例如，当我们说 `list = []` 时，Python 就会将其识别为一个列表并调用所有与列表相关的操作。但是，当我们说“链表”或“队列”时，Python 就不知道这些是什么。在本文中，我们将讨论 Python 中的一些用户自定义数据结构。

1. 链表

链表，顾名思义，是相互连接的。链表中的每个节点都包含两个部分：数据字段，存储数据/值；以及 next 字段，存储指向下一个节点的引用，从而将它们连接起来。它是一个线性数据结构，但元素不存储在连续的内存位置。

链表的重要特点

1. 链表是元素的有序集合。
2. 链表也用于实现其他用户自定义数据结构，如栈和队列。
3. 使用 Python 中的 collections 模块，我们可以使用 deque 对象来实现链表上的插入和删除等操作。
4. 链表中的第一个节点是头节点，我们必须从它开始所有链表操作。
5. 链表的最后一个节点指向 None，表示链表已完成。

此外，链表有三种类型

1. 单链表
2. 双链表
3. 循环链表

一个简单的链表看起来像这样

如上图所示，头节点是第一个节点，最后一个节点的下一个（引用）部分保存 None。

双链表看起来像这样

在双链表中，每个节点将有三个部分。头节点保存第一个节点的引用，第一个节点的“前一个”部分保存 None，最后一个节点的 next 字段指向 None。每个节点将保存两个引用以及数据，一个指向其前一个节点，下一个指向其后一个节点。

循环链表

循环链表可以是单向的也可以是双向的

循环单链表

它是一个单链表，但列表中的最后一个节点保存第一个节点的引用，形成一个环。

循环双链表

它是一个双链表，但列表中的最后一个节点保存第一个节点的引用，第一个节点的“前一个”部分保存最后一个节点的引用，形成一个环。

示例程序

输出

Displaying the linked list:  10 -> 20 -> 30 -> None
Traversing from node to node:
10
20
30
After inserting 5 at the beginning: 5 -> 10 -> 20 -> 30 -> None
After inserting 40 at the end: 5 -> 10 -> 20 -> 30 -> 40 -> None
After inserting a node after 15: 5 -> 10 -> 15 -> 20 -> 30 -> 40 -> None
After inserting a node before 30: 5 -> 10 -> 15 -> 20 -> 25 -> 30 -> 40 -> None

2. 栈

栈是一种线性数据结构。它基于“LIFO”原则实现：后进先出。这意味着最后插入栈的元素将是第一个被删除的元素。栈只有一个开口，这意味着要插入或删除元素，我们需要使用同一端。当我们向栈中插入元素时，我们将元素一个接一个地插入——新元素在现有元素之上。插入所有元素后，如果我们要从栈中删除元素，最后插入的元素将是第一个出来的。

术语

1. 向栈中插入元素：push
2. 从栈中删除元素：pop
3. 栈的末端/开口：栈顶

Python 中用于栈的函数

栈的实现

我们可以实现一个栈

1. 使用列表
2. 使用链表
3. 使用 deque
4. 使用队列

输出

The elements of the stack
1
2
3
The first element to come out: 3
The second element to come out: 2
Final stack: [1]

• 使用列表的实现是最简单的。要将元素推入栈中，我们使用 list 的 append() 方法，要弹出元素，我们使用 stack 的 pop()

输出

Stack without pushing any elements: head None
Stack after pushing elements:
 head 14 13 12 11 10 None
After pop 3 times:
14
13
12
Stack:
 head 11 10 None
Element at the top of the stack:
11
Pop till stack becomes empty:
11
10
Traceback (most recent call last):
  File "D:\Programs\DSA \Language\Python data structures programs\stacks.py", line 59, in 
    print(mystack.pop())
  File "D:\Programs\DSA\Language\Python data structures programs\stacks.py", line 34, in pop
    raise Exception("Empty stack")
Exception: Empty stack

我们编写了两个方法 push 和 pop 来实现一个栈。我们需要确保两点

1. 执行 push 时，我们应始终将元素添加到链表的开头。
2. 执行 pop 时，必须删除开头的元素。
3. 我们创建了 size() 和 isEmpty()，以及 top() 来检查栈是否为空，因为如果栈为空，我们就无法执行 pop 操作。

3. 队列

队列是一种线性数据结构，类似于栈，但队列的实现原则是 FIFO - 先进先出。这意味着第一个插入队列的元素将是第一个从队列中出来的元素。

关于队列的重要事项

1. 队列将有两端——前端和后端。
2. 元素从前端插入，从后端删除。

术语

1. 将元素插入队列：入队 (enqueue)
2. 从队列中删除元素：出队 (dequeue)
3. 开头的元素：队头 (front)
4. 末尾的元素：队尾 (rear)

我们可以在 Python 中实现一个队列

1. 使用列表
2. 使用 collections 模块
3. 使用 queue.Queue

输出

Using lists:
Queue:  []
Inserting elements:
Queue: [1, 2, 3, 4, 5]
Deleting two elements:
Final queue: [3, 4, 5]

Using the deque class in the collection module
Inserting elements:
Queue: deque([6, 7, 8, 9, 10])
Deleting elements:
Final queue: deque([8, 9, 10])

Using the Queue class in the queue module
Inserting elements:
Queue:
0 1 2 3 4 5 
Is the queue full? True
Deleting elements:
Final queue: [2, 3, 4, 5]
size of the queue: 4

• 所有不同模块中使用的内置 Python 方法如上所示
  
• 队列可以与现实生活中的排队联系起来。第一个排队的人先拿到电影票。

在某些高优先级情况下，无论顺序如何，我们都必须首先处理某些方面。对于这种情况，有一种队列类型：优先级队列。

队列和优先级队列的区别

实施

输出

Created Q: 3 2 19 90 11
Dequeue operation:
The element to be deleted: 90
Final Queue: 2 3 11 19

4. 二叉树

树是节点的层次表示。家谱是树的实时示例。每个节点只能有两个子节点。层次最高或最顶部的节点称为“根节点”。

关于二叉树的重要事项

1. 每个节点都可以有一个左子树和一个右子树。
2. 因此，二叉树中的一个节点有 3 个部分：数据、指向左子节点的引用和指向右子节点的引用。
3. 没有子节点的最低层次节点称为叶节点。
   
4. 树可以使用 2 种方法遍历
   1. DFS：按深度
   2. BFS：按广度（或）层次
5. DFS 遍历又分为三种类型
   1. 前序遍历：首先访问根节点，然后是左子树，最后是右子树。
   2. 后序遍历：首先访问左子树，然后是右子树，最后是根节点。
   3. 中序遍历：首先访问左子树，然后是根节点，最后是右子树。
6. BFS 遍历是指我们按层次访问树。
   

输出

Preorder traversal:
4 3 2 3 5 
Postorder traversal:
2 3 3 5 4 
Inorder traversal:
2 3 3 4 5
BFS traversal:
4 3 5 2 3

• 有一种二叉树叫做 BST 或二叉搜索树。二叉树必须通过三个条件才能成为 BST

1. 左子树中节点的值必须小于根节点的值。
2. 右子树中节点的值必须大于根节点的值。
3. 树中的每个子树也必须遵循 BST 属性。

这是一个 BST 的例子:

5. 图

简而言之，G = (V, E)。这里 V 代表顶点，E 代表边。图是一种非线性数据结构。它由由边连接的节点/顶点组成。顶点和边都必须是有限集。一条边可以表示为 (u, v)，其中 u 和 v 是边连接的两个顶点。

图可以是定向的或无定向的。在无定向图中，E = (u, v) 和 E = (v, u) 是相同的，而在定向图中，它们是不同的，因为方向很重要。因此，边表示为边连接的顶点的有序对。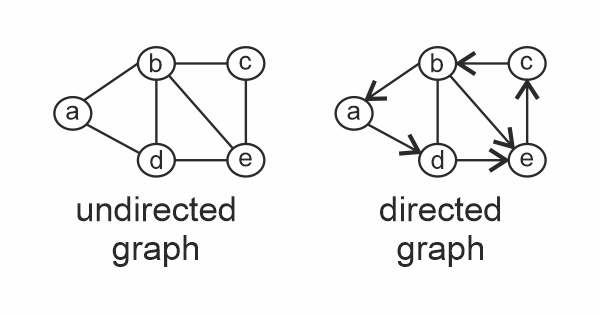

关于图的重要事项

1. 图的边可以有成本或权重。
2. 实时网络使用图表示。
3. 图可以使用以下方法实现
   1. 邻接矩阵
   2. 邻接表
   3. 邻接矩阵
   4. 邻接表
4. 程序员可以根据场景的需要选择如何实现图。
5. 图可以包含循环。
6. 对于图遍历，使用与树中相同的 BFS 和 DFS 技术，但为了避免在循环情况下反复访问同一个顶点，我们需要维护一个已访问顶点数组，以避免再次访问它们。

邻接矩阵：邻接矩阵是一个 (V X V) 二维数组，其中 V 代表图中的顶点。在矩阵 adj[u][v] 中，如果图中存在 u 和 v 之间的边，则 adj[u][v] = 1，否则赋值为 0。

• 在无向图中，如果存在从 u 到 v 的边，则 adj[u][v] = 1 且 adj[v][u] = 1，因为没有方向。因此，无向图的邻接矩阵总是对称的。
• 在有向图中，adj[u][v] 不等于 adj[v][u]。
• 如果边有权重或成本，则在矩阵中用指定的权重/成本替换 1。
• 这种表示法的缺点是占用空间更大 - O(V²)

这是表示方式

这是一个非常简单的图的邻接矩阵实现代码

输出

0 3 0 12 4 
3 0 5 0 0 
0 5 0 0 2 
12 0 0 0 7 
4 0 2 7 0

邻接表

为了实现邻接表，我们使用一个链表数组/列表来表示图中的顶点和边。表示中使用的链表数量等于图中顶点的数量。

• 创建一个长度等于顶点数的数组，对于每个顶点，我们创建一个包含所有相邻顶点的链表，并将这些链表排列在数组中。
• 在有向图的情况下，我们可以从数组中的节点遍历到的所有节点/顶点都链接在链表中。
• 简单来说，邻接表是一个链表数组，其中包含第一个节点的相邻节点。

这是表示方式

• 在上面的邻接表表示中，图是无向的。因此，图中每个节点的相邻节点都作为单独的链表链接。

• 这是一个有向图。因此，对于图中的每个节点，可以从该节点直接连接的相邻/邻近节点都被链接起来。
• 此外，图中每条边都给定成本。因此，成本也表示在链表中。

这是一个用邻接表表示图的简单代码

输出

0: -> 2 -> 1

1: -> 4 -> 2 -> 3 -> 0

2: -> 4 -> 1 -> 0

3: -> 4 -> 1

4: -> 2 -> 3 -> 1

理解

创建了一个大小等于图中顶点数的列表，所有值都为 None

[None, None, None, None, None]

现在，当调用 edge(源, 目标) 时

使用类节点创建一个目标节点，其下一个指向数组中的源，然后将链表分配给数组中的源位置。

当调用 edge(0, 1) 时

[1 -> None, 0 -> None, None, None, None]

edge(0, 2)

[2 -> 1 -> None, 0 -> None, 0 -> None, None, None]

edge(1, 3)

[2 -> 1 -> None, 3 -> 0 -> None, 0 -> None, 1 -> None, None]

这样，所有相邻节点都连接到数组中的链表。