使用 Python 介绍 Trie

2025年3月17日 | 阅读 15 分钟

一种名为 "Trie" 的树形信息结构，被描述为用于存储字符串集合并对其进行快速搜索。名称 "Trie" 来自于动词 "Retrieval"（检索），意指查找或获取某物的行为。

Trie 遵循一个规则，即如果两个字符串共享一个前缀，那么它们在 Trie 中将拥有相同的祖先。Trie 可以用来查找 Trie 中是否存在具有特定前缀的字符串，也可以用来按字母顺序对字符串集合进行排序。

为什么需要 Trie 数据结构？

Trie 数据结构用于数据存储和检索；类似的操作也可以使用哈希表数据结构来完成。然而，Trie 在执行这些任务时更有效。此外，Trie 相比哈希表有其自身的优势。基于前缀的查找可以使用 Trie 数据结构完成，而使用哈希表则不可能实现。

Trie 的基本结构是一种树状排列，其中每个节点代表一个字符串的单个字母或部分。从代表空字符串的根节点开始，当您沿着树向下移动时，字符被添加以创建完整的单词或短语。这种分层组织使得基于字符串的操作能够快速准确地进行。

Trie 的一个显著特点是其能够快速完成诸如查找具有相同前缀的单词或识别字典中满足特定模式的所有术语等任务。这些操作的时间复杂度取决于查询字符串的长度，而不是数据集的大小，这使得 Trie 在处理需要大量字符串集合的任务时非常高效。

此外，Trie 还用于字典和自动完成功能，这在聊天平台、代码编辑器和搜索引擎等应用程序中增强了用户体验。它们高效的前缀匹配能力可以实现实时建议，提高了用户交互的可用性和效率。

Trie 还有其他类型，如常规 Trie、压缩 Trie 和三叉搜索树，每种类型都旨在优化特定的用例。例如，压缩 Trie 通过合并共同前缀来最小化空间复杂度，而三叉搜索树则非常擅长有效管理大型词汇表。

Trie 有许多应用，包括 IP 路由、拼写检查和自然语言处理。理解 Trie 对于提高文本相关计算的速度和准确性以及优化基于字符串的算法仍然至关重要。

总而言之，Trie 是一种至关重要的数据结构，它能实现高效的基于字符串的操作。由于其在各种应用中的适应性和速度，它们提高了依赖于字符串匹配、搜索和索引的系统的性能。在不断扩展的计算机科学和信息技术领域，掌握 Trie 对于利用其强大功能和优化文本相关任务的算法至关重要。

Trie 信息结构相比哈希表有几个优势。

Trie 信息结构在以下方面优于哈希表

Trie 允许高效的前缀搜索（或自动完成）。
我们可以轻松地按字母顺序打印每个单词，而这对于哈希来说很困难。
在 Trie 信息结构中，没有哈希函数的开销。
即使在 Trie 信息结构中有大量的字符串集合，搜索一个字符串也只需要 O(L) 的时间复杂度，其中 L 是搜索词中的单词数。如果查询字符串不包含在 Trie 中，搜索时间甚至可能小于 O(L)。

Trie 数据结构的属性

我们知道 Trie 的组织结构像一棵树。因此，了解其特性至关重要。

下面列出了 Trie 信息结构的一些关键特性

因此，每个节点需要 26 个指针，其中第 0 个索引表示字母 "a"，第 25 个索引表示字符 "z"。
从根节点到特定节点的每条路径都代表一个单词或字符串。
这是一个直接的 Trie 信息结构模型。
每个 Trie 包含一个单一的根节点。
Trie 的节点对应于字符串，而其边对应于字符。
每个节点包含一个哈希映射或一个指针数组，其中每个索引是一个字符，并有一个标志表示该节点是否是任何字符串的结尾。
Trie 信息结构中可以使用任何数量的字符，包括字母、数字和特殊字符。但是，这里我们将专注于包含字母 a 到 z 的字符串。

Trie 信息设计

Trie 数据结构是如何工作的？

我们知道，Trie 信息结构中可以使用任何数量的字符，包括字母、数字和特殊字符。但是，这里我们将专注于包含字母 a 到 z 的字符串。因此，每个节点需要 26 个指针，其中第 0 个索引表示字母 "a"，第 25 个索引表示字符 "z"。

任何小写英文单词都可能以从头到尾的字母之一开始，然后是单词的第三个字母，同样是从 a 到 z 的字母之一，依此类推。为了存储一个单词，我们必须使用一个大小为 26 的数组（容器）。由于一开始没有单词，数组中的字符都是空的，如下所示。

让我们看看 Trie 数据结构如何存储 "and" 和 "ant" 这两个词

1. 在 Trie 数据结构中存储 "and"

因为 "and" 以 "a" 开头，我们将在 Trie 节点中将 "a" 的位置标记为已填充，表示使用了 "a"。
插入第一个字符后，第二个字符有 26 种选择，这意味着 "a" 本身又有一个 26 个字符的数组用于存储第二个字符。
因为 "n" 是第二个字符，我们将从 "a" 移动到 "n"，并在第二个数组中将 "n" 标记为已使用。
将相应数组中的 "d" 位置标记为已使用，因为 "d" 作为第三个字符跟在 "n" 后面。

2. 在 Trie 数据结构中存储 "ant"

根节点已经有了一个 "a"，因为单词 "ant" 以该字母开头。因此，没有必要再次填充它；只需移动到 Trie 节点 'a'。
对于第二个字符 'n'，我们可以看到 'a' 节点中 'n' 的空间已经被占用。所以不需要再次填充它；只需移动到 Trie 节点 'n'。
对于单词的最后一个字符 't'，'n' 节点中的 't' 插槽是空的。要前进到 't' 节点，请填充 'n' 节点中 't' 的位置。

存储 "and" 和 "ant" 这两个词后，Trie 将如下所示

Trie 节点的表示

每个 Trie 节点包含一个字符指针数组或哈希映射，以及一个标志，指示单词是否在该节点结束。但如果单词只包含小写字母（即 a-z），我们可以使用数组来创建 Trie 节点，而不是使用哈希映射。

# Python code
class TrieNode:
    # Trie node class
    def _init_(self):
        self.children = [None for _ in range(26)]
        # The amount of strings that are
        # stored in the Trie from the root node to any Trie node will be tracked by this.
        self.wordCount = 0 

Trie 数据结构的基本操作

插入
搜索
删除

1. Trie 数据结构的插入操作

此操作将新字符串添加到 Trie 数据结构中。让我们先测试一下这个

让我们尝试在这句话中添加 "and" 和 "ant"

在上面显示的插入表示中，单词 "and" 和 "ant" 有一个共同的节点（即 "an"）。这是由于 Trie 数据结构的特性，即如果两个字符串共享一个前缀，它们将有相同的祖先。

现在让我们尝试插入 "dad" 和 "do"

在 Trie 数据结构中实现插入

算法

创建函数 `embed (TrieNode *root, string &word)`，它将接受两个参数：根节点和要插入到 Trie 数据结构中的字符串。
然后，用根节点初始化一个名为 currentNode 的新指针。
当你遍历给定字符串的长度时，检查指针数组中当前字符位置的值是否为无效。
- 如果它是无效的，创建一个新节点，并将当前字符指向这个新节点。
- 将 curr 移动到全新的节点。
然后应增加最后一个 currentNode 的单词计数，表明 currentNode 是一个字符串的结尾。

以下是上述算法的执行过程

def insert_key(root, key):
    # Set the root node as the current node pointer's initial value.    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify the existence of the Node for the current
        # the Trie character.
        if currentNode.childNode[ord(c) - or('a')] == None:
            # If the Node for the current character is missing, create a new node.
            newNode = TrieNode()
            # Keep the reference for the 
            # node that was just formed.
            currentNode.childNode[ord(c) - ord('a')] = newNode
        # Transfer the current node pointer to the newly generated Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    # WordEndCount for the most recent current Node is increased.
    # pointer This suggests that a string with an ending of 
   # currentNode exists.
    currentNode.wordCount += 1

2. Trie 数据结构搜索

搜索操作与 Trie 中的插入操作唯一的不同之处在于，每当我们发现 curr 节点中的指针数组不指向单词的当前字符时，我们返回 false，而不是为该字符创建一个新节点。

使用此策略，您可以检查一个字符串是否存储在 Trie 信息结构中。Trie 信息结构有两种不同的搜索技术。

检查 Trie 以查看提供的单词是否存在。
检查 Trie 以查看是否存在任何具有指定前缀的单词。

这两种方法都使用类似的研究模式。将一个单词完全转换为字母，并将每个字母与从根节点开始的 trie 节点进行比较，是 Trie 查找给定单词的初始步骤。如果找到了当前字符，则继续到该节点的子节点。持续这样做，直到找到所有字符。

2.1 Trie 数据结构前缀搜索：在 Trie 数据结构中查找前缀 "an"。

Trie 数据结构中的前缀搜索实现

def is_prefix_exist(root, key):
    # Set the root node as the current node pointer's initial value.
    current_node = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the current 
        # character in the Trie exists.
        if current_node.child_node[ord(c) - or('a')] is None:
            # There isn't a given word prefix in Trie.
            return False
        # Transfer the currentNode reference to the current character's 
       # existing Node.
        current_node = current_node.child_node[ord(c) - or('a')]
  # Prefix exists in the Trie
    return True

2.2 在 Trie 数据结构中进行完整单词搜索

这与前缀搜索类似，但我们还必须确定单词是否在最后一个字符处结束。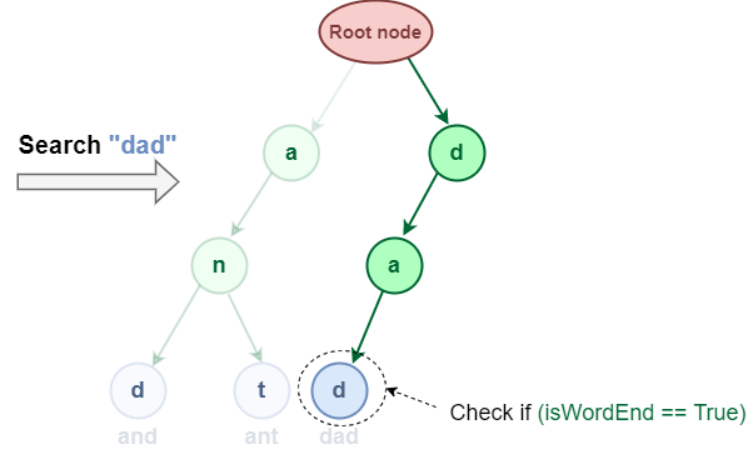

使用搜索算法与 Trie 数据结构

def search_key(root, key):
    # Set the root node as the current node pointer's initial value.
    currentNode = root  
    # iterate over the string's length
    for c in key:
        # Verify if there is a node for the character you see in the Trie.
        if currentNode.childNode[ord(c) - or('a')] is None:
            # In Trie, the given word doesn't exist.
            return False
  
        # Transfer the current node reference to the current character's existing Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]  
    # If the word count is more than 0, return it.
    return currentNode.wordCount > 0

3. Trie 数据结构删除

字符串可以使用此方法从 Trie 数据结构中删除。从 Trie 中删除一个单词时，有三种情况。

被删除的单词是 Trie 中其他单词的前缀。
被删除的单词与 Trie 中的其他单词有共同的前缀。
被删除的单词与 Trie 中的其他单词没有共同的前缀。

示例

3.1 被删除的单词是其他 Trie 单词的前缀。

如附图所示，被删除的单词 "an" 与单词 "and" 和 "ant" 共享一个完整的前缀。

在这种情况下，通过在单词结束节点处将单词计数减 1 来执行删除操作。

3.2 被删除的单词与 Trie 中的其他单词有共同的前缀。

如附图所示，被删除的词 "and" 有几个前缀，与以 "ant" 开头的其他词相同。它们都以 "an" 开头。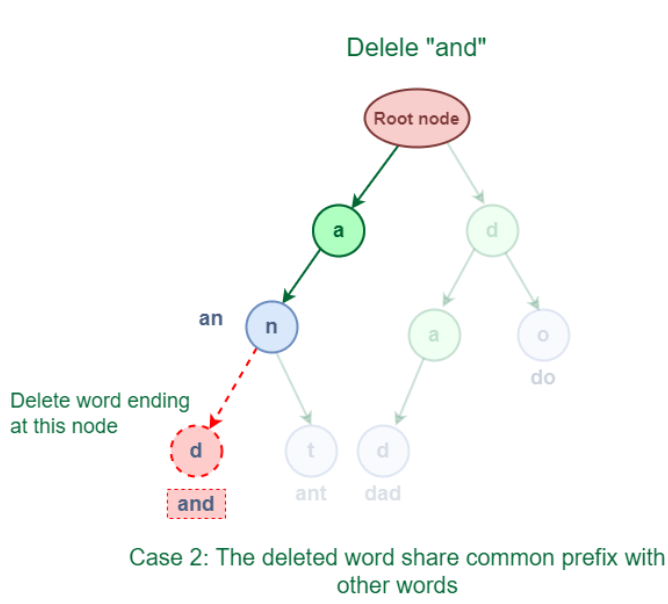

3.3 被删除的单词与任何其他 Trie 术语没有共同的前缀。

如附图所示，术语 "java" 与任何其他单词没有共同的前缀。

在这种情况下，只需删除每个节点即可解决问题。

下面显示了处理上述所有情况的实现

def delete_key(root, word):
    current_node = root
    last_branch_node = None
    last_branch_char = 'a' 
    # iterate over each letter in the word
    for c in word:
        # Unless the current character is a child of the current Node,
        # Because the term is absent from Trie, return False.
        if current_node.childNode[ord(c) - or('a')] is None:
            return False
        else:
            count = 0
            # count how many offspring the current Node has.
            for i in range(26):
                if current_node.childNode[i] is not None:
                    count += 1
            # save the Node and the current character if the number of children exceeds 1.
            if count > 1:
                last_branch_node = current_node
                last_branch_char = c
              current_node = current_node.childNode[ord(c) - or('a')]
      count = 0
    # count how many offspring the current Node has.
    for i in range(26):
        if current_node.childNode[i] is not None:
            count += 1  
    # Case 1: The removed word functions as a prefix for other Trie words.
    if count > 0:
        current_node.wordCount -= 1
        return True 
    # Case 2: The eliminated word has a prefix in common with other words in Trie.
    if last_branch_node is None:
        last_branch_node.childNode[ord(last_branch_char) - ord('a')] = None
        return True
    # Case 3: Trie has no common prefix between the removed word and any other words.
    else:
        root.childNode[ord(word[0]) - or('a')] = None
        return True

Trie 数据结构是如何实现的？

使用 TrieNode() 构造函数创建一个根节点。
将一组字符串保存在一个名为 arr 的字符串向量中，我们将用它来将字符串放入 Trie。
使用 insert_key() 方法将每个字符串插入到 Trie 中，
search_key() 方法可用于从搜索查询字符串中搜索字符串。
借助 delete_key，从 deleteQueryStrings 中删除字符串。

# Trie implementation in Python   
class TrieNode:
    def __init__(self):
        # pointer array for each Node's children
        self. child node = [None] * 26
        self.wordCount = 0          
def insert_key(root, key):
    # Set the root node as the current node pointer's initial value.
    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the selected character in the Trie exists.
        if not currentNode.childNode[ord(c) - or('a')]:
            # If there is no node for the current character
            # Then make a new node
            newNode = TrieNode()
            # Keep the Node's reference that was just formed.
            currentNode.childNode[ord(c) - ord('a')] = newNode
        # Transfer the current node pointer to the brand-new Node at this moment.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    # WordEndCount for the most recent currentNode is an increased pointer 
   # This suggests that currentNode has a string at its conclusion.
    currentNode.wordCount += 1
def search_key(root, key):
    # Set the root node as the currentNode pointer's initial value.
    currentNode = root
    # iterate over the string's length
    for c in key:
        # Verify if the Node for the selected character in the Trie exists.
        if not currentNode.childNode[ord(c) - or('a')]:
            # In Trie, the given word doesn't exist.
            return False
        # Transfer the currentNode reference to the current character's existing Node.
        currentNode = currentNode.childNode[ord(c) - or('a')]
    return currentNode.wordCount > 0 
def delete_key(root, word):
    currentNode = root
    lastBranchNode = None
    lastBrachChar = 'a'  
    for c in word:
        if not currentNode.childNode[ord(c) - ord('a')]:
            return False
        else:
            count = 0
            for i in range(26):
                if currentNode.childNode[i]:
                    count += 1
            if count > 1:
                lastBranchNode = currentNode
                lastBrachChar = c
            currentNode = currentNode.childNode[ord(c) - ord('a')]  
    count = 0
    for i in range(26):
        if currentNode.childNode[i]:
            count += 1  
    # Case 1: The deleted word functions as a prefix for other Trie words.
    if count > 0:
        currentNode.wordCount -= 1
        return True  
    # Case 2: The eliminated word has a prefix in common with other words in Trie.
    if lastBranchNode:
        lastBranchNode.childNode[ord(lastBrachChar) - ord('a')] = None
        return True
    # Case 3: There is no prefix that the removed word has in common with other words in Trie.
    else:
        root.childNode[ord(word[0]) - or('a')] = None
        return True
# Driver Code
if __name__ == '__main__':
    # Create a Trie root node.
    root = TrieNode() 
    # Contains the strings that we wish to add to the Trie.
    input_strings = ["and", "and", "do", "java", "dad", "ball"]
    # number of Trie insert procedures
    n = len(input_strings)
    for i in range(n):
        insert_key(root, input_strings[i])
    # stores the strings we wish to search for in the Trie database.
    search_query_strings = ["do", "java", "bat"]  
    # amount of searches conducted in Trie
    search_queries = len(search_query_strings)  
    for i in range(search_queries):
        print("Query String:", search_query_strings[i])
        if search_key(root, search_query_strings[i]):
            # The Trie contains the query string
            print("The query string is present in the Trie")
        else:
            # The Trie does not contain the query string.

            print("The query string is not present in the Trie")
    # saves the strings from the Trie that we wish to remove.
    delete_query_strings = ["java", "tea"]
    # amount of deletions made using the Trie
    delete_queries = len(delete_query_strings)
    for i in range(delete_queries):
        print("Query String:", delete_query_strings[i])
        if delete_key(root, delete_query_strings[i]):
            # The Trie successfully deletes the queryString.
            print("The query string is successfully deleted")
        else:
            # The Trie does not contain the query string.
            print("The query string is not present in the Trie")

输出

Query String: do
The query string is present in the Trie
Query String: java
The query string is present in the Trie
Query String: bat
The query string is not present in the Trie
Query String: java
The query string is successfully deleted
Query String: tea
The query string is not present in the Trie

Trie 数据结构复杂度分析

操作	时间复杂度	辅助空间
插入	O(n)	O(n*m)
搜索	O(n)	O(1)
删除	O(n)	O(1)

注意：在上面的复杂度图中，"n" 和 "m" 分别代表字符串长度和存储在 Trie 中的字符串数量。

Trie 数据结构的应用包括

1. 自动完成功能： 自动完成功能根据您输入的搜索词提供建议。自动完成功能是使用 trie 数据结构实现的。

2. 拼写检查器： 如果单词没有出现在字典中，它们会根据您输入的内容提供建议。

它有3个步骤，如下所示

在数据字典中搜索该术语。
提出可能的建议。
将建议按优先级更高者排在顶部。

Trie 保存字典数据，促进了字典术语搜索算法的开发，并提供了一个可接受的建议词列表。

3. 最长前缀匹配： 它通常被称为最长前缀匹配算法，是 IP 网络中使用的一种路由技术。连续掩码对于网络路由优化是必要的，它将搜索时间复杂度限制为 O(n)，其中 n 是 URL 地址的位数。

为了加快搜索过程，开发了多种位 Trie 方法，通过更快地进行多位查找来提速。

Trie 数据结构的优点

Trie 数据结构的优点包括其能够以 O(l) 的时间输入字符串并找到它们，其中 l 是单个单词的长度。与二叉搜索树和哈希表相比，它更快。
它通过节点键对条目进行字母顺序过滤，从而更容易按字母顺序打印所有单词。
Trie 需要的存储空间比 BST 少，因为每个键只需要预定量的摊销空间来存储，而不是明确记录。
trie 数据结构使得能够有效地执行前缀搜索和最长前缀匹配。
对于像整数和指针这样的短键，Trie 通常比哈希表更快，因为它们的实现不需要哈希函数。
Trie 允许有序迭代，但哈希表只允许伪随机迭代，这通常更费力，由哈希函数决定。
简单的删除算法的时间复杂度为 O(l)，其中 l 是要删除的单词的长度。

Trie 数据结构的缺点

trie 数据结构最大的缺点是它需要大量内存来存储所有字符串。我们每个节点都有过多的节点指针，在最坏的情况下，这等于字母的数量。
当哈希表构建得有效时（即，具有合适的哈希函数和可接受的负载因子），查找时间为 O(1)，这比 trie 的 O(l) 快得多，其中 l 是字符串的长度。

下一个主题在 BST 中使用常数额外空间查找第 K 大元素（使用 Python）

使用 Python 介绍 Trie

为什么需要 Trie 数据结构？

Trie 数据结构的属性

Trie 数据结构是如何工作的？

Trie 节点的表示

Trie 数据结构的基本操作

1. Trie 数据结构的插入操作

2. Trie 数据结构搜索

3. Trie 数据结构删除

Trie 数据结构是如何实现的？

Trie 数据结构复杂度分析

注意：在上面的复杂度图中，"n" 和 "m" 分别代表字符串长度和存储在 Trie 中的字符串数量。

Trie 数据结构的应用包括

Trie 数据结构的优点

Trie 数据结构的缺点

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Python 问题

使用 Python 介绍 Trie

为什么需要 Trie 数据结构？

Trie 数据结构的属性

Trie 数据结构是如何工作的？

Trie 节点的表示

Trie 数据结构的基本操作

1. Trie 数据结构的插入操作

2. Trie 数据结构搜索

3. Trie 数据结构删除

Trie 数据结构是如何实现的？

Trie 数据结构复杂度分析

注意：在上面的复杂度图中，"n" 和 "m" 分别代表字符串长度和存储在 Trie 中的字符串数量。

Trie 数据结构的应用包括

Trie 数据结构的优点

Trie 数据结构的缺点

相关帖子

Python 中的类和对象

如何在 Python 中创建 requirements.txt 文件

Python ChemPy 模块

Python 中的 Deque

Python 中有效的根搜索算法

Python wxPython 模块

Python AES CTR

Python 程序打印帕斯卡三角形

使用 CustomTkinter 模块在 Python 中创建现代登录 UI

Python 中的元字符

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器