使用 Python 解决物理计算问题

本文展示了如何利用 Python 和 Numpy 库解决简单的拉普拉斯方程，并使用 Matplotlib 绘制方程的解。我们还将看到，使用 Python 可以编写更少的代码并完成更多的工作。

呈现

拉普拉斯方程是一个简单的二阶偏微分方程。它也是椭圆偏微分方程最简单的例子。这个方程在科学中，尤其是在物理学中非常重要，因为它描述了电势和磁势以及热传导的行为。在热力学（热传导）中，我们将拉普拉斯方程称为稳态热或热传导方程。

在本文中，我们将使用数值方法而不是分析/微积分方法来求解拉普拉斯方程。当我们说数值方法时，我们指的是离散化。离散化是将微分方程的连续形式“转换”为微分方程的离散形式的过程；它也意味着通过离散化，我们可以将数学问题转换为矩阵多项式问题，这更倾向于编程。

在这里，我们必须使用有限差分法解决一个基本的热传导问题。我们将使用 Python 编程语言、Numpy（Python 的数值库）和 Matplotlib（用于使用 Python 绘制和可视化数据的库）作为工具。我们还将看到，使用 Python 可以编写更少的代码并完成更多的工作。

背景

在计算物理学中，我们“始终”使用编程来解决问题，因为计算机程序可以“快速”计算大量复杂的估计。计算物理学可以用这个图表来表示。

当今有许多编程语言用于解决许多数值问题，例如 Matlab。但是，在这里，我们将使用 Python，这种“易于学习”的编程语言，而且，它是免费的。它还拥有强大的数值、科学和数据可视化库，如 Numpy、Scipy 和 Matplotlib。Python 还提供并行执行，我们可以在计算机集群中运行它。

回到拉普拉斯方程，我们将在下一节中使用 Python 解决一个简单的二维热传导问题。在这里，我假设读者对有限差分法有基本了解，所以我不会详细介绍有限差分法、离散化误差、稳定性、一致性、组合和最快/最优迭代算法的细节。我们将跳过计算方程的许多步骤。

我们不使用数值、分析验证来解决问题，而是展示如何使用 Python、Numpy 和 Matplotlib 来解决问题，并带有计算物理学的一些简化感觉，因此这里的源代码对于不专攻计算物理学的普通读者来说是合乎情理的。

计算物理学的挑战

计算物理学问题通常很难精确解决。这是由于几个（数值）原因：缺乏对数或分析可行性、复杂性和混乱。例如，即使是看似简单的问题，例如计算围绕原子在强电场中运行的电子的波函数（独特效应），也可能需要付出巨大的努力来设计一个实用的算法（如果能找到的话）；可能需要其他粗糙或蛮力技术，例如图形方法或求根方法。

在更高级的方面，数值微扰理论有时也会被使用（此处显示了此特定模型的推导）。此外，对于大多数多体问题（及其传统对应物）来说，计算成本和复杂性往往会迅速增长。一个可见的系统通常具有大约 10²³ 个组成粒子的大小，因此这通常是一个问题。

解决量子力学问题通常在系统大小方面呈指数级增长 [5]，而对于经典 N 体问题，则呈 N 平方级增长。最后，许多物理系统本质上最多是非线性的，最坏情况下是混沌的：这意味着很难保证任何数值误差不会随着结果的产生而累积，从而使“解”无用。

方法和计算

由于计算材料物理学涉及广泛的问题类别，因此它根据其数值求解的不同数值问题或其应用的方法进行划分。其中，可以考虑

• 求根（例如，使用牛顿-拉夫逊法）
• 线性方程组（例如，使用 LU 分解）
• 常微分方程（例如，使用龙格-库塔法）
• 积分（例如，使用龙伯格法和蒙特卡罗积分）
• 偏微分方程（例如，使用有限差分法和松弛法）
• 矩阵特征值问题（例如，使用雅可比特征值算法和幂循环）

许多方法（以及其他一些方法）用于计算所建模系统的物理性质。

计算材料物理学也从计算化学中借鉴了许多思想。例如，计算固态物理学家用来计算固体性质的密度泛函理论与化学家用来计算粒子性质的理论基本相同。

此外，计算物理学还包括软件/硬件架构调整以解决问题（因为这些问题通常在处理能力需求或内存需求方面可能非常庞大）。

准备工作

为了生成以下结果，我使用了这个环境

• 操作系统：Linux Ubuntu 14.04 LTS
• Python：Python 2.7
• Numpy：Numpy 1.10.4
• Matplotlib：Matplotlib 1.5.1

如果您正在运行 Ubuntu，您可以使用 pip 安装 Numpy 和 Matplotlib，或者您可以在终端中运行此命令。

并使用此命令安装 Matplotlib

请注意，Python 目前已安装在 Ubuntu 14.04 中。要尝试 Python，请在终端中键入 Python 并按 Enter。

您也可以在 Windows 操作系统中使用 Python、Numpy 和 Matplotlib，但我更喜欢使用 Ubuntu。

使用公式

这是二维笛卡尔坐标系中的拉普拉斯方程（用于热方程）

其中 T 是温度，x 是 x 轴，y 是 y 轴。x 和 y 是笛卡尔坐标系中位置的函数。如果您有兴趣查看上述方程的解析解，您可以在此处找到。

在这里，我们必须解决拉普拉斯方程的二维形式。要解决的问题如下所示

我们将根据给定的边界条件（板边缘的温度）找到上述二维板内的稳态温度（这也意味着拉普拉斯方程的解）。然后，我们将对板的区域进行离散化，并将其划分为网格，然后，我们将使用有限差分法对上述拉普拉斯方程进行离散化。这是板的离散化区域。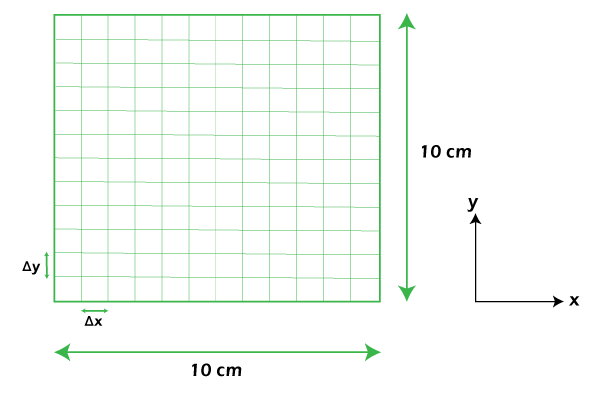

我们设置 Δx = Δy = 1 厘米，然后制作如下所示的网格

请注意，绿色节点是我们希望知道温度（解）的节点，白色节点是边界条件（已知温度）。这是上述拉普拉斯方程的离散形式。

在我们的情况下，最终的离散方程如下所示。

现在，我们准备好处理上面的条件。为了解决这个问题，我们使用内部矩阵（绿色节点）的“猜测值”；在这里，我们将其设置为 30 摄氏度（或者我们可以将其设置为 35 或其他值），因为我们不知道矩阵内部的值（显然，这些是我们希望知道的值）。

然后，我们将重复条件，直到循环前的值与循环后的值之间的差异“足够小”；我们称之为组合。在重复的过程中，内部矩阵中的温度值会自行改变；它是“自校正的”，因此当我们设置的假设值越接近真实解，我们获得“真实”解的速度就越快。

步骤 1： 我们已经准备好源代码。要使用 Numpy 库，我们需要在源代码中导入 Numpy，还需要导入 Matplotlib. Pyplot 模块来绘制我们的解决方案。所以，第一步是导入基本模块。 代码片段：

步骤 2： 之后，我们将初始变量设置到我们的 Python 源代码中。

代码片段

步骤 3： 接下来我们将设置“绘图窗口”和网格。这是代码。

代码片段

步骤 4： nps.meshgrid() 为我们创建网格（我们用它来绘制解决方案），第一个参数用于 x 轴，第二个参数用于 y 轴。我们使用 nps.arange() 来排列一个一维数组，其元素值从某个值开始到某个值；在我们的例子中，它从 0 到 lenXs，从 0 到 lenYs。

然后我们设置区域：我们定义二维数组，定义大小并用猜测值填充数组；然后，我们放下边界条件，并查看此处上述边界条件填充数组元素的语法。

代码片段

步骤 5： 然后，我们准备将最终条件应用于下面的 Python 代码。我们使用 for 循环重复条件。

代码片段

步骤 6： 您应该注意上面代码的空格；Python 不使用括号，而是使用空格或制表符。好的，主要逻辑已经完成。然后，我们编写代码，使用 Matplotlib 绘制解决方案。

代码片段

最终完整源代码。

很短，是吧？好的，您可以复制粘贴并保存源代码，将其命名为 findif.py。要执行 Python 源代码，请打开终端，转到源代码所在的目录，键入

并按回车键。然后会出现绘图窗口。

输出

您可以尝试更改边界条件的值；例如，如果您将右边缘温度的值更改为 30 摄氏度（Trights = 30），那么结果将如下所示

总结

Python 是一种“易于学习”且逐步编写的编程语言，它提供（开源）强大的计算物理学或其他科学学科库。由于 Python 是一种解释型语言，与 C 或 C++ 等编译型语言相比，它的速度较慢；但是，它再次易于学习。我们还可以使用 Python 编写更少的代码并完成更多的工作，因此我们不需要费力编程，而是专注于我们想要解决的问题。

在计算物理学中，借助 Numpy 和 Scipy（Python 的数值和科学库），我们可以解决许多复杂问题，因为它提供了矩阵求解器（特征值和特征向量求解器）、线性代数运算，以及信号处理、傅里叶变换、统计、优化等。

除了计算物理学，Python 还用于人工智能，甚至谷歌的 TensorFlow 也使用 Python。