Python 中的物理计算：Python 函数简介

你准备好用 Python 提升你的物理科学计算水平了吗？如果答案是肯定的，那么你需要掌握 Python 函数。我们喜欢物理科学和 Python，但这并不意味着我们是专业的软件工程师；我们是普通人。

我将假设你已经用 Python 进行过一个数学计算。它不必是多么复杂的东西。也许只是一个没有空气阻力的抛射物运动。

好吧，但是，老天爷，什么是一个函数？

它与数学函数相同。类似这样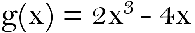

对于这个数学函数，你可以输入任何你想要的 x 值，它会“输出”一个值。Python 函数也可以是这样的。这可能是一个 Python 函数。看起来会是这样。

函数

• 是的，这可能是最无聊的 Python 程序了。但这是一个很好的起点。这里有一些重要的注意事项
• 函数需要一个独特的名字。我可以给它命名为“g”，只要没有其他函数或变量被命名为“g”即可。
• 你在定义中选择输入变量名（是的，你需要 `def` 部分和冒号）。在这种情况下，我使用了“x”，但只要你在函数体内使用相同的名称即可。
• 输出是 `return()` - 你放在括号里的任何东西都将是函数的输出。
• 这个函数有一个输入（x）和一个输出——但你可以拥有任意数量的输入和输出。

抛射物运动函数

再来一个可能有用的例子怎么样？我将创建一个函数，它接受一个物体的初始速度向量和离地面的高度。然后它返回“射程”——物体前进的水平距离。

虽然我可以用一个解析解来计算这个射程，但我将用数值方法来计算。作为快速回顾，以下是如何计算物体水平前进的距离。

• 从物体的初始位置和速度开始。我可以通过速度和质量找到物体的动量。
• 将运动分解成微小的增量。比如 0.01 秒？
• 计算物体的力。在这种情况下，它只是一个恒定的重力。
• 我们可以利用这个力以及当前动量来找到在完成短暂时间增量后的新动量。
• 最后，利用动量，我可以更新物体的位置。

继续这个循环，直到物体到达“地面”，我将其定义为 y1 = 0 米。

源代码

输出

初始速度、初始高度和垂直速度之间的关系可以用右侧的直角三角形来表示，其中 q（如下图所示）是抛射物离开水平面的点（通常是地面）。这一点就是发射角。

现在是注释

• 第一行，我将函数命名为 `xrange(v0, h, m)`。首先，我几乎可以肯定 `range` 已经是 glowscript（是的，我正在使用 glowscript）中加载的某个模块中的一个函数了。其次，我将三个参数传递给函数。看看，`v0` 是一个向量，我甚至不必声明它是那种类型。
• 第 13 行，带有进行数值计算的循环，就像一个完整的程序一样。
• 循环条件是直到位置不再大于零。因为我把位置定义为向量，所以 `r.y` 是该位置的 y 分量。
• 第 14、15、16 行都是向量方程。因为 `p` 是一个向量，所以右侧是一个向量运算。这难道不酷毙了吗？
• 第 18 行返回最终位置。这个函数返回的是位置的标量 x 分量。但你也可以把它定义为 `r`——也许你应该试试看会发生什么。
• 最后，在第 20 行和 21 行，我打印出函数对一组特定输入的输出。这是为了确保它正常工作。
• 现在我们来利用一下这个东西，好吗？我想找到能产生最大射程的发射角度。这是实现这一目标的代码。
• 它使用了与之前相同的函数（尽管我将时间步长从 0.01 更改为了 0.001）。现在还有一些注意事项
• 第 20-24 行只是初始条件。质量不改变，但我稍后会用到它。另外，用幅度和角度来比较发射速度更容易——但在调用函数之前，我将其转换为向量。
• 第 22 行是角度步长。我将对某个初始发射角度调用函数，然后对稍高一点的角度重复调用。
• 第 26-27 行只是用于准备图表。这是你的 Python 图表教程。
• 第 29-33 行是运行函数并使用不同发射角度的循环。这包括跟踪发射速度向量（第 30 行）和绘图（第 32 行）。

请注意，最大射程是在大约 36 度的发射角度实现的——而不是 45 度。请记住，当从水平地面发射到水平地面时，抛射物的最大射程是 45 度。在这种情况下，我让物体从离地面 1 米的高度发射。

是的，你可以使用一种有效得多的、更复杂的方法来打印出最大射程，但查看图表也足够了。