统计学中使用 Python 的 Lomax 分布17 Mar 2025 | 4 分钟阅读 scipy.stats.lomax 描述了Lomax连续随机变量。它是rv_continuous类的一个实例，继承自通用方法。它通过添加特定于此分布的细节来完善技术。 给出Lomax分布的概率密度函数如下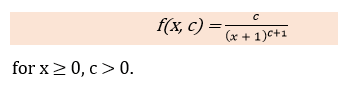：  定义的lomax分布的概率密度函数是标准化形式。我们使用loc和scale参数来移动和缩放分布。位置的移动并不会使其成为非中心分布。lomax.pdf(x, loc, scale) 等价于 lomax.pdf(y, c) / scale，其中 y = (x - loc) / scale。Lomax是Pareto分布的一个特例，loc值为1.0。 Lomax分布包含的参数
默认值为 'mv'（平均值和方差）
Python在scipy.stats库中提供了lomax模块，用于查找Lomax分布。 在Python中导入lomax()库让我们通过不同情况下的不同程序来理解统计学中Lomax分布的概念。 程序1：创建Lomax分布随机变量的程序 代码 输出 Random Variable : <scipy.stats._distn_infrastructure.rv_continuous_frozen object at 0x000001A778F72D50> 说明 使用lomax()函数，我们创建了一个Lomax分布随机变量。首先，我们导入了lomax模块，并将x和y两个变量赋值为随机值。然后使用lomax函数创建了随机变量。 程序2：创建Lomax连续变量及其概率分布的程序。 代码 输出 Random Variates : 4.3263639849502695 The Probability Distribution : [0.00652862 0.00663204 0.00673741 0.00684477 0.00695417 0.00706566 0.00717927 0.00729506 0.00741308 0.00753338 0.00765599 0.00778099 0.00790842 0.00803834 0.00817079 0.00830585 0.00844357 0.00858402 0.00872724 0.00887331 0.0090223 0.00917427 0.00932929 0.00948743 0.00964876 0.00981337 0.00998132 0.01015269 0.01032758 0.01050605 0.0106882 0.01087412 0.01106388 0.0112576 0.01145536 0.01165725 0.01186339 0.01207388 0.01228881 0.01250831 0.01273248 0.01296144 0.01319531 0.0134342 0.01367825 0.01392759 0.01418234 0.01444265 0.01470866 0.0149805 0.01525834 0.01554232 0.01583259 0.01612933 0.01643271 0.01674288 0.01706003 0.01738435 0.01771602 0.01805523 0.01840218 0.01875709 0.01912015 0.0194916 0.01987164 0.02026053 0.02065848 0.02106576 0.02148261 0.0219093 0.02234609 0.02279327 0.02325112 0.02371993 0.02420002 0.02469169 0.02519528 0.02571111 0.02623954 0.02678092 0.02733562 0.02790403 0.02848653 0.02908353 0.02969546 0.03032274 0.03096582 0.03162517 0.03230127 0.0329946 0.03370569 0.03443506 0.03518325 0.03595083 0.03673839 0.03754654 0.03837588] 说明 我们使用lomax.rvs()函数创建了随机变量，并使用具有随机值的numpy数组使用lomax.pdf()函数创建了概率分布。 程序3：图形化表示Lomax概率分布的程序。 代码 输出 Distribution : [0. 0.04081633 0.08163265 0.12244898 0.16326531 0.20408163 0.24489796 0.28571429 0.32653061 0.36734694 0.40816327 0.44897959 0.48979592 0.53061224 0.57142857 0.6122449 0.65306122 0.69387755 0.73469388 0.7755102 0.81632653 0.85714286 0.89795918 0.93877551 0.97959184 1.02040816 1.06122449 1.10204082 1.14285714 1.18367347 1.2244898 1.26530612 1.30612245 1.34693878 1.3877551 1.42857143 1.46938776 1.51020408 1.55102041 1.59183673 1.63265306 1.67346939 1.71428571 1.75510204 1.79591837 1.83673469 1.87755102 1.91836735 1.95918367 2. ]  说明 我们使用numpy数组打印了分布，然后使用matplotlib打印了使用概率密度函数的Lomax分布的图形。 程序4：图形化表示Lomax概率分布函数中变化的定位参数的程序。 代码 输出 [  说明 我们创建了一个线性、等间隔的numpy数组，然后使用概率密度函数绘制了两个不同Lomax分布的图形。 |
通常，当我们使用 print 语句打印一个字符串时，我们会使用另一个 print 语句在新的一行中打印另一个字符串。当我们编写一个 print 语句后，在其执行后，光标会自动移到新的一行。为什么会这样呢？我们不能...
阅读 4 分钟
os.getenv() 是一个 Python 函数，用于检索环境变量的值。环境变量是存储在操作系统环境中的键值对，操作系统环境是影响正在运行的进程行为的变量集合。
阅读 3 分钟
在本教程中，我们使用了 Python 中不同的数字数据类型，我们将学习如何将浮点值转换为整数值。让我们来看看实现相同目标的方法——使用 trunc() 使用 floor() 使用 ceil() 使用 int() 所以，让我们从第一个方法开始...
阅读 4 分钟
NumPy是Python中一个强大的库，它提供了一个用于操作大型多维数组和统计矩阵的指南，以及一组对这些数组进行操作的数学函数。一个方便的功能是在操作时可用...
阅读 4 分钟
在数据分析和决策中，统计学至关重要，它提供对不确定性和可变性复杂世界的洞察。从预测股票市场趋势到理解遗传特征，统计分布是建模和分析的基石。其中一个在...
阅读9分钟
序列化是将内存中的信息项转换为可保存或传输，然后重建为原始对象的布局。在 Python 中，序列化允许您将复杂的记录系统（例如列表、字典和自定义对象）存储到文档或传输...
阅读 3 分钟
？要检查给定数字是否为完全平方数，有几种方法可以使用 Python 中的各种内置函数和各种运算符。一些主要方法如下：方法 1：使用 math 模块中的 sqrt() 函数，您可以使用 sqrt()...
阅读 3 分钟
？YouTube是互联网上最受欢迎的视频分享平台之一。它拥有数百万个涵盖各种主题的视频。如果你对某个特定主题感兴趣，很可能有一个YouTube播放列表涵盖该主题。播放列表是...
11 分钟阅读
Python 的 Matplotlib 模块用于数据可视化。一组称为 pyplot 的方法，它是 matplotlib 的一个子模块，有助于创建各种图表。使用折线图在不同的轴上显示两组数据 X 和 Y 之间的关系。在这里，我们将研究...
阅读 6 分钟
在本教程中，我们将学习如何从字符串中删除单引号。有时，我们必须删除所有部分或仅删除字符串周围的部分。我们也可以删除单引号和双引号。我们将使用各种方法来删除引号；你可以...
阅读 2 分钟
我们请求您订阅我们的新闻通讯以获取最新更新。
我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
Python
Java
JavaScript
SQL
C
C++
HTML
CSS
React
Node.js
Spring Boot
C#
PHP
MySQL
MongoDB
AI
ML
DSA
DBMS
OS
Aptitude
Reasoning