Python 中的 Box-Cox 变换

在我们的环境中，数据是随机分布的，其中一些数据指的是数据集曲线的峰值，而另一些数据点则指的是曲线的尾部。对于任何数据集，我们可以通过其方差和均值来计算分布，并且可以看到数据距离均值的分布程度。

通常，我们可以将数据的分布分为两种方式

1. 正态分布
2. 非正态分布或幂律分布

正态分布

在这种分布类型中，数据沿均值的分布非常一致。在这里，我们在均值处获得曲线的峰值，并且数据沿均值对称分布。

我们可以轻松地对正态分布的数据实现分析技术。

幂律分布

在这种分布类型中，对于一些小型数据集，我们会得到曲线的峰值，然后对于大量数据集，我们会得到一条长尾曲线。

但是，在实际环境中，数据的性质并非总是正态分布的。因此，借助 box-cox 变换，我们可以使用一些数学公式将幂律分布的数据转换为正态分布的数据。

变换的数学分析是，我们将找到一个值，使得非正态分布的变换尽可能接近正态分布的数据集。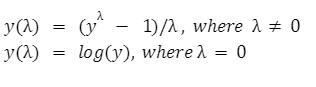

要实现 box-cox 变换，我们将使用 scipy 库，函数将是 scipy.stats.boxcox() 函数。

语法

InputArray

这是我们想将其转换为正态分布数据集的数据集。

Lamda

如果 lambda 为 none，我们将找出使对数函数值最大化的 lambda 值；如果 lambda 不是 none，则在 lambda 值上执行变换。

Alpha 版

这是一个可选参数，取值在 0.0 到 1.0 之间的浮点数。如果 lambda 为 none，则将其考虑在内；如果 lambda 不是 none，则忽略它。

Optimizer

这是一个可选的、可调用的参数，在需要时会被调用。当 lambda 值为 none 时，此优化器用于查找最小化对数函数值的 lambda 值。

示例

在此示例中，我们将采用非正态分布的数据集，然后将其转换为正态分布的数据集。

输出

说明

在上面的代码中，我们首先导入了文件中所需的模块，如 numpy、scipy、matplotlib 和 seaborn 来绘制曲线。现在，借助 numpy 的 random 函数，我们创建了 1200 个数据点的随机数据集。现在我们使用 boxcox() 函数，它将数据集作为参数，并返回变换后的数据集和 lambda 值。

现在，使用 histplot() 函数，我们绘制了原始数据集的曲线和变换后的数据集。histplot() 函数将数据集作为参数，并且还有许多其他属性，如 color、linewidth 等，它们定义了曲线的规格。现在，使用 show() 函数，我们显示了变换前和 boxcox 变换后的曲线。

对于上述随机数据集，我们得到的 lambda 值为 0.2872，接近于 0.28。

因此，在数据集中，新值将根据此公式计算：

New Value = (Old Value^0.2872 -1)/0.2872