Python 中的梯度下降优化器

2025年3月17日 | 阅读 8 分钟

梯度下降使用迭代算法来找到模型的最佳参数。其主要目标是通过找到该函数的参数值来最小化给定的函数。这些被称为最优参数。我们可以使用梯度下降来处理任何维度的函数，例如一维、二维或三维。在本教程中，我们将重点关注使用梯度下降算法确定众所周知的线性回归方程的理想参数。

我们将在Python中应用这一点。对于二维情况，我们将使用梯度下降来找到抛物线函数的全局最小值。
在深入研究算法实现之前，让我们确保我们拥有算法运行所需的参数。
我们首先需要一个需要最小化的成本函数，允许的迭代次数，算法在每次迭代中在接近最小值时选择步长的学习率，用于在每次迭代中更新参数的偏导数（用于偏差和权重），以及一个预测函数。
这些是实现梯度下降算法的要求。

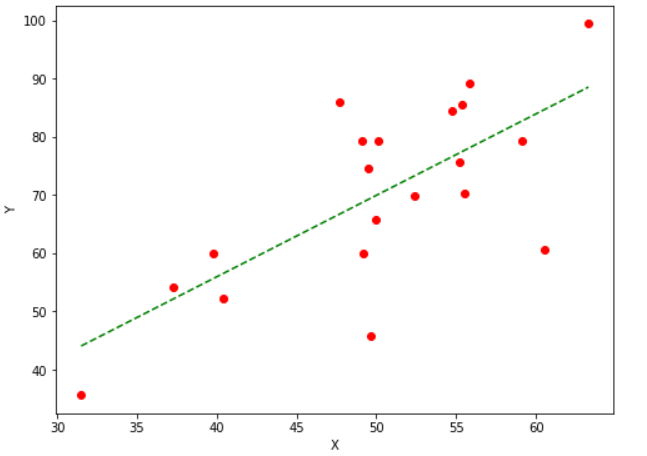
现在我们知道了算法所需的参数。为了完全理解梯度下降的工作原理，让我们将这些参数与算法进行映射，并手动处理一个示例。让我们以抛物线方程 y = 4x² 为例。通过将这些值代入函数，可以看到当 x = 0 时，即 x = 0, y = 0 时，该抛物线函数最低。因此，我们的抛物线函数 y = 4x² 的局部最小值在 x = 0 处。现在让我们看看梯度下降优化器的算法以及如何使用它来找到我们抛物线函数的局部最小值。

梯度下降算法

该算法在一个方向上工作，该方向基于当前位置处函数梯度负值的比例（沿梯度相反方向前进），以找到任何函数的局部最小值。梯度上升是一种通过以与函数梯度正值成比例的步长（沿梯度方向移动）来达到函数局部最大值的方法。

重复此块，直到收敛到所需值。

步骤 1：我们首先需要初始化所有重要参数。然后，我们必须为我们的抛物线函数 y = 4x² 推导出梯度函数。这是一个基本推导。4x² 的导数是 2x，因此导数将是 dy/dx = 8x。

x₀ = 4 (x 的随机值)

learning_rate = 0.02（这将决定算法为达到局部最小值而采取的步长）

gradient = Python中的梯度下降优化器 (梯度函数的计算)

步骤 2：例如，我们将执行三次梯度下降函数迭代。

对于每次迭代，我们必须根据前一次迭代的梯度下降值更新 x 的值。

第一次迭代

x₁ = x₀ - (learning_rate * gradient_equation)

x₁ = 4 - (0.02 * (8 * 4))

x₁= 4 - 0.64

x₁= 3.36

第二次迭代

x₂ = x₁ - (learning_rate * gradient_equation)

x₂ = 3.36 - (0.02 * (8 * 3.36))

x₂ = 3.36 - 0.54

x₂ = 2.82

第三次迭代

x₃ = x₂ - (learning_rate * gradient)

x₃ = 2.82 - (0.02 * (8 * 2.82))

x₃ = 2.82 - 0.45

x₃ = 2.37

从这三次梯度下降迭代中，我们可以看到 x 在每一步都在下降，并且通过继续进行梯度下降算法的更多迭代，它将逐渐收敛到 0，这是所需的值。下一个问题是算法需要多少次迭代才能收敛到给定函数的局部最小值？

我们可以设置一个阈值。这是两个 x 值之间的差，即当前值和前一个值。当这个差值小于阈值时，函数将停止迭代。我们将梯度下降应用于机器学习和深度学习模型的成本函数。其目的是最小化该成本函数。现在我们知道了梯度下降的幕后工作原理。让我们来看看它在 Python 中的实现。如前所述，我们将最小化线性回归模型的成本函数并找到最佳拟合线。在这种情况下，我们的参数将是 w 和 b。

预测函数

线性回归算法中的成本函数是直线的方程，即方程 Python中的梯度下降优化器

因此，预测函数将是 Python中的梯度下降优化器

这里，x 用于自变量

y 用于因变量

w 用于与自变量相关的权重

e 用于误差

成本函数

大多数机器学习模型都会进行某种预测或分类。在两种情况下，模型都会给出一些输出值。我们将这些预测值与我们拥有的观测值进行比较。模型中的损失定义为这两个值之间的差异，即预测值和观测值。对于线性回归，我们使用均方误差公式来计算损失。均方误差是通过找到观测值和预测值之间平方差的平均值来计算的。成本函数的方程如下所示。

这里，n 是样本数量。Y 是预测值，y 是观测值。

偏导数（梯度）

现在我们将计算成本函数相对于权重和误差项的偏导数。结果是

参数更新

参数将使用我们之前使用的公式进行更新。通过将学习率与其梯度相乘的结果减去参数。

在 Python 中实现梯度下降

为了实现上述算法，我们将定义两个函数。一个将使用上述成本函数返回成本值。该函数将以因变量的观测值和预测值作为参数。第二个函数将是实现梯度下降算法的函数。该函数将以自变量和因变量作为输入参数，并返回线性回归方程的权重和误差参数的最优值。

因此，它将为我们的数据提供最佳拟合线。我们可以调整梯度下降函数的参数，如迭代次数、学习率和停止阈值，使其更有效。为了实现这些函数，我们将创建自己的数据。我们已经取了一些近似线性相关的随机值。

使用梯度下降函数，我们将找到线性回归模型方程的最优参数，以找到此数据的最佳拟合线。迭代次数指定函数更新权重和误差值的次数；停止阈值是任何两个连续迭代中成本或损失值的变化的阈值或最小值。

代码

# Python program to show how to implement Gradient Descent 

# Importing the required libraries
import numpy as np
import matplotlib.pyplot as plt

# Creating a function to calculate the mean squared error for the observed and the predicted values
def mean_sq_error(y_true, y_pred):
     
    # Calculating the cost function for the model
    cost = np.sum((y_true - y_pred) ** 2) / len(y_true)
    return cost
 
# Implimenting the Gradient Descent Function
# We will pass the numbers of iterations, learning rate, and the stopping threshold value
# We can tune these parameters as we want
def gradient_descent(x, y, iter = 1000, learning_rate = 0.0001, threshold = 1e-6):
     
    # Initializing the values of weight, error, learning rate, and the number of iterations for the function
    curr_weight = 0.1
    curr_error = 0.01
    iter = iter
    learning_rate = learning_rate
    n = float(len(x))
     
    cost = []
    weight = []
    prev_cost = None
     
    # Estimating the optimal parameters for the regression model equation
    for i in range(iter):
         
        # Calculating the predicted values
        y_pred = (curr_weight * x) + curr_error
         
        # Calculating the value of cost with current parameters
        curr_cost = mean_sq_error(y, y_pred)
 
        # If the change in the previous cost and the current cost values is less than or equal to the stopping threshold value, then the gradient descent iterations will be stopped.
        if prev_cost and abs(prev_cost - curr_cost) <= threshold:
            break
         
        prev_cost = curr_cost
 
        cost.append(curr_cost)
        weight.append(curr_weight)
         
        # Calculating the value of gradients for the linear regression equation
        derivative_weight = -(2 / n) * sum(x * (y - y_pred))
        derivative_error = -(2 / n) * sum(y - y_pred)
         
        # Updating the values of weights and errors based on the derivatives
        curr_weight = curr_weight - (learning_rate * derivative_weight)
        curr_error = curr_error - (learning_rate * derivative_error)
                 
        # Printing the values of parameters for each 500th iteration
        print(f"At iteration {i + 1}: The value of cost: {curr_cost}, weight: {curr_weight}, and the error is: {curr_error}")
     
     
    # Plotting the cost and weight values for each iterating to visualize the convergence of the parameters
    plt.figure(figsize = (8, 6))
    plt.plot(weight, cost)
    plt.scatter(weight, cost, marker = 'o', color = 'red')
    plt.title("Cost vs Weight For the Linear Regression Model")
    plt.ylabel("Cost")
    plt.xlabel("Weight")
    plt.show()
     
    return curr_weight, curr_error
 
 
# Calling the function and passing the following values to the gradient descent function
     
# Data
X = np.array([31.502527, 52.426403, 60.53035803, 49.47563963, 55.81320787,
        50.14218841, 55.21179669, 37.29956669, 49.10504169, 55.55001444,
        40.41973014, 55.35163488, 49.1640495, 59.16847072, 54.72720806,
        49.95588857, 47.68719623, 63.29732685, 49.61864377, 39.81681754])
Y = np.array([35.70700585, 69.77759598, 60.5623823 , 74.54663223, 89.23092513,
        79.21151827, 75.64197305, 54.17148932, 79.3312423, 70.30087989,
        52.16567715, 85.47884676, 60.00892325, 79.39287043, 84.43619216,
        65.72360244, 85.89250373, 99.37989686, 45.84715332, 59.87721319])

# Estimating the values of weight and error using the gradient descent algorithm
est_weight, est_error = gradient_descent(X, Y, iter = 2000)
print(f"The estimated value of weight is: {est_weight} and the estimated error is: {est_error}")

# Finding the predicted values using the model with estimated weight and error
Y_pred = est_weight * X + est_error

# Plotting the linear regression line for our data
plt.figure(figsize = (8, 6))
plt.scatter(X, Y, marker = 'o', color = 'red')
plt.plot([min(X), max(X)], [min(Y_pred), max(Y_pred)], color = 'green',markerfacecolor = 'red',
          markersize = 10,linestyle = 'dashed')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

输出

At iteration 1: The value of cost: 4490.368112564136, weight: 0.7732901495653765, and the error is: 0.023058581526390003
At iteration 2: The value of cost: 1131.6506097576817, weight: 1.0973277566276178, and the error is: 0.02933947690034616
At iteration 3: The value of cost: 353.6864536509919, weight: 1.2532789421408856, and the error is: 0.0323584432495475
At iteration 4: The value of cost: 173.49022435062597, weight: 1.3283343812503887, and the error is: 0.033807525620796475
At iteration 5: The value of cost: 131.75220717474858, weight: 1.3644567422091003, and the error is: 0.03450106252964878
At iteration 6: The value of cost: 122.08462343134752, weight: 1.3818415966647506, and the error is: 0.03483097452170135
At iteration 7: The value of cost: 119.84536542439749, weight: 1.3902085628198768, and the error is: 0.034985883049982396
At iteration 8: The value of cost: 119.32669605130852, weight: 1.394235447257572, and the error is: 0.03505656685253503
At iteration 9: The value of cost: 119.20655864249093, weight: 1.3961735600573946, and the error is: 0.03508671544159867
At iteration 10: The value of cost: 119.17873134396095, weight: 1.3971063998600626, and the error is: 0.03509735547518664
At iteration 11: The value of cost: 119.17228540809819, weight: 1.397555427176545, and the error is: 0.03509860655236391
At iteration 12: The value of cost: 119.170791938096, weight: 1.3977716077711553, and the error is: 0.0350953389803933
At iteration 13: The value of cost: 119.17044558479306, weight: 1.3978757251232417, and the error is: 0.03508989671506608
At iteration 14: The value of cost: 119.17036493281425, weight: 1.397925909268681, and the error is: 0.035083407843062374
At iteration 15: The value of cost: 119.17034582400478, weight: 1.3979501367245375, and the error is: 0.035076415283989484
At iteration 16: The value of cost: 119.1703409701581, weight: 1.3979618718813835, and the error is: 0.035069180331332335
At iteration 17: The value of cost: 119.17033941812645, weight: 1.3979675948100971, and the error is: 0.0350618287390411





The estimated value of weight is: 1.3979675948100971 and the estimated error is: 0.0350618287390411

下一主题如何在 Python 中向字符串添加字符

Python 中的梯度下降优化器

梯度下降算法

预测函数

成本函数

在 Python 中实现梯度下降

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

Python 问题

Python 中的梯度下降优化器

梯度下降算法

预测函数

成本函数

在 Python 中实现梯度下降

相关帖子

Python 程序生成随机字符串

pywhatkit 库简介

Python Paramiko 模块

使用 Python 进行职业愿望调查分析

Python 中的前缀转中缀转换

编写 Python 程序查找列表中第一个重复的元素

Python 中使用二分查找的第一次出现

在 Jupyter Notebook 中使用 Matplotlib

Python 中的 Log 函数

Python 中的二项分布

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器