在 Python 中实现线性回归

线性回归是一种统计技术，用于描述因变量与若干自变量之间的关系。本教程将讨论线性回归的基本概念及其在 Python 中的应用。

为了帮助理解线性回归的基本概念，我们从最简单的线性回归形式开始，即“简单线性回归”。

简单线性回归

简单线性回归 (SLR) 是一种使用一个特征来预测响应的方法。它假定两个变量是线性相关的。因此，我们试图找到一个线性方程，该方程能够尽可能精确地根据特征或独立派生变量 (x) 来预测响应值 (y)。

让我们考虑一个数据集，其中我们有多个特征 x 对应的响应 y。

为简化起见，我们定义

x 为 **特征向量**，即 x = [x₁, x₂, x₃, …., x_n]，

y 为 **响应向量**，即 y = [y₁, y₂, y₃ …., y_n]

对于 **n** 个观测值（以上面的例子为例，n = 10）。

上述数据集的散点图如下所示：-

下一步是确定最适合此散点图的直线，以便我们可以预测特征的任何新值的响应（即，x 的值不在数据集中）。

这条线称为回归线。

回归线的方程可以表示如下：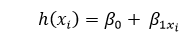

此处，

• h(x_i ) 表示第 i 个观测值的 **预测响应值**。
• ?₀ 和 ?_1xi ) 是回归系数，分别表示回归线的 **y 截距** 和 **斜率**。

为了构建我们的模型，我们需要“学习”或估计回归系数 ?₀ 和 ?₁ 的值。在我们确定了这些系数之后，我们就可以利用这个模型来进行响应预测了！

在本教程中，我们将采用 **最小二乘法** 的概念。

让我们考虑

y_i = ?₀+ ?_1xi + ?_i=h(x_i )+ ?_i ? ?_i= y_i- h(x_i )

这里，?_i 是第 i 个观测值的 **残差误差**。

因此，我们的目标是最小化总残差误差。

我们将成本函数或平方误差 **J** 定义为

我们的任务是找到 ?₀ 和 ?₁ 的值，使得 J(?₀,?₁) 最小。

在不深入数学细节的情况下，我们给出以下结果：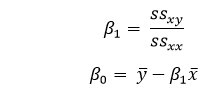

其中，ss_xy 是“y”和“x”的偏差之和。

而 ss_xx 是“x”的平方偏差之和。

代码

输出

Estimated coefficients are :
b_0 = -0.4606060606060609 		
b_1 = 1.1696969696969697

多元线性回归

多元线性回归试图解释多个要素之间的关系，然后通过将线性方程应用于数据来响应。显然，这不过是线性回归的扩展。

设想一个数据集，其中包含一个或多个特征（或自变量）以及一个响应（或因变量）。

数据集还包含另外 n 行/观测值。

我们定义

**X** (特征矩阵) = 这是一个大小为 **“n * p”** 的矩阵，其中“x_ij”表示第 i 个观测值的第 j 个属性的值。

因此，

并且，

**y** (响应向量) = 这是一个大小为 **n** 的向量，其中表示第 i 个观测值的响应值。

对于“p”个特征的回归线表示为：

其中 h(x_i) 是第 i 个观测点的预测响应值，而 ?₀,?₁,?₂,....,?_p 是回归系数。

我们也可以写成：

其中，?_i 表示第 i 个观测点的残差误差。

我们也可以通过将“X”的属性矩阵表示为来进一步推广我们的线性模型：

因此，线性模型可以用矩阵形式表示如下：

y=X?+?

其中，

我们现在使用一种称为最小二乘法的算法来确定 b 的估计值，即 b'。如前所述，这种最小二乘法用于在总残差误差最小的情况下找到 b'。

我们将给出以下结果：

其中 ' 是矩阵的转置，-1 是矩阵的逆。

借助最小二乘估计 b'，多元线性回归模型现在由以下公式计算：

其中 y' 是估计的响应向量。

代码

输出

Regression Coefficients are:  [-8.95714048e-02  6.73132853e-02  5.04649248e-02  2.18579583e+00
 -1.72053975e+01  3.63606995e+00  2.05579939e-03 -1.36602886e+00
  2.89576718e-01 -1.22700072e-02 -8.34881849e-01  9.40360790e-03
 -5.04008320e-01]
Variance score is: 0.7209056672661751

在上面的示例中，我们使用方差得分来计算准确性得分。

我们定义

explained_variance_score = 1 - Var{y - y'}/Var{y}

其中 y' 是估计的输出目标，y 是对应的（正确的）目标输出，Var 是方差，它是标准差的平方。

最佳得分是 1.0。分数越低越差。

假设

以下是线性回归模型在用于数据集时所基于的主要假设：

• **线性关系**：特征变量和响应变量之间的关系必须是线性的。线性假设是通过散点图来检验的。如我们所见，第一个图表示线性相关的变量，而第三个和第二个图中的变量可能是非线性的。因此，第一个图可以使用线性回归进行更准确的预测。
  
• **多重共线性少或无**：假设数据中存在最少或不存在多重共线性。当特征（或自变量）彼此不独立时，就会发生多重共线性。
• **自相关少或无**：另一个理论是数据中不存在或很少存在自相关。自相关是指残差误差不相互独立。
• **同方差性**：同方差性指的是误差是一个因子（即，自变量和因变量之间关系中的“噪声”或随机扰动）对于所有自变量都保持不变的情况。图 1 是同方差的，而图 2 显示了异方差性。

在本教程的最后，我们将讨论线性回归的一些应用。

应用

以下是基于线性回归的应用领域：

• **趋势线**：说明数据量随时间的变化（例如，GDP 或油价）。它们通常具有线性关系。因此，可以使用线性回归来预测未来值。然而，当其他可能的变化会改变数据时，该方法无法满足科学可靠性的要求。
• **经济学**：线性回归是经济学中的主要工具。它可以用来预测消费支出、固定投资支出、库存投资、国家出口购买、进口支出、持有流动资产的需求、劳动力需求和供给。
• **金融学**：资本资产定价模型利用线性回归来研究和量化投资的风险因素。
• **生物学**：线性回归是解释生物系统中变量之间因果关系的一种方法。