使用 Python 进行有限自动机算法模式搜索

在接下来的教程中，我们将学习用于模式搜索的有限自动机算法，并讨论在 Python 编程语言中实现该算法的方法。

但在我们开始之前，让我们先了解一下什么是有限自动机。

有限自动机简介

有限自动机是用于识别输入序列中模式的抽象机器，构成了计算机科学中理解正则语言的基础。它们主要由五个主要元素或元组组成，包括：

1. 输入
2. 输出
3. 自动机状态
4. 状态关系
5. 输出关系

自动机由不同的状态和规则组成，使其能够根据输入符号从一个状态转移到另一个状态。如果机器在处理完输入后最终处于接受状态，则输入被接受；否则，被拒绝。有限自动机分为确定性（DFA）和非确定性（NFA），两者都可以识别同一组正则语言。它们通常用于文本处理、网络协议和编译器中。

有限自动机的主要特点

有限自动机的主要特点如下：

1. 输入： 提供给机器进行处理的字符或符号集。
2. 输出： 处理输入模式后，机器要么接受要么拒绝它。
3. 自动机状态： 定义机器的配置和条件。
4. 状态关系： 显示状态之间的转换。
5. 输出关系： 根据最终状态做出输出决定。

理解有限自动机的形式化定义

有限自动机是一种机器，可以定义为一个元组：

{Q, Σ, q, F, δ}

其中

1. Q：状态的有限集合
2. Σ：输入符号的集合
3. q：初始状态
4. F：最终状态的集合
5. δ：转移函数

理解有限自动机的类型

有限自动机主要有两种类型：

1. 确定性有限自动机（DFA）
2. 非确定性有限自动机（NFA）

让我们在下一节中理解这两种类型。

1. 确定性有限自动机 (DFA)

确定性有限自动机，简称为 DFA，表示为 {Q, Σ, q, F, δ}。在 DFA 中，对于每个输入符号，机器只转移到一个状态。DFA 不允许任何空转换，这意味着每个状态对于每个输入符号都必须有明确的转换。

DFA 主要由五个元组组成：

{Q, Σ, q, F, δ}

其中

1. Q：所有状态的集合
2. Σ：输入符号的集合
3. q：初始状态
4. F：最终状态的集合
5. δ：转移函数，定义为 δ: Q X Σ --> Q

让我们看一个构建 DFA 的例子。

示例： 构建一个确定性有限自动机（DFA），其中 Σ = {a, b}，接受所有以 'a' 结尾的字符串。

解决方案

• Σ = {a, b}
• Q = {q₀, q₁}
• F = {q₁}

图 1： 对于 Σ = {a, b} 的 DFA 状态转移图

上述自动机的状态转移表如下所示：

在这个例子中，如果字符串以 'a' 结尾，机器将达到状态 q₁，这是一个接受状态。

2. 非确定性有限自动机 (NFA)

非确定性有限自动机，简称为 NFA，与 DFA 类似。然而，它具有以下特点：

1. 对于相同的输入，可能转换到多个状态。
2. 我们可以在 NFA 中使用空（ϵ）移动，即机器可以在不消耗任何输入的情况下改变状态。

让我们看一个构建 NFA 的例子。

示例： 构建一个非确定性有限自动机（NFA），其中 Σ = {a, b}，接受所有以 'a' 结尾的字符串。

解决方案

• Σ = {a, b}
• Q = {q₀, q₁}
• F = {q₁}

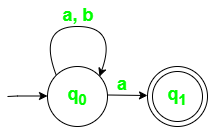图 2： 对于 Σ = {a, b} 的 NFA 状态转移图

上述自动机的状态转移表如下所示：

在 NFA 中，如果任何一个转换导致接受状态，那么该字符串就被接受。

现在我们已经对有限自动机有了基本的了解，是时候讨论使用有限自动机进行模式匹配及其在 Python 中的实现了。

模式搜索简介

模式搜索，也称为模式匹配，是计算机科学中的一个基本问题，在文本处理和生物信息学等领域有多种应用。解决这个问题的一种高效方法是使用基于有限自动机的模式搜索算法。在下一节中，我们将探讨该算法的工作原理及其在 Python 中的实现。

理解问题陈述：基于有限自动机的模式搜索算法

我们给定一个输入字符串 str[0….. m - 1] 和一个模式字符串 ptn[0…. n - 1]。我们需要编写一个函数来从输入字符串中搜索模式。该函数将接受两个参数——分别为 char ptn[ ] 和 char str[ ]。然后，该函数将返回模式字符串 ptn[ ] 在输入字符串 str[ ] 中出现的次数。我们可以假设输入字符串的长度大于模式字符串的长度（m > n）。

让我们看一些例子以便更好地理解问题。

示例 1

示例 2

Input:
str [ ] = "AABBAADAABBAACCAA"  
ptn [ ] = "AABBAA"  
Output:
The Pattern "AABBAA" is found at index 0 and 7.

图 3： 一个说明模式匹配的例子

理解基于有限自动机的模式搜索算法的方法

以下是我们将遵循的步骤，以实现基于有限自动机的模式搜索算法：

步骤 1： 首先，我们将构建一个接受输入字符串的有限自动机，以便在输入字符串中搜索模式。

步骤 2： 之后，我们将仅分析输入字符串的每个字符一次，以搜索模式。

理解在输入字符串中搜索模式的算法

我们现在来看看我们将用于在给定输入字符串中搜索模式的算法。

步骤 1：构建转移函数 (TF) 表

步骤 1.1： 转移函数（TF）表将根据输入符号和字符显示 DFA 状态之间的转换。

步骤 1.2： 我们可以通过遍历所有可能的状态和符号来构建它，根据当前状态和输入符号确定下一个状态。

步骤 1.3： get Next State 函数根据当前状态和输入符号计算下一个状态。

步骤 2：在文本上遍历 DFA

步骤 2.1： 一旦我们构建了 TF 表，我们将在文本上遍历 DFA，以搜索和匹配输入文本中模式的出现。

步骤 2.2： 我们将从初始状态（状态 0）开始，DFA 根据文本中的字符转换到后续状态。

步骤 2.3： 如果当 DFA 到达最终状态（代表模式的结束）时找到匹配，则存储该出现的索引。

步骤 3：打印结果

步骤 3.1： 如果在遍历过程中找到匹配，我们将打印该出现的索引。

步骤 3.2： 如果没有找到匹配，我们将打印在输入文本中未找到该模式。

基于有限自动机的模式搜索算法的实现

模式匹配自动机非常高效，因为它们对每个文本字符只检查一次，每个文本字符耗时为常数时间。因此，我们可以说匹配字符串所需的时间是 O(n)，其中 n 是文本字符串的长度。然而，预处理时间（构建有限自动机所需的时间）可能会很长。

在我们开始构建有限自动机之前，让我们考虑以下针对模式 ABABACA 的有限自动机。

图 4： 模式 ABABACA 的有限自动机

模式 ABABACA 的表格表示如下

有限自动机中的状态数将为 M + 1，其中 M 是模式的长度。构建有限自动机的主要目标是根据当前状态为每个可能的字符获取后续状态。

给定一个字符 c 和一个状态 k，我们可以通过考虑字符串 'ptn[0 … k - 1]c' 来得到下一个状态，这基本上是模式字符 ptn[0], ptn[1], … ptn[k - 1] 和字符 c 的连接。主要目标是返回给定模式的最长前缀的长度，使得该前缀也是字符串 'ptn[0 … k - 1]c' 的后缀。该长度值提供了下一个状态。

假设我们需要从上图中的当前状态 5 和字符 'B' 找到下一个状态。我们必须考虑字符串 'ptn[0 … 4]B'，即 'ABABAB'。该模式的最长前缀，且该前缀是 'ABABAB' 的后缀，其长度为 4 ('ABAB')。因此，对于字符 'B'，下一个状态（从状态 5）是 4。

在下面的程序中，我们将定义一个函数来允许我们构建有限自动机。该函数的时间复杂度将为 O(M³ * N)，其中 M 是模式字符串的长度，N 是字母表的大小（给定模式和文本中所有可能字符的总数）。该实现试图从可能是 'ptn[0 … k - 1]c' 后缀的最长可能序列开始，获取所有可能的前缀。有多种实现可以用来在 O(M * N) 的时间内构建有限自动机。

有限自动机的图形表示

模式 'ptn' 的有限自动机 (FA)

在上图中：

1. 每个框代表有限自动机中的一个状态。
2. 初始状态由状态 0 表示。
3. 根据输入字符，状态之间存在转换（由箭头表示）。
4. 转换标有相应的输入字符。
5. 状态 3 是最终状态，表示匹配了整个模式 'ptn'。

转移函数 (TF) 表

在下表中：

1. 每行代表一个状态，每列代表一个输入字符。
2. 表中的值根据当前状态和输入字符显示要转换到的下一个状态。
3. 例如，TF[1]['a'] = 1 表示当当前状态等于 1 且输入字符为 'a' 时，下一个状态将是 1。
4. 最终状态由除了对角线元素被设置为最终状态外，所有元素都为零的行表示。

这些图形表示有助于可视化用于模式搜索的有限自动机算法中涉及的转换和状态，有助于理解其工作原理和效率。

使用有限自动机算法搜索模式的 Python 程序

我们现在来看下面的 Python 程序，以理解基于有限自动机的模式搜索算法的实现。

示例

输出

# Output 1
Enter the Text: HELLO STUDENTS WELCOME TO PYTHON TUTORIALS
Enter the Pattern to be searched: TS
Pattern found at index: 12
# Output 2
Enter the Text: AABBAADAABBAACCAA
Enter the Pattern to be searched: AABBAA
Pattern found at index: 0
Pattern found at index: 7
# Output 3
Enter the Text: ABABABAC
Enter the Pattern to be searched: ABA
Pattern found at index: 0
Pattern found at index: 2
Pattern found at index: 4
# Output 4
Enter the Text: ABCADBCAADBCDAABCAADB
Enter the Pattern to be searched: AAAB
Pattern not found!

说明

在上面的代码片段中，我们初始化了一个常量。然后我们定义了一个函数，根据当前状态和输入字符返回下一个状态。接着，我们定义了另一个函数来计算给定模式的转移函数。然后我们定义了在输入字符串中搜索给定模式的函数。这个函数接受两个参数——ptn 和 txt。在这个函数内部，我们计算了模式和字符串的长度，将初始状态设置为 0，通过调用 compute_transition_function() 计算转移函数，并最初将模式找到标志设置为 False。然后我们遍历给定的输入文本并开始匹配模式。如果找到模式，我们将打印匹配的索引；否则打印“未找到模式”。对于主函数，我们从用户那里收集输入字符串和模式，并对给定的字符串和模式调用 search() 函数。

基于有限自动机的模式搜索算法的时间和空间复杂度

时间复杂度

1. 预处理（计算转移函数）

• compute_transition_function() 函数允许我们为给定的有限自动机构建转移函数 (TF) 表。
• 该函数遍历从 0 到 M（其中 M 是模式的长度）的每个状态，并且对于每个状态，它遍历字母表中的每个字符（NUMBER_OF_CHARACTERS，通常是 256）。
• 在嵌套循环内，该函数调用 get_next_state() 函数，在最坏情况下需要 O(M) 的时间。
• 因此，整个预处理步骤的时间复杂度为 O(M² * NUMBER_OF_CHARACTERS)，其中 M 是模式的长度，NUMBER_OF_CHARACTERS 是字母表的大小。

2. 模式搜索

• 为了在给定的输入字符串中搜索模式，我们定义了一个名为 search() 的函数，它遍历文本中的每个字符。
• 在循环内部，此函数借助当前状态和给定文本中当前位置的字符，在转移表 (TF) 中执行常数时间查找。
• 因此，我们可以说整个模式搜索步骤需要 O(N) 的时间，其中 N 是文本的长度。

最后，我们可以得出结论，基于有限自动机的模式搜索算法的总体时间复杂度主要由预处理步骤决定，得到 O(M² * NUMBER_OF_CHARACTERS)，其中 M 是模式的长度，NUMBER_OF_CHARACTERS 是字母表的大小。如果字母表的大小被认为是常数，则该算法的时间复杂度简化为 O(M²)。

空间复杂度

基于有限自动机的模式搜索算法的空间复杂度主要取决于在算法预处理阶段设计的转移函数 (TF) 表的大小。

让我们分析一下该算法空间复杂度的不同组成部分：

1. 转移函数 (TF) 表

• 转移函数 (TF) 表是一个大小为 (M + 1) * NUMBER_OF_CHARACTERS 的二维数组，其中 M 是模式的长度，NUMBER_OF_CHARACTERS 是字符集的大小（对于 ASCII 字符通常为 256）。
• 转移函数 (TF) 表中的每个条目都根据输入字符显示从一个状态到另一个状态的转换。
• 因此，转移函数 (TF) 表的空间复杂度为 O((M + 1) * NUMBER_OF_CHARACTERS)，其中 M 是模式的长度。

2. 其他变量

• 除了 TF 表之外，该算法还利用其他变量来存储文本、模式和中间状态的信息。
• 然而，与 TF 表相比，这些变量对整体空间复杂度的影响可以忽略不计。

根据以上陈述，我们可以得出结论，空间复杂度中的主导因素是 TF 表。因此，基于有限自动机的模式搜索算法的整体空间复杂度为 O((M + 1) * NUMBER_OF_CHARACTERS)，其中 M 是模式的长度，NUMBER_OF_CHARACTERS 是字母表的大小。

结论

最后，我们可以得出结论，基于有限自动机的模式搜索算法通过采用确定性有限自动机（DFA）的思想，为模式搜索问题提供了高效的解决方案。该算法的实现包括构建转移函数（TF）表和在文本上遍历 DFA，使其成为各种模式搜索活动的多功能且有效的方法。

此外，理解该算法为高效模式搜索方法及其在现实世界场景中的实际应用提供了重要的见解。