NCERT 10年级数学第一章：实数

练习1.1

1. 使用欧几里得除法算法求以下数的 HCF（最大公约数）：

1. 135 和 225
2. 196 和 38220
3. 867 和 255

解决方案

I. 因为 225 > 135，我们可以将欧几里得除法算法 a=bq + r; 0≤ r < b 应用于 a=225 和 b=135。

225 = 135 × 1 + 90，其中 r=90

因为 r≠0，我们将对 b = 135 和 r = 90 重新应用该算法。

135 = 90×1 + 45，其中 r1=45

因为 r1≠0，我们将对 b1=90 和 r1=45 重新应用该算法。

90 = 45×2 + 0，其中 r2=0

我们得到 r2=0。

因此，135 和 225 的 HCF 是 45。

II. 因为 38220 > 196，我们可以将欧几里得除法算法 a=bq + r; 0≤ r < b 应用于 a=38220 和 b=196。

38220 = 196×195 + 0

我们得到 r=0。

因此，196 和 38220 的 HCF 是 196。

III. 因为 867 > 255，我们可以将欧几里得除法算法 a=bq + r; 0≤ r < b 应用于 a=867 和 b=255。

867 = 255 × 3 + 102，其中 r=102

因为 r≠0，我们将对 b = 255 和 r = 102 重新应用该算法。

255 = 102×2 + 51，其中 r1=51

因为 r1≠0，我们将对 b1=102 和 r1=51 重新应用该算法。

102 = 51×2 + 0，其中 r2=0

我们得到 r2=0。

因此，867 和 255 的 HCF 是 51。

2. 证明任何正奇数都可以表示为 6q + 1、6q + 3 或 6q + 5 的形式，其中 q 是某个整数。

解决方案

设 a 为一个正奇数，使得

a=6q + r; 0≤ r< 6 （根据欧几里得除法引理）

其中 q 是商，r 是余数。

因为 0≤ r< 6，我们可以用 0、1、2、3、4 或 5 来代替 r。在每种情况下，我们得到以下结果：

如前所述，a 是一个正奇数。因此，r 不能等于 2 或 4，因为

a=6q、a=6q+2 和 a=6q+4 将 a 表示为偶数，这是错误的。

因此，一个正奇数只能是 6q+1、6q+3 或 6q+5 的形式。

3. 一个 616 人的军队特遣队要在阅兵式上跟随 32 人的军乐队行进。两组队伍要以相同数量的纵队行进。他们可以行进的最大纵队数是多少？

解决方案

从问题中可以清楚地看出，我们需要找到最大纵队数，即 616 和 32 的 HCF。

因为 616 > 32，我们可以将欧几里得除法算法 a=bq + r; 0≤ r < b 应用于 a=867 和 b=32。

616 = 32 × 19 + 8，其中 r=8

因为 r≠0，我们将对 b = 32 和 r = 8 重新应用该算法。

32 = 8×4 + 0，其中 r1=0

我们得到 r1=0。

因此，616 和 32 的 HCF 是 8。

因此，616 人的军队特遣队在 32 人的军乐队后面行进的最大纵队数是 8。

4. 使用欧几里得除法引理证明任何正整数的平方都具有 3m 或 3m + 1 的形式，其中 m 是某个整数。

解决方案

设 a 为一个正整数。

将 b=3 应用欧几里得除法引理后，我们得到

a=3q + r; 0≤ r< 3

因此，a 可以具有以下形式：

a=3q, a=3q+1 或 a=3q+2

将每个方程两边平方，我们得到

a²=9q²

a²=3(3q²)

a²=3m; 其中 m=3q²

a²=9q²+1+6q

a²=3(3q² +2q) +1

a²=3m+1; 其中 m=3q² +2q

a²=9q² +4+12q

a²=3(3q²+4q+1) +1

a²=3m+1; 其中 m=3q²+4q+1

因此，任何正整数的平方总是具有 3m 或 3m+1 的形式。

5. 使用欧几里得除法引理证明任何正整数的立方都具有 9m、9m + 1 或 9m + 8 的形式。

解决方案

设 a 为正整数。

将 b=3 应用欧几里得除法引理后，我们得到

a=3q+r; 0≤ r< 3

因此，a 可以具有以下形式：

a=3q, a=3q+1 或 a=3q+2

将每个方程两边立方，我们得到

a³=27q³

a³=9(3q³)

a³=9m 其中 m=3q³

a³=27q³ + 1+ 27q³+ 9q

a³=9(3q³+3q² + q) +1

a³=9m+1 其中 m=3q³+3q² + q

a³=27q³+ 8+ 54q³+36q

a³=9(3q³+6q² + 4q) +8

a³=9m +8 其中 m=3q³+6q² + 4q

因此，任何正整数的立方总是具有 9m、9m+1 或 9m+8 的形式。

练习1.2

1. 将每个数表示为其质因数的乘积

1. 140
2. 156
3. 3825
4. 5005
5. 7429

I. 通过应用质因数分解，

II. 通过应用质因数分解，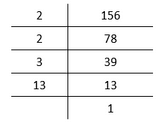

III. 通过应用质因数分解，

IV. 通过应用质因数分解，

V. 通过应用质因数分解，

2. 求以下整数对的 LCM（最小公倍数）和 HCF（最大公约数），并验证 LCM × HCF = 两个数的乘积。

1. 26 和 91
2. 510 和 92
3. 336 和 54

解决方案

I. 应用质因数分解求 LCM 和 HCF

26 = 2 × 13

91 = 7 × 13

因此，HCF(26, 91)=13，LCM(26, 91) = 2 × 7 × 13 = 182。

两个数的乘积 = 26 × 91 = 2366

LCM × HCF = 182 × 13 = 2366。

因此，已验证两个数的乘积等于 LCM × HCF。

II. 应用质因数分解求 LCM 和 HCF

510 = 2 × 3 × 5 × 17

92 = 2 × 2 × 23

因此，HCF(510, 92) = 2，LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460。

两个数的乘积 = 510 × 92 = 46920

LCM × HCF = 23460 × 2 = 46920。

因此，已验证两个数的乘积等于 LCM × HCF。

III. 应用质因数分解求 LCM 和 HCF

336 = 2 × 2 × 2 × 2 × 3 × 7

54 = 2 × 3 × 3 × 3

因此，HCF(336, 54) = 2 × 3 = 6，

LCM(336, 54) = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024。

两个数的乘积 = 336 × 54 = 18144

LCM × HCF = 3024 × 6 = 18144。

因此，已验证两个数的乘积等于 LCM × HCF。

3. 通过应用质因数分解方法求以下整数的 LCM 和 HCF。

1. 12、15 和 21
2. 17、23 和 29
3. 8、9 和 25

解决方案

I. 通过进行质因数分解，我们得到

12 = 2 × 2 × 3

15 = 3 × 5

21 = 3 × 7

HCF (12, 15, 21) = 3

LCM (12, 15, 21) = 2 × 2 × 3 × 5 × 7 = 420

II. 通过进行质因数分解，我们得到

17 = 17 × 1

23 = 23 × 1

29 = 29 × 1

HCF (17, 23, 29) = 1

LCM (17, 23, 29) = 17 × 23 × 29 = 11339

III. 通过进行质因数分解，我们得到

8 = 2 × 2 × 2

9 = 3 × 3 × 3

25 = 5 × 5

HCF (8, 9, 25) = 1

LCM (8, 9, 25) = 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800

4. 已知 HCF (306, 657) = 9，求 LCM (306, 657)。

解决方案

因为已知

两个给定数的乘积 = LCM × HCF

因此，

306 × 657 = LCM × 9

解上述方程，我们得到

LCM = 22338

因此，LCM (306, 657) = 22338

5. 检查 6ⁿ 对于任何自然数 n 是否可能以数字 0 结尾。

解决方案

如果 5 是 6 的质因数之一，则 6ⁿ 将以 0 结尾。

通过使用质因数分解，我们有

6 = 2 × 3

因为 5 不是 6 的质因数，所以 6ⁿ 永远不能以数字 0 结尾。

6. 解释为什么 7 × 11 × 13 + 13 和 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 是合数。

解决方案

设 7 × 11 × 13 + 13 = a 且 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = b。

a = 7 × 11 × 13 + 13

= 13 × (7 × 11 × 1 + 1)

= 13 × (77 + 1)

= 13 × 78

= 13 × 2 × 3 × 13 （78 的质因数分解）

因为 a 可以表示为素数乘积，所以它是一个合数。

b = 7 × 6 × 5 × 4 × 3 × 2 + 5

= 5 × (7 × 6 × 1 × 4 × 3 × 2 + 1)

=5 × (1008 + 1)

= 5 × 1009

因为 b 可以表示为素数乘积，所以它是一个合数。

因此，7 × 11 × 13 + 13 和 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 都是合数。

7. 体育场周围有一个圆形跑道。索尼雅绕场跑一圈需要 18 分钟，而拉维需要 12 分钟。假设他们都在同一点、同一时间出发，并朝同一方向前进。他们将在多少分钟后在起点再次相遇？

解决方案

索尼雅需要 18 分钟，而拉维需要 12 分钟。

为了找到他们再次在起点相遇时经过的时间（以分钟为单位），我们需要计算 18 和 12 的 LCM（每个人完成一圈所需的时间）。

通过质因数分解，

18 = 2 × 3 × 3

12 = 2 × 2 × 3

LCM = 2 × 2 × 3 × 3 = 36

因此，他们将需要 36 分钟才能在起点再次相遇。

练习1.3

1. 证明 √5 是无理数。

解决方案

我们假设 √5 是有理数。

因为 √5 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得

√5 = a/b

b√5 = a

两边平方

5b² = a² …… (I)

从方程可以推断出 a² 被 5 整除，这进一步意味着 a 也能被 5 整除。

因此，我们可以写成

a = 5c，其中 c 是整数。

如果我们把 a 的值代入 (I)，我们得到

5b² = 25c²

b² = 5c²

从方程可以推断出 b² 被 5 整除，这进一步意味着 b 也能被 5 整除。

因此，a 和 b 都能被 5 整除。

这与 a 和 b 是互质整数的事实相矛盾，因为它们都有 5 作为公因子。

矛盾的出现是由于我们错误地假设 √5 是有理数。

因此，√5 是无理数。

2. 证明 3 + 2√5 是无理数。

解决方案

我们假设 3 + 2√5 是有理数。

因为 3 + 2√5 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得

但由于以下证明，√5 是无理数

（注意：学生在回答问题时不必添加以下证明，除非问题奖励的分数超过 3 分）

我们假设 √5 是有理数。

因为 √5 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得

√5 = a/b

b√5 = a

两边平方

5b² = a² …… (I)

从方程可以推断出 a² 被 5 整除，这进一步意味着 a 也能被 5 整除。

因此，我们可以写成

a = 5c，其中 c 是整数。

如果我们把 a 的值代入 (I)，我们得到

5b² = 25c²

b² = 5c²

从方程可以推断出 b² 被 5 整除，这进一步意味着 b 也能被 5 整除。

因此，a 和 b 都能被 5 整除。

这与 a 和 b 是互质整数的事实相矛盾，因为它们都有 5 作为公因子。

矛盾的出现是由于我们错误地假设 √5 是有理数。

因此，√5 是无理数。

从上面的证明可以清楚地看出 √5 是无理数。

这与 3 + 2√5 是有理数的假设相矛盾。因此，3 + 2√5 是无理数。

3. 证明以下是无理数

1. 1/√2
2. 7√5
3. 6 + √2

解决方案

I. 我们假设 √2 是有理数。

因为 √2 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得 √2 = a/b。

√2b = a

两边平方，我们得到

2b² = a² ……(I)

我们可以推断出 a² 被 2 整除，因此 a 也能被 2 整除。

因此，a = 2c，其中 c 是某个整数。

将 a 的值代入 (I)，我们得到

2b² = 4c²

b² = 2c²

这意味着 b² 被 2 整除，因此 b 也能被 2 整除。

因此，a 和 b 都有 2 作为公因子。

这与 a 和 b 是互质整数的事实相矛盾。

矛盾的出现是由于我们错误地假设 √2 是有理数。

因此，√2 是无理数。

这意味着 1/√2 也是无理数。

II. 我们假设 √5 是有理数。

因为 √5 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得

√5 = a/b

b√5 = a

两边平方

5b² = a² …… (I)

从方程可以推断出 a² 被 5 整除，这进一步意味着 a 也能被 5 整除。

因此，我们可以写成

a = 5c，其中 c 是整数。

如果我们把 a 的值代入 (I)，我们得到

5b² = 25c²

b² = 5c²

从方程可以推断出 b² 被 5 整除，这进一步意味着 b 也能被 5 整除。

因此，a 和 b 都能被 5 整除。

这与 a 和 b 是互质整数的事实相矛盾，因为它们都有 5 作为公因子。

矛盾的出现是由于我们错误地假设 √5 是有理数。

因此，√5 是无理数。

这意味着 7√5 也是无理数。

III. 我们假设 6 + √2 是有理数。

因为 6 + √2 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得 6 + √2 = a/b。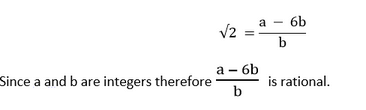

因此，√2 也是有理数。

但由于以下证明，√2 是无理数

（注意：学生在回答问题时不必添加以下证明，除非问题奖励的分数超过 3 分）

我们假设 √2 是有理数。

因为 √2 是有理数，所以存在两个互质整数 a 和 b；b ≠ 0，使得

√2 = a/b

b√2 = a

两边平方

2b² = a² …… (I)

从方程可以推断出 a² 被 2 整除，这进一步意味着 a 也能被 2 整除。

因此，我们可以写成

a = 2c，其中 c 是整数。

如果我们把 a 的值代入 (I)，我们得到

2b² = 4c²

b² = 2c²

从方程可以推断出 b² 被 2 整除，这进一步意味着 b 也能被 2 整除。

因此，a 和 b 都能被 2 整除。

这与 a 和 b 是互质整数的事实相矛盾，因为它们都有 2 作为公因子。

矛盾的出现是由于我们错误地假设 √2 是有理数。

因此，√2 是无理数。

从上面的证明可以清楚地看出 √2 是无理数。

这与 6 + √2 是有理数的假设相矛盾。因此，6 + √2 是无理数。

练习1.4

1. 不实际进行长除法，说明以下有理数将具有有限小数展开还是无限循环小数展开

1. 13/3125
2. 17/8
3. 64/455
4. 15/1600
5. 29/343
6. 23/2³5²
7. 129/2²5⁷7⁵
8. 6/15
9. 35/50
10. 77/210

解决方案

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数不能表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有无限循环小数展开。

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数不能表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有无限循环小数展开。

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数不能表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有无限循环小数展开。

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数可以表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有有限小数展开。

因为给定数不能表示为 p/q 的形式，其中 p 和 q 是互质的，而 q 的形式为 2ⁿ5^m。

因此，给定数具有无限循环小数展开。

2. 写出上面第 1 题中具有有限小数展开的有理数的十进制展开。

解决方案

第 1 题中的 I、II、IV、VI、VIII、IX 具有有限小数展开。这些可以计算如下：

乘以并除以 5³

乘以并除以 5⁴

乘以并除以 2

3. 以下实数具有如下给出的十进制展开。在每种情况下，判断它们是否是有理数。如果它们是有理数，并且是 p/q 的形式，那么关于 q 的质因数，你可以说什么？

1. 43.123456789
2. 0.120120012000120000. . .
3. 43.123456789

解决方案

I. 因为给定的十进制展开是有限的，所以它是理性的。

分母 q 可以表示为 2ⁿ5^m 的形式。

II. 因为给定的十进制展开是无限不循环的，所以它是有理数的，因此分母不能表示为 2ⁿ5^m。

III. 因为给定的十进制展开是无限循环的，所以它是有理数，但分母不能表示为 2ⁿ5^m 的形式。