NCERT 10年级数学第5章：等差数列

练习 5.1

1. 在下列哪种情况下，所涉及的数字列表构成一个等差数列，为什么？

1. 出租车每公里后的费用，当第一公里收费15卢比，每增加一公里收费8卢比时。
2. 当真空泵每次抽出气缸中剩余空气的1/4时，气缸中存在的空气量。
3. 挖井每米后的费用，当第一米费用为150卢比，之后每米增加50卢比时。
4. 每年账户中的金额，当存入10000卢比，年复合利率为8%时。

解决方案

I. 设n公里的出租车费为t_n。

已知，t₁ = 15

t₂ = 15 + 8

t₃ = 23 + 8

t₄ = 31 + 8

因为，t₄ - t₃ = t₃ - t₂ = t₂ - t₁

因此，给定情况构成一个等差数列。

II. 设t_n是使用n次真空泵后剩余的空气量。

设 t₁ = x

t₂ = x - ¼(x)

t₃ = ¾(x) - ¼(¾(x))

因为，t₃ - t₂ ≠ t₂ - t₁

因此，给定情况不构成等差数列。

III. 设挖n米的费用为t_n。

已知，t₁ = 150

t₂ = 150 + 50

t₃ = 200 + 50

t₄ = 250 + 50

因为，t₄ - t₃ = t₃ - t₂ = t₂ - t₁

因此，给定情况构成一个等差数列。

IV. 设n年的金额为t_n。

已知，t₁ = 10000

t₂ = 10000 + 10000 × 8/100

t₃ = 10800 + 10800 × 8/100

t₄ = 11664 + 11664 × 8/100

因为，t₄ - t₃ ≠ t₃ - t₂ ≠ t₂ - t₁

因此，给定情况不构成等差数列。

2. 当首项 a 和公差 d 如下给出时，写出等差数列的前四项。

1. a = 10, d = 10
2. a = -2, d = 0
3. a = 4, d = - 3
4. a = - 1, d = 1/2
5. a = - 1.25, d = - 0.25

解决方案

I. a = 10

a₂ = 10 + 10 = 20

a₃ = 20 + 10 = 30

a₄ = 30 + 10 = 40

前四项是10, 20, 30 和 40。

II. a = -2

a₂ = -2 + 0 = -2

a₃ = -2 + 0 = -2

a₄ = -2 + 0 = -2

前四项是-2, -2, -2 和 -2。

III. a = 4

a₂ = 4 - 3 = 1

a₃ = 1 - 3 = -2

a₄ = -2 - 3 = -5

前四项是4, 1, -2 和 -5。

IV. a = -1

a₂ = -1 + 1/2 = -1/2

a₃ = -1/2 + 1/2 = 0

a₄ = 0 + 1/2 = 1/2

前四项是-1, -1/2, 0 和 1/2。

V. a = -1.25

a₂ = -1.25 - 0.25 = -1.5

a₃ = -1.5 - 0.25 = -1.75

a₄ = -1.75 - 0.25 = -2.00

前四项是-1.25, -1.5, -1.75 和 -2。

3. 对于以下等差数列，写出首项和公差

1. 3, 1, - 1, - 3, . . .
2. - 5, - 1, 3, 7, . . .
3. 1/3, 5/3, 9/3, 13/3, . . .
4. 0.6, 1.7, 2.8, 3.9, . . .

解决方案

I. 首项 = a = 3

d = a₂ - a = 1 - 3 = -2

II. 首项 = a = -5

d = a₂ - a = -5 - (-1) = -4

III. 首项 = a = 1/3

d = a₂ - a = 5/3 - 1/3 = 4/3

IV. 首项 = a = 0.6

d = a₂ - a = 1.7 - 0.6 = 1.1

4. 下列哪些是等差数列？如果它们构成等差数列，找出公差d并写出另外三项。

1. 2, 4, 8, 16, . . .
2. 2, 5/2, 3, 7/2, . . .
3. 1.2, - 3.2, - 5.2, - 7.2, . . .
4. 10, - 6, - 2, 2, . . .
5. 3, 3 + √2, 3 + 2√2, 3 + 3√2, . . .
6. 0.2, 0.22, 0.222, 0.2222, . . .
7. 0, - 4, - 8, -12, . . .
8. -1/2, -1/2, -1/2, -1/2, . . .
9. 1, 3, 9, 27, . . .
10. a, 2a, 3a, 4a, . . .
11. a, a² , a³ , a⁴ , . . .
12. √2, √8, √18, √32, . . .
13. √3, √6, √9, √12, . . .
14. 1² , 3² , 5² , 7² , . . .
15. 1² , 3² , 5² , 73, . . .

解决方案

I. t₂ - t₁ = 4 - 2 = 2

t₃ - t₂ = 8 - 4 = 4

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

II. t₂ - t₁ = 5/2 - 2 = 1/2

t₃ - t₂ = 3 - 5/2 = 1/2

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = 2

公差 = d = ½

另外四项是

a₅ = 7/2 + ½ = 4

a₆ = 4 + ½ = 9/2

a₇ = 9/2 + ½ = 5

a₈ = 5 + ½ = 11/2

III. t₂ - t₁ = -3.2 - (-1.2) = -2

t₃ - t₂ = -5.2 - (-3.2) = -2

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = -1.2

公差 = d = -2

另外四项是

a₅ = -7.2 - 2 = -9.2

a₆ = -9.2 - 2 = -11.2

a₇ = -11.2 - 2 = -13.2

a₈ = -13.2 - 2 = -15.2

IV. t₂ - t₁ = -6 - (-10) = 4

t₃ - t₂ = -2 - (-6) = 4

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = -10

公差 = d = 4

另外四项是

a₅ = 2 + 4 = 6

a₆ = 6 + 4 = 10

a₇ = 10 + 4 = 14

a₈ = 14 + 4 = 18

V. t₂ - t₁ = 3 + √2 - 3 = √2

t₃ - t₂ = 3 + 2√2 - (3 + √2) = √2

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = 3

公差 = d = √2

另外四项是

a₅ = 3 + 3√2 + √2 = 3 + 4√2

a₆ = 3 + 4√2 + √2 = 3 + 5√2

a₇ = 3 + 5√2 + √2 = 3 + 6√2

a₈ = 3 + 6√2 + √2 = 3 + 7√2

VI. t₂ - t₁ = 0.22 - 0.2 = 0.02

t₃ - t₂ = 0.222 - 0.22 = 0.002

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

VII. t₂ - t₁ = -4 - 0 = -4

t₃ - t₂ = -8 - (-4) = -4

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = 0

公差 = d = -4

另外四项是

a₅ = -12 - 4 = -16

a₆ = -16 - 4 = -20

a₇ = -20 - 4 = -24

a₈ = -24 - 4 = -28

VIII. t₂ - t₁ = -1/2 - (-1/2) = 0

t₃ - t₂ = -1/2 - (-1/2) = 0

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = -1/2

公差 = d = 0

另外四项是

a₅ = -1/2 + 0 = -1/2

a₆ = -1/2 + 0 = -1/2

a₇ = -1/2 + 0 = -1/2

a₈ = -1/2 + 0 = -1/2

IX. t₂ - t₁ = 3 - 1 = 2

t₃ - t₂ = 9 - 3 = 6

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

X. t₂ - t₁ = 2a - a = a

t₃ - t₂ = 3a - 2a = a

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a₁ = a

公差 = d = a

另外四项是

a₅ = 4a + a = 5a

a₆ = 5a + a = 6a

a₇ = 6a + a = 7a

a₈ = 7a + a = 8a

XI. t₂ - t₁ = a² - a = a(a - 1)

t₃ - t₂ = a³ - a² = a² (a - 1)

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

XII. t₂ - t₁ = √8 - √2 = √2

t₃ - t₂ = √18 - √8= √2

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a = √2

公差 = d = √2

另外四项是

a₅ = √32 + √2 = √50

a₆ = √50 + √2 = √72

a₇ = √72 + √2 = √98

a₈ = √98 + √2 = √128

XIII. t₂ - t₁ = √6 - √3

t₃ - t₂ = √9 - √6

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

XIV. t₂ - t₁ = 3² - 1² = 8

t₃ - t₂ = 5² - 3² = 16

因为，t₃ - t₂ ≠ t₂ - t₁

因此，它不是一个等差数列。

XV. t₂ - t₁ = 5² - 1² = 24

t₃ - t₂ = 7² - 5² = 24

因为, t₃ - t₂= t₂ - t₁

因此，它是一个等差数列。

首项 = a₁ = 1²

公差 = d = 24

另外四项是

a₅ = 73 + 24 = 97

a₆ = 97 + 24 = 121 = 11²

a₇ = 121 + 24 = 145

a₈ = 145 + 24 = 169 = 13²

练习 5.2

1. 在下表中填空，已知 a 是首项，d 是公差，a_n 是等差数列的第 n 项。

解决方案

I. a_n = a + (n - 1)d

= 7 + 7(3) = 7 + 21 = 28

II. a_n = a + (n - 1)d

0 = -18 + 9d

18 = 9d

d = 2

III. a_n = a + (n - 1)d

-5 = a + (17)(-3)

-5 = a - 51

46 = a

IV. a_n = a + (n - 1)d

3.6 = -18.9 +(n - 1)2.5

22.5 = (n - 1)2.5

9 = n - 1

n = 10

V. a_n = a + (n - 1)d= 3.5 + 0 = 3.5

因此，完成的表格如下

2. 在以下选项中选择正确的答案并说明理由。

解决方案

I. 对于给定的等差数列, a = 10

并且

d = 7 - 10 = -3

a₃₀ = a + (n - 1)d

= 10 + 29(-3) = 10 - 87 = -77

因此，(C) 是正确答案。

II. 对于给定的等差数列, a = -3

并且

d = -1/2 - (-3) = -1/2 + 3 = 5/2

a₁₁ = a + (n - 1)d

= -3 + 10(5/2) = -3 + 25

= 22

因此，(B) 是正确答案。

3. 在下列等差数列中，找出方框中缺失的项。

解决方案

I. a = 2

a_n = a + (n - 1)d

a₃ = 26 = 2 + 2d

24 = 2d

d = 12

a₂ = a + 12 = 2 + 12 = 14

II. a₂ = 13, a₄ = 3

a₄ - a₃ = a₃ - a₂

3 - a₃ = a₃ - 13

16 = 2a₃

a₃ = 8

d = a₃ - a₂

= 8 - 13 = -5

a = a₂ - d = 13 - (-5) = 13 + 5 = 18

III. a = 5

a₄ = = 19/2

a_n = a + (n - 1)d

19/2 = 5 + 3d

9/2 = 3d

3/2 = d

a₂ = a + d = 5 + 3/2 = 13/2

a₃ = a + 2d = 5 + 2(3/2)

= 5 + 3 = 8

IV. a = -4

a₆ = 6

a_n = a + (n - 1)d

a₆ = -4 + 5d

6 = -4 + 5d

10 = 5d

d = 2

a₂ = a + d = -4 + 2 = -2

a₃ = a + 2d = -4 + 2(2) = 0

a₄ = a + 3d = -4 + 3(2) = 2

a₅ = a + 4d = -4 + 4(2) = 4

V. a₂ = 38 a₆ = -22

a_n = a + (n - 1)d

38 = a + d               … (I)

-22 = a + 5d               … (II)

从(II)中减去(I)

-22 - 38 = a + 5d - (a + d)

-60 = 4d

-15 = d

在(I)中使用 d = -15

38 = a - 15

53 = a

a₃ = a + 2d = 53 + 2(-15)

= 23

a₄ = a + 3d = 53 - 3(15) = 8

a₅ = a + 4d = 53 - 4(15) = -7

4. 等差数列 3, 8, 13, 18, . . . 的哪一项是 78？

解决方案

首项 = a = 3

公差 = d = 8 - 3 = 5

a_n = 78

a_n = a + (n - 1)d

78 = 3 + (n - 1)5

75 = (n - 1)5

15 = n - 1

n = 16

因此，78是给定等差数列的第16项。

5. 求下列各等差数列的项数

1. 7, 13, 19, . . . , 205
2. 18, , 13, . . . , - 47

解决方案

I. 首项 = a = 7

末项 = l = 205

公差 = d = 13 - 7 = 6

l = a + (n - 1)d

205 = 7 + (n - 1)6

198 = (n - 1)6

33 = n - 1

n = 34

因此，给定的等差数列有34项。

II. 首项 = a = 18

末项 = l = -47

公差 = d = 31/2 - 18 = -5/2

l = a + (n - 1)d

-47 = 18 + (n - 1)(-5/2)

-65 = (1 - n)(5/2)

-130 = (1 - n)5

-26 = 1 - n

n = 27

因此，给定的等差数列有27项。

6. 检查 -150 是否是等差数列 11, 8, 5, 2... 的一项

解决方案

我们假设-150是给定等差数列的一项。

首项 = a = 11

公差 = 8 - 11 = -3

a_n = -150

a_n = a + (n - 1)d

-150 = 11 + (n - 1)(-3)

-161 = (n - 1)(-3)

161/3 + 1 = n

164/3 = n

但这与n是自然数的事实相矛盾。

矛盾的产生是由于错误地假设-150是给定等差数列的一项。

7. 求一个等差数列的第31项，其第11项是38，第16项是73。

解决方案

a₁₁ = 38 a₁₆ = 73

a_n = a + (n - 1)d

38 = a + 10d               … (I)

73 = a + 15d               … (II)

从(II)中减去(I)

73 - 38 = a + 15d - (a + 10d)

35 = 5d

7 = d

在(I)中使用 d = 7

38 = a + 70

a = -32

a₃₁ = -32 + 30(7) = -32 + 210

a₃₁ = 178

8. 一个等差数列共有50项，其中第3项是12，最后一项是106。求第29项。

解决方案

a₅₀ = l = 106

a₃ = 12

a_n = a + (n - 1)d

106 = a + 49d               … (I)

12 = a + 2d               … (II)

从(I)中减去(II)

106 - 12 = a + 49d - (a + 2d)

94 = 47d

2 = d

在(II)中使用 d = 2

12 = a + 4

a = 8

a₂₉ = 8 + 28(2) = 8 + 56

a₂₉ = 64

9. 如果一个等差数列的第3项和第9项分别是4和-8，这个等差数列的哪一项是零？

解决方案

a₉ = -8

a₃ = 4

a_n = a + (n - 1)d

-8 = a + 8d               … (I)

4 = a + 2d               … (II)

从(I)中减去(II)

-8 - 4 = a + 8d - (a + 2d)

-12 = 6d

-2 = d

在(II)中使用 d = -2

4 = a - 4

a = 8

设第x项为0。

a_x = a + (x - 1)d

0 = 8 + (x - 1)(-2)

-8 = (x - 1)(-2)

4 = x - 1

x = 5

因此，等差数列的第5项是0。

10. 一个等差数列的第17项比第10项多7。求公差。

解决方案

a_n = a + (n - 1)d

a₁₇ - a₁₀ = 7

a + 16d - (a + 9d) = 7

7d = 7

d = 1

因此，给定等差数列的公差是1。

11. 等差数列 3, 15, 27, 39, . . . 的哪一项比它的第54项多132？

解决方案

设所求项为a_n。

首项 = a = 3

公差 = d = 15 - 3 = 12

a_n = a₅₄ + 132

a + (n - 1)d = a + 53d + 132

(n - 1)12 = 53(12) + 132

(n - 1) = 53 + 11

n - 1 = 64

n = 65

因此，给定等差数列的第65项将比其第54项多132。

12. 两个等差数列有相同的公差。它们第100项的差是100，它们第1000项的差是多少？

解决方案

A₁₀₀ - a₁₀₀ = 100

A + 99d - (a + 99d) = 100

A - a = 100

A₁₀₀₀ - a₁₀₀₀ = A + 999d - (a + 999d)

= A - a = 100

因此，它们第1000项的差是100。

13. 有多少个三位数能被7整除？

解决方案

能被7整除的3位数列表是

105, 112, …, 994

a = 105

d = 7

末项 = a + (n - 1)d

994 = 105 + (n - 1)7

889 = (n - 1)7

127 = n - 1

128 = n

因此，有128个三位数能被7整除。

14. 在10和250之间有多少个4的倍数？

解决方案

10和250之间4的倍数是

12, 16, 20, …, 248

a = 12

d = 4

末项 = a + (n - 1)d

248 = 12 + (n - 1)4

236 = (n - 1)4

59 = n - 1

n = 60

因此，在10和250之间有60个4的倍数。

15. 对于n的什么值，两个等差数列：63, 65, 67, . . . 和 3, 10, 17, . . . 的第n项相等？

解决方案

我们需要找到n使得A_n = a_n

A = 63 d₁ = 65 - 63 = 2

a = 3 d₂ = 10 - 3 = 7

A_n = a_n

A + (n - 1)d₁ = a + (n - 1)d₂

63 + (n - 1)2 = 3 + (n - 1)7

60 + 2n - 2 = 7n - 7

65 = 5n

n = 13

因此，给定等差数列的第13项是相等的。

16. 确定一个等差数列，其第三项是16，第七项比第五项多12。

解决方案

a₃ = 16

a₇ - a₅ = 12

a + 6d - (a + 4d) = 12

2d = 12

d = 6

a₃ = 16

a + 2d = 16

a + 2(6) = 16

a = 16 - 12

a = 4

a₂ = a + d = 4 + 6 = 10

因此，所求的等差数列是 4, 10, 16, …

17. 求等差数列 3, 8, 13, . . ., 253 的倒数第20项。

解决方案

将给定的等差数列反转

253, 248, …, 13, 8, 3

a_n = a + (n - 1)d

a = 253

d = 248 - 253 = -5

a₂₀ = a + 19d = 253 + 19(-5)

= 253 - 95

= 158

因此，倒数第20项将是158。

18. 一个等差数列的第4项和第8项之和是24，第6项和第10项之和是44。求该等差数列的前三项。

解决方案

a₄ + a₈ = 24

a₆ + a₁₀ = 44

a + 3d + a + 7d = 24

2a + 10d = 24

2 (a + 5d) = 24

a + 5d = 12 = a₆

a + 5d + a₁₀ = 44

a₁₀ + 12 = 44

a₁₀ = 32

从a₁₀中减去a₆

a₁₀ - a₆ = 32 - 12

a + 9d - (a + 5d) = 20

4d = 20

d = 5

在 a + 5d = 12 中使用 d = 5

a + 5(5) = 12

a + 25 = 12

a = -13

因此，首项 = -13，公差 = 5。

因此，前3项将是

a₁ = -13

a₂ = a + d = -13 + 5 = -8

a₃ = a + 2d = -13 + 2(5) = -13 + 10 = -3

19. Subba Rao于1995年开始工作，年薪为5000卢比，每年增加200卢比。他的收入在哪一年达到7000卢比？

解决方案

Subba Rao每年的工资可以表示为一个等差数列

5000, 5200, 5400, . . .

1995年的工资 = 首项 = a = 5000

每年增量 = 公差 = d = 200

a_n = a + (n - 1)d

a_n = 7000

7000 = 5000 + (n - 1)200

2000 = (n - 1)200

10 = n - 1

n = 11

等差数列中的第11项是7000。如果第一项代表1995年，那么第11项代表1995 + 10 = 2005年。

因此，Subba Rao的薪水在2005年达到了7000卢比。

20. Ramkali在某一年的第一周存了5卢比，然后每周储蓄增加1.75卢比。如果在第n周，她的周储蓄达到20.75卢比，求n。

解决方案

Ramkali每周的储蓄可以表示为一个等差数列

5, 6.75, 8.5, . . .

开始储蓄 = 首项 = a = 5

每周储蓄增量 = 公差 = d = 1.75

a_n = a + (n - 1)d

a_n = 20.75

20.75 = 5 + (n - 1)(1.75)

15.75 = (n - 1)(1.75)

9 = n - 1

10 = n

等差数列的第10项是20.75。

因此，Ramkali的储蓄在第10周达到了20.75卢比。

练习 5.3

1. 求下列等差数列的和

1. 2, 7, 12, . . ., 共10项。
2. -37, -33, -29, . . ., 共12项
3. 0.6, 1.7, 2.8, . . ., 共100项。
4. 1/15, 1/12 , 1/10, . . ., 共11项。

解决方案

因此，给定等差数列的和是245。

因此，给定等差数列的和是-180。

因此，给定等差数列的和是5505。

2. 求下面给出的和

1. 7 + + 14 + . . . + 84
2. 34 + 32 + 30 + . . . + 10
3. -5 + (-8) + (-11) + . . . + (-230)

解决方案

I. = a + (n - 1)d

a = 7, d = 21/2 - 7 = 7/2, a_n = 84

84 = 7 + (n - 1)7/2

77 = (n - 1)7/2

22 = n - 1

n = 23

因此，给定等差数列的和是1046.5

II. a_n = a + (n - 1)d

a = 34, d = 32 - 34 = -2, a_n = 10

10 = 34 + (n - 1)(-2)

-24 = (n - 1)(-2)

12 = n - 1

n = 13

因此，给定等差数列的和是286。

III. a_n = a + (n - 1)d

a = -5, d = -8 - (-5) = -3, a_n = -230

-230 = -5 + (n - 1)(-3)

-225 = (n - 1)(-3)

75 = n - 1

n = 76

因此，给定等差数列的和是-8930。

3. 在一个等差数列中

1. 已知 a = 5, d = 3, a_n = 50, 求 n 和 S_n。
2. 已知 a = 7, a₁₃ = 35, 求 d 和 S₁₃。
3. 已知 a₁₂ = 37, d = 3, 求 a 和 S₁₂。
4. 已知 a₃ = 15, S₁₀ = 125, 求 d 和 a₁₀。
5. 已知 d = 5, S₉ = 75, 求 a 和 a₉。
6. 已知 a = 2, d = 8, S_n = 90, 求 n 和 a_n。
7. 已知 a = 8, a_n = 62, S_n = 210, 求 n 和 d。
8. 已知 a_n = 4, d = 2, S_n = -14, 求 n 和 a。
9. 已知 a = 3, n = 8, S = 192, 求 d。
10. 已知 l = 28, S = 144, 共有9项。求 a。

解决方案

a_n = a + (n - 1)d

50 = 5 + (n - 1)3

45 = (n - 1)3

15 = n - 1

n = 16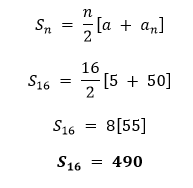

因此，n = 16 且 S_n = 490。

II.

a_n = a + (n - 1)d

a₁₃ = 7 + (13 - 1)d

35 = 7 + 12d

28 = 12d

7/3 = d

因此，d = 7/3 且 S₁₃ = 273。

III.

a_n = a + (n - 1)d

a₁₂ =a + (12 - 1)3

37 = a + 33

a = 4

因此，a = 4 且 S₁₂ = 490。

IV.

a_n = a + (n - 1)d

a₃ = a + (3 - 1)d

15 = a + 2d               … 方程式 (I)

d = -1

在方程式 (I) 中使用 d = -1

15 = a + 2(-1)

15 = a - 2

17 = a

a₁₀ = a + (10 - 1)d

= 17 + 9(-1)

= 17 - 9 = 8

a₁₀ = 8

因此，d = -1 且 a₁₀ = 8。

V.

a₉ = a + (9 - 1)d

a₉ = -35/3 + 8(5)

a₉ = -35/3 + 40

a₉ = 85/3

因此，a = -35/3 且 a₉ = 85/3。

VI.

但 n 必须是一个正整数，所以 n = -9/2 被舍弃。

因此，n = 5。

a₅ = a + (5 - 1)d

= 2 + 4(8) = 2 + 32 = 34

a₅ = 34

因此，n = 5 且 a_n = 34。

VII.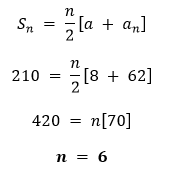

a_n = a + (n - 1)d

a₆ = 8 + (6 - 1)d

62 = 8 + 5d

54 = 5d

d = 54/5

因此，n = 6 且 d = 54/5。

VIII.

a_n = a + (n - 1)d

4 = a + (n - 1)2

4 = a + 2n - 2

6 = a + 2n

a = 6 - 2n

但 n 必须是一个正整数，所以 n = -2 被舍弃。

因此，n = 7。

a = 6 - 2n = 6 - 2(7)

= 6 - 14

a = -8

因此，n = 7 且 a = -8。

IX.

因此，d = 6。

X.

因此，a = 4。

4. 等差数列：9, 17, 25, ... 必须取多少项才能使和为 636？

解决方案

首项 = a = 9

公差 = 17 - 9 = 8

但是，n必须是正整数，所以n = -53/4被舍弃。因此，n = 12。

因此，必须取给定等差数列的12项才能得到636的和。

5. 一个等差数列的首项是5，末项是45，和是400。求项数和公差。

解决方案

首项 = a = 5

末项 = l = 45

l = a₁₆ = 45

a_n = a + (n - 1)d

a₁₆ = 5 + (16 - 1)d

45 = 5 + 15d

40 = 15d

d = 8/3

因此，该等差数列的项数是16，公差是8/3。

6. 一个等差数列的首项和末项分别为17和350。如果公差是9，那么有多少项，它们的和是多少？

解决方案

首项 = a = 17

末项 = l = a_n = 350

公差 = d = 9

a_n = a + (n - 1)d

350 = 17 + (n - 1)9

333 = (n - 1)9

37 = n - 1

n = 38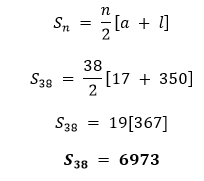

因此，该等差数列包含38项，其和为6973。

7. 求一个等差数列前22项的和，其中 d = 7，第22项是149。

解决方案

a₂₂ = 149

公差 = d = 7

a_n = a + (n - 1)d

a₂₂ = a + (22 - 1)7

149 = a + 21(7)

149 = a + 147

a = 2

因此，给定等差数列的前22项之和为1661。

8. 求一个等差数列前51项的和，其第二项和第三项分别为14和18。

解决方案

公差 = d = a₃ - a₂

d = 18 - 14 = 4

a_n = a + (n - 1)d

a₂ = a + d

14 = a + 4

a = 10

9. 如果一个等差数列的前7项之和是49，前17项之和是289，求前n项之和。

解决方案

a₉ - a₄ = a + 8d - (a + 3d)

17 - 7 = a + 8d - a - 3d

10 = 5d

d = 2

在 a + 3d = 7 中使用 d = 2

a + 3(2) = 7

a + 6 = 7

a = 1

因此，给定等差数列的前n项之和为n²。

10. 证明 a₁, a₂ , . . ., a_n , . . . 形成一个等差数列，其中 a_n 定义如下

1. a_n = 3 + 4n
2. a_n = 9 - 5n

并求出每种情况下前15项的和。

解决方案

I. a_n = 3 + 4n

a₁ = 3 + 4(1) = 3 + 4 = 7

a₂ = 3 + 4(2) = 3 + 8 = 11

a₃ = 3 + 4(3) = 3 + 12 = 15

a₂ - a₁ = 11 - 7 = 4

a₃ - a₂ = 15 - 11 = 4

因为 a₂ - a₁ = a₃ - a₂，所以给定的序列是一个公差 d = 4 的等差数列。

a₁₅ = 3 + 4(15) = 3 + 60 = 63

因此，给定等差数列的前15项之和为525。

II. a_n = 9 - 5n

a₁ = 9 - 5(1) = 9 - 5 = 4

a₂ = 9 - 5(2) = 9 - 10 = -1

a₃ = 9 - 5(3) = 9 - 15 = -6

a₂ - a₁ = -1 - 4 = -5

a₃ - a₂ = -6 - (-1) = -5

因为 a₂ - a₁ = a₃ - a₂，所以给定的序列是一个公差 d = -5 的等差数列。

a₁₅ = 9 - 5(15) = 9 - 75 = -66

因此，给定等差数列的前15项之和为-465。

11. 如果一个等差数列的前n项之和是 4n - n²，那么首项（即S₁）是什么？前两项之和是多少？第二项是什么？同样地，求出第3项、第10项和第n项。

解决方案

已知

S_n = 4n - n²

首项 = a = S₁

S₁ = 4(1) - (1)² = 4 - 1

S₁ = a = 3

前两项之和 = S₂

S₂ = 4(2) - (2)² = 8 - 4

S₂ = 4

S₂ = a + a₂

4 = 3 + a₂

a₂ = 1

因此，第二项是1。

S₃ = 4(3) - (3)² = 12 - 9 = 3

S₃ = S₂ + a₃

3 = 4 + a₃

a₃ = -1

因此，第三项是-1。

S₉ = 4(9) - (9)² = 36 - 81 = -45

S₁₀ = 4(10) - (10)² = 40 - 100 = -60

S₁₀ = S₉ + a₁₀

-60 = -45 + a₁₀

a₁₀ = -15

因此，第10项是-15。

类似地，

S_n = S_{n - 1} + a_n

a_n = S_n - S_{n - 1}

a_n = 4n - n² - [4(n - 1) - (n - 1)²]

a_n = 4n - n² - [4n - 4 - (n² + 1 - 2n)]

a_n = 4n - n² - (6n - 5 - n²)

a_n = 5 - 2n

因此，第n项是5 - 2n。

12. 求前40个能被6整除的正整数之和。

解决方案

前40个能被6整除的正整数列表可以表示为一个等差数列

6 × 1, 6 × 2, 6 × 3, … … , 6 × 40

6, 12, 18, … … , 240

首项 = a = 6

公差 = d = 6

a₄₀ = 240

因此，前40个能被6整除的正整数之和是4920。

13. 求前15个8的倍数之和。

解决方案

前15个8的倍数列表构成一个等差数列

8 × 1, 8 × 2, 8 × 3, … … , 8 × 15

8, 16, 24, … … , 120

首项 = a = 8

公差 = d = 8

a₁₅ = 120

因此，前15个8的倍数之和是4920。

14. 求0到50之间奇数的和。

解决方案

0到50之间的奇数列表构成一个等差数列

1, 3, 5, … …, 49

首项 = a = 1

末项 = l = 49

公差 = d = 2

a_n = a + (n - 1)d

49 = 1 + (n - 1)2

48 = (n - 1)2

24 = n - 1

n = 25

因此，0到50之间奇数的和是625。

15. 一项建筑工程合同规定，超过某个日期完成工程将受到罚款，具体如下：第一天罚款200卢比，第二天罚款250卢比，第三天罚款300卢比，等等，每一天的罚款比前一天多50卢比。如果承包商延误了30天，他需要支付多少罚款？

解决方案

延期罚款构成一个等差数列

200, 250, 300, … …

首项 = a = 200

公差 = d = 50

a_n = a + (n - 1)d

n = 30

a₃₀ = 200 + (30 - 1)(50)

a₃₀ = 200 + 29(50)

a₃₀ = 200 + 1450

a₃₀ = 1650

30天的罚款 = S₃₀

因此，承包商因延误30天需要支付27750卢比的罚款。

16. 一笔700卢比的款项将用于向学校的学生颁发七个现金奖，以表彰他们的综合学业表现。如果每个奖项比前一个奖项少20卢比，求每个奖项的价值。

解决方案

每个奖项的价值可以表示为一个等差数列

a, a - 20, a- 2(20), … …, a - 6(20)

a, a - 20, a - 40, … …, a - 120

给定等差数列的和 = S₇ = 700

a₁ = 160

a₂ = 160 - 20 = 140

a₃ = 140 - 20 = 120

a₄ = 120 - 20 = 100

a₅ = 100 - 20 = 80

a₆ = 80 - 20 = 60

a₇ = 60 - 20 = 40

因此，七个奖项的价值分别为160卢比、140卢比、120卢比、100卢比、80卢比、60卢比、40卢比。

17. 在一所学校里，学生们想在学校内外植树以减少空气污染。决定每个班级的每个班将种植的树木数量与他们所在的班级相同，例如，一年级的一个班将种植1棵树，二年级的一个班将种植2棵树，以此类推，直到十二年级。每个年级有三个班。学生们将种植多少棵树？

解决方案

每个年级3个班种植的树木数量可以表示为一个等差数列

3 × 1, 3 × 2, 3 × 3, … …, 3 × 12

3, 6, 9, … …, 36

首项 = a = 3

公差 = d = 6 - 3 = 3

末项 = a₁₂ = 36

学生们种植的树木总数 = S₁₂

因此，学生们种植的树木总数为234棵。

18. 一个螺旋由连续的半圆组成，圆心交替在A和B，从A开始，半径分别为0.5厘米，1.0厘米，1.5厘米，2.0厘米，...如图5.4所示。由十三个连续半圆组成的这种螺旋的总长度是多少？（取π = 22/7）。

[提示：连续半圆的长度为 l₁, l₂ , l₃ , l₄ , . . . 圆心分别在 A, B, A, B, . . ., ]

解决方案

设半径表示为 R₁, R₂, R₃, … …, R₁₃。

螺旋形成的半圆半径为

0.5, 1, 1.5, 2.0, … …

半径构成一个等差数列，其中，

首项 = a = 0.5

公差 = 1 - 0.5 = 0.5

n = 13

所有半径之和 = S₁₃

圆的周长 = 2πR

半圆的周长 = 2πR/2 = πR

给定螺旋的长度 = L = πR₁ + πR₂ + πR₃ + … … + πR₁₃

L = π(R₁ + R₂ + R₃ + … … + R₁₃)

L = π(S₁₃)

L = (45.5)22/7

L = 143

因此，给定螺旋的长度是143厘米。

19. 200根原木按以下方式堆放：最底层20根，上一层19根，再上一层18根，依此类推（见图5.5）。这200根原木被放在多少行中，顶层有多少根原木？

解决方案

每行原木的数量可以表示为一个等差数列

20, 19, 18, … …

第一行原木数 = a = 20

公差 = d = -1

总原木数 = S = 200

当 n = 25 时，a_n = a + (25 - 1)d

= 20 + 24(-1) = 20 - 24

= -4

但是，最后一行的原木数量不可能是负数，所以n = 25被舍弃。因此，n = 16。

a_n = a + (16 - 1)d

= 20 + 15(-1) = 20 - 15

= 5

因此，顶层的原木数量是5根，行数是16行。

20. 在一次土豆赛跑中，一个桶放在起点，距离第一个土豆5米，其他土豆每隔3米放在一条直线上。线上有十个土豆（见图5.6）。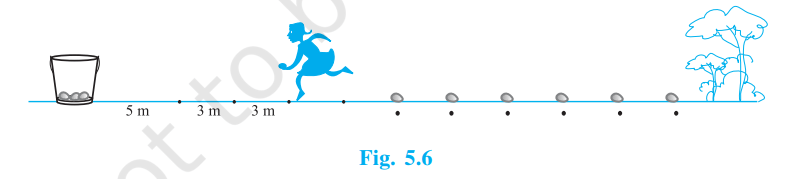

一个参赛者从桶出发，捡起最近的土豆，跑回去放进桶里，再跑去捡下一个土豆，跑到桶里放下，她以同样的方式继续，直到所有土豆都在桶里。参赛者总共需要跑多远？

[提示：捡起第一个和第二个土豆，参赛者跑的总距离（米）是 2 × 5 + 2 × (5 + 3)]

解决方案

第一个土豆离桶的距离 = 5m

第二个土豆离桶的距离 = 5 + 3 = 8m

第三个土豆离桶的距离 = 8 + 3 = 11m

土豆离桶的距离构成一个等差数列

5, 8, 11, … … 共10项

首项 = a = 5

公差 = d = 3

参赛者捡起土豆后必须跑回桶边。

因此，总距离 = 2 × [每个土豆离桶的距离之和]

= 2 × [S₁₀]

参赛者跑的总距离 = 2 × 185 = 370m。

练习 5.4 (选做)

1. 等差数列 121, 117, 113, . . . 的哪一项是它的第一个负数项？

[提示：求 a_n < 0 时的 n]

解决方案

首项 = a = 121

公差 = d = 117 - 121 = -4

因为，所求项是负数。

因此，a_n < 0。

因此，给定等差数列的第32项将是其第一个负数项。

2. 一个等差数列的第三项和第七项之和为6，它们的积为8。求该等差数列前十六项的和。

解决方案

已知 a₃ + a₇ = 6

且 a₃ × a₇ = 8

a + 2d + a + 6d = 6

2a + 8d = 6

2(a + 4d) = 6

a + 4d = 3 = a₅

a = 3 - 4d

(a + 2d) (a + 6d) = 8

使用 a = 3 - 4d

(3 - 4d + 2d) (3 - 4d + 6d) = 8

(3 - 2d) (3 + 2d) = 8

3² - (2d)² = 8

9 - 4d² = 8

1 = 4d²

¼ = d²

d = ± ½

因此, a = 3 - 4(± ½)

a = 3 - 2 = 1

或

a = 3 + 2 = 5

情况I： a = 1 且 d = ½

情况II： a = 5 且 d = -½

因此，给定等差数列的前16项之和是76或20。

3. 一个梯子有相隔25厘米的横档。（见图5.7）。横档的长度从底部的45厘米均匀递减到顶部的25厘米。如果顶部和底部的横档相距 米，制作横档需要多长的木材？

[提示：横档数量 = 250/25 + 1]

解决方案

每个横档相距25厘米，第一个和最后一个横档之间的距离是5/2米 = 250厘米。

因此，横档数量 = 250/25 + 1 = 10 + 1 = 11

由于每个横档的长度均匀递减，它将形成一个等差数列，其中

首项 = a = 45

末项 = a₁₁ = 25

制作横档所需的木材长度 = S_n

因此，制作横档所需的木材总长度为385厘米。

4. 一排房子的门牌号从1到49连续编号。证明存在一个值x，使得编号为x的房子之前的房子门牌号之和等于其后的房子门牌号之和。找出这个x的值。

[提示：S_x - 1 = S₄₉ - S_x ]

解决方案

门牌号构成一个等差数列

1, 2, 3, … …, 49

首项 = a = 1

公差 = d = 1

末项 = a₄₉ = 49

x之前的房子门牌号之和 = S_{x - 1}

x之后的房子门牌号之和 = S₄₉ - S_x

但是，门牌号x必须在1到49之间，所以x = -35被舍弃。

因此，x = 35。

5. 一个足球场的小露台由15级台阶组成，每级台阶长50米，由实心混凝土建造。每级台阶高¼米，宽½米。（见图5.8）。计算建造这个露台所需的混凝土总体积。

[提示：建造第一级台阶所需的混凝土体积 = ¼ × ½ × 50 m³]

解决方案

每级台阶从底部开始的高度增加¼米，所以它形成一个等差数列

¼, ¼ + ¼, ¼ + ¼ + ¼, … …, 共15项

¼, ½, ¾, … … …, 共15项

首项 = a = ¼

公差 = d = ¼

每级台阶所需的混凝土体积 = 高度 × 宽度 × 长度

台阶宽度 = ½ m (固定)

台阶长度 = 50 m (固定)

建造第一级台阶所需的混凝土体积 = ¼ × ½ × 50 m³ = a × ½ × 50

建造第二级台阶所需的混凝土体积 = (¼ + ¼) × ½ × 50 m³ = a₂ × ½ × 50

因此，露台所需的混凝土总体积是

= (a × ½ × 50) + (a₂ × ½ × 50) + … … + (a₁₅ × ½ × 50)

= ½ × 50 × [a + a₂ + … … + a₁₅]

= ½ × 50 × [S₁₅]

所需混凝土总体积 = ½ × 50 × [30]

= 750 m³

因此，建造这个露台需要750立方米的混凝土。