NCERT 10年级数学

第四章：一元二次方程

练习 4.1

1. 检查以下哪些是一元二次方程

1. (x + 1)² = 2(x - 3)
2. x² - 2x = (-2) (3 - x)
3. (x - 2)(x + 1) = (x - 1)(x + 3)
4. (x - 3)(2x +1) = x(x + 5)
5. (2x - 1)(x - 3) = (x + 5)(x - 1)
6. x² + 3x + 1 = (x - 2)²
7. (x + 2)³ = 2x (x² - 1)
8. x³ - 4x² - x + 1 = (x - 2)³

解决方案

I.

(x + 1)² = 2(x - 3)
x² + 1 + 2x = 2x - 6
x² + 7 = 0

因为x的最高次数是2。因此，给定的方程是一元二次方程。

II.

x² - 2x = -2(3 - x)
x² - 2x = 2x - 6
x² - 4x + 6 = 0

因为x的最高次数是2。因此，给定的方程是一元二次方程。

III.

(x - 2)(x + 1) = (x - 1)(x + 3)
x² + x - 2x - 2 = x² - x + 3x - 3
x² - x - 2 = x² + 2x - 3
0 = 3x - 1

因为x的最高次数是1。因此，给定的方程不是一元二次方程。

IV.

(x - 3)(2x + 1) = x(x + 5)
2x² + x - 6x - 3 = x² + 5x
x² - 5x - 3 = 5x
x² - 10x - 3 = 0

因为x的最高次数是2。因此，给定的方程是一元二次方程。

V.

(2x - 1)(x - 3) = (x - 1)(x + 5)
2x² - 6x - x + 3 = x² + 5x - x - 5
x² - 7x + 3 = 4x - 5
x² - 11x + 8 = 0

因为x的最高次数是2。因此，给定的方程是一元二次方程。

VI.

x² + 3x + 1 = (x - 2)²
x² + 3x + 1 = x² - 4x + 4
7x - 3 = 0

因为x的最高次数是1。因此，给定的方程不是一元二次方程。

VII.

(x + 2)^3 = 2x(x² - 1)
x^3 + 8 + 6x² + 12x = 2x^3 - 2x
0 = x^3 - 6x² - 14x - 8

因为x的最高次数是3。因此，给定的方程不是一元二次方程。

VIII.

x^3 - 4x^(2 )- x + 1 = (x - 2)^3
x^3 - 4x² - x + 1 = x^3 - 6x² + 12x - 8
2x² - 13x + 9 = 0

因为x的最高次数是2。因此，给定的方程是一元二次方程。

2. 用一元二次方程的形式表示以下情况

1. 一个矩形地块的面积是528平方米。地块的长度（以米为单位）比其宽度的两倍多1。我们需要找到地块的长度和宽度。
2. 两个连续正整数的乘积是306。我们需要找到这两个整数。
3. 罗汉的母亲比他大26岁。3年后，他们年龄的乘积将是360。我们想找到罗汉现在的年龄。
4. 一列火车以匀速行驶480公里。如果速度每小时慢8公里，那么覆盖相同距离将需要多3小时。我们需要找到火车的速度。

解决方案

I. 设矩形地块的宽度为x（以米为单位）。

已知地块的长度比宽度的两倍多1，

因此，矩形地块的长度 = 2x + 1

我们知道：

矩形面积 = 长 × 宽

因此，所需的方程将是

528 = x(2x + 1)
528 = 2x² + x
2x² + x - 528 = 0

II. 设较小的整数为x。

已知这两个整数是连续的，

因此另一个整数是 = x + 1。

已知这两个整数的乘积是306。

因此，所需的方程将是

306 = x(x + 1)
306 = x² + x
x² + x - 306 = 0

III. 设罗汉现在的年龄（以年为单位）为x。

那么，他母亲现在的年龄（以年为单位）= x + 26。

已知3年后他们年龄的乘积将是360。

因此，所需的方程将是
(x + 3)(x + 26 + 3) = 360
x² + 26x + 3x + 3x + 78 + 9 = 360
x² + 32x + 87 = 360
x² + 32x - 273 = 0

IV. 设火车的速度（以公里/小时为单位）为x。

我们知道：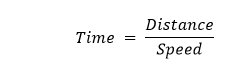

利用这个知识，我们可以得出火车所需的时间 = 480/x

已知将火车的速度每小时降低8公里，将需要多3小时才能完成行程。

因此，所需的方程将是

练习 4.2

1. 通过因式分解求解以下一元二次方程的根

1. x² - 3x - 10 = 0
2. 2x² + x - 6 = 0
3. √2x² + 7x + 5√2 = 0
4. 2x² - x + 1/8 = 0
5. 100x² - 20x + 1 = 0

解决方案

I.

x² - 3x - 10 = 0
x² - 5x + 2x - 10 = 0
x(x - 5) + 2(x - 5) = 0
(x - 5)(x + 2) = 0
x - 5 = 0
⇒ x = 5

或

x + 2 = 0
⇒ x = -2

因此，给定方程的根是5和-2。

II.

2x² + x - 6 = 0
2x² + 4x - 3x - 6 = 0
2x(x + 2) - 3(x + 2) = 0
(x + 2)(2x - 3) = 0
2x - 3 = 0
2x = 3
⇒ x = 3/2

或

x + 2 = 0
⇒ x = -2

因此，给定方程的根是3/2和-2。

III.

因此，给定方程的根是-5/√2和-√2。

IV.

因此，给定方程的根是¼和¼。

V.

因此，给定方程的根是1/10和1/10。

2. 求解例1中的问题。

(供参考) 例1中的问题

1. 约翰和吉万蒂总共有45颗弹珠。他们都各丢了5颗弹珠，他们现在拥有的弹珠数量的乘积是124。我们想找出他们开始时有多少颗弹珠。
2. 一家乡村工业每天生产一定数量的玩具。每个玩具的生产成本（以卢比为单位）被发现是55减去一天生产的玩具数量。在某一天，总生产成本为750卢比。我们想找出那天生产了多少个玩具。

解决方案

I. 设约翰开始时拥有的弹珠数量为x。

那么吉万蒂开始时拥有的弹珠数量将是45 - x。

已知他们都丢了4颗弹珠，弹珠的乘积变为124。因此

(x - 5)(45 - x - 5) = 124
-(x - 4)(x - 40) = 124
x² - 40x - 5x + 160 = -124
x² - 45x + 324 = 0
x² - 9x - 36x + 324 = 0
x(x - 9) - 36(x - 9) = 0
(x - 9)(x - 36) = 0
x - 9 = 0
⇒ x = 9
45 - x = 45 - 9 = 36
或
x - 36 = 0
⇒ x = 36
45 - x = 45 - 36 = 9

因此，约翰和吉万蒂分别拥有9颗和36颗弹珠，或者分别拥有36颗和9颗弹珠。

II. 设乡村工业每天生产的玩具数量为x。

那么，每个玩具的生产成本（以卢比为单位）= 55 - x

已知在某一天，总生产成本为750卢比。因此

因此，给定日期乡村工业生产的玩具数量为25或30。

3. 找到两个数，它们的和是27，积是182。

解决方案

设这两个数中的一个为x。

那么，另一个数将是 = 27 - x

已知这两个数的乘积是182。因此，

x(27 - x) = 182
27x - x² = 182
x² - 27x + 182 = 0
x² - 14x - 13x + 182 = 0
x(x - 14) - 13(x - 14 )= 0
(x - 14)(x - 13) = 0
x - 14 = 0
⇒ x = 14
27 - x = 27 - 14 = 13
或
x - 13 = 0
⇒ x = 13
27 - x = 27 - 13 = 14

因此，这两个数分别是13和14，或者分别是14和13。

4. 找出两个连续的正整数，它们的平方和是365。

解决方案

设较小的正整数为x。

那么另一个正整数 = x + 1

已知这两个数的平方和是365。因此，

(x² ) + (x + 1)² = 365
x² + x² + 2x + 1 = 365
2x² + 2x - 364 = 0
2(x² + x - 182) = 0
x² + 14x - 13x - 182 = 0
x(x + 14) - 13(x + 14) = 0
(x + 14)(x - 13) = 0
x + 14 = 0
⇒ x = -14
或
x - 13 = 0
⇒ x = 13

但是，题目要求整数是正数。因此，x = -14 被拒绝。

因此，所需的正整数是13和13 + 1 = 14。

5. 直角三角形的高比其底短7厘米。如果斜边是13厘米，求另外两条边。

解决方案

设直角三角形的底（厘米）为x。

那么，直角三角形的高（厘米）= x - 7

斜边 = 13厘米（已知）

根据勾股定理，

底² + 高² = 斜边²

因此，

x² + (x - 7)² = 13²
x² + x² + 49 - 14x = 169
2x² - 14x - 120 = 0
2(x² - 7x - 60) = 0
x² - 12x + 5x - 60 = 0
x(x - 12) + 5(x - 12) = 0
(x - 12)(x + 5) = 0
x + 5 = 0
⇒ x = -5
或
x - 12 = 0
⇒ x = 12

但是，x是长度，永远不能为负。因此，x = -15 被拒绝。

因此，给定直角三角形的底是12厘米，高是12 - 7 = 5厘米。

6. 一个乡村工业每天生产一定数量的陶器。在某一天，观察到每个文章的生产成本（以卢比为单位）比当天生产的文章数量的两倍多3。如果当天总生产成本为90卢比，找出生产的文章数量和每篇文章的成本。

解决方案

设乡村工业每天生产的陶器数量为x。

那么，每件陶器的生产成本（以卢比为单位）= 2x + 3

已知在某一天，总生产成本为90卢比。因此

x(2x + 3) = 90

(每天生产的文章数量 × 每篇文章的成本 = 总成本)

2x² + 3x = 90
2x² + 3x - 90 = 0
2x² + 15x - 12x - 90 = 0
x(2x + 15) - 6(2x + 15) = 0
(2x + 15)(x - 6) = 0
x - 6 = 0
⇒ x = 6
或
2x + 15 = 0
2x = 15

但是，生产的文章数量不能是分数。因此，x = 15/2 被拒绝。

因此，给定日期乡村工业生产的文章数量是6，每篇文章的成本是90/6 = 15卢比。

练习 4.3

1. 用配方法求以下一元二次方程的根

1. 2x² - 7x + 3 = 0
2. 2x² + x - 4 = 0
3. 4x² + 4√3x + 3 = 0
4. 2x² + x + 4 = 0

解决方案

I.

2x² - 7x + 3 = 0

我们需要x²的系数为1。所以，我们将两边都除以2。

在左边加上并减去(7/4)²。

因此，根是x = ½ 和 x = 3。

II.

2x² + x - 4 = 0

我们需要x²的系数为1。所以，我们将两边都除以2。

在左边加上并减去(1/4)²。

因此，根是x = -√3/2 和 x = -√3/2。

IV.

2x² + x + 4 = 0

我们需要x²的系数为1。所以，我们将两边都除以2。

在左边加上并减去(1/4)²。

√(-31) 是一个虚数。

因此，对于给定的二次方程，根不是实数。

2. 通过应用二次公式求解上面Q.1中给出的一元二次方程的根。

(供参考) 问题1中的方程

1. 2x² - 7x + 3 = 0
2. 2x² + x - 4 = 0
3. 4x² + 4 √3x + 3 = 0
4. 2x² + x + 4 = 0

解决方案

I. 将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 2, b = -7, c = 3

计算判别式

d = b² - 4ac
d = (-7)² - 4(2)(3)
d = 49 - 24
d = 25

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

因此，根是3和½。

I. 将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 2, b = 1, c = -4

计算判别式

d = b² - 4ac
d = (1)² - 4(2)(-4)
d = 1 + 32
d = 33

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

III. 将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 4, b = 4√3, c = 3

计算判别式

因为d = 0。

因此，对于给定的方程存在两个相等且实数根α和β。

IV. 将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 2, b = 1, c = 4

计算判别式

d = b² - 4ac
d = (1)² - 4(2)(4)
d = 1 - 32
d = -31

因为d < 0。

因此，对于这个方程不存在实数根。

3. 求以下方程的根

1. x - 1/x = 3, x ≠ 0
2. 1/(x + 4) - 1/(x - 7) = 11/30, x ≠ -4, 7

解决方案

I.

两边乘以x。

x² - 1 = 3x

x² - 3x - 1 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -3, c = -1

计算判别式

d = b² - 4ac
d = (-3)² - 4(1)(-1)
d = 9 + 4
d = 13

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -3, c = 2

计算判别式

d = b² - 4ac
d = (-3)² - 4(1)(2)
d = 9 - 8
d = 1

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

因此，根是2和1。

4. 雷曼3年前和5年后的年龄（以年为单位）的倒数之和是1/3。求他的现年年龄。

解决方案

设雷曼现在的年龄（以年为单位）为x。

他3年前年龄的倒数 = 1/(x - 3)

他5年后年龄的倒数 = 1/(x + 5)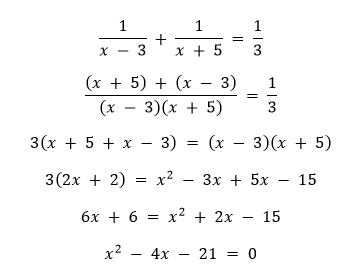

将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 1, b = -4, c = 21

计算判别式

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

因为年龄不能为负，所以x = -3被拒绝。

因此，雷曼现在的年龄（以年为单位）是x = 7。

5. 在一次课堂测验中，谢法莉在数学和英语上的总分是30。如果她在数学上多得2分，在英语上少得3分，那么她们的分数乘积将是210。找出她在两门学科上的分数。

解决方案

设谢法莉在数学上的得分为x。

那么，谢法莉在英语上的得分 = 30 - x。

已知如果她在数学上多得2分，在英语上少得3分，那么分数的乘积将是210。因此

(x + 2)(30 - x - 3) = 210
(x + 2)(27 - x) = 210
27x - x² + 54 - 2x = 210
-x² + 25x + 54 - 210 = 0
x² - 25x + 156 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -25, c = 156

计算判别式

d = b² - 4ac
d = (-25)² - 4(1)(156)
d = 625 - 624
= 1

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

当x = 12时，

30 - x = 30 - 12 = 18

当x = 13时，

30 - x = 30 - 13 = 17

因此，谢法莉在数学上得到13分，在英语上得到17分；或者在数学上得到12分，在英语上得到18分。

6. 一个矩形地块的对角线比短边长60米。如果长边比短边长30米，求地块的边长。

解决方案

设矩形地块的长（米）为x。

那么矩形地块的短边（米）= x - 30

矩形的对角线 = 60 + (x - 30)

矩形的对角线和两条边构成一个直角三角形。

根据勾股定理，

斜边² = 底² + 高²
(60 + x - 30)² = x² + (x - 30)²
(x + 30)² = x² + (x - 30)²
x² + 900 + 60x = x^(2 )+ (x² + 900 - 60x)
120x = x²
120 = x

短边 = x - 30 = 120 - 30 = 90 m

因此，矩形地块的长边是120米，短边是90米。

7. 两个数的平方差是180。较小数的平方是较大数的8倍。求这两个数。

解决方案

设较大数为x。

那么较小数的平方 = 8x

因为两个数的平方差是180。因此

x² - 8x = 180
x² - 8x - 180 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -8, c = -180

计算判别式

d = b² - 4ac
d = (-8)² - 4(1)(-180)
d = 64 + 720
d = 784

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

但是，x不能为负，因为这将导致较小数的平方为负，这是不可能的。因此，x = 18。

8. 一列火车以匀速行驶360公里。如果速度每小时快5公里，那么相同的行程将需要少1小时。求火车的速度。

解决方案

设火车的速度（以公里/小时为单位）= x。

行驶距离 = 360公里

我们知道：

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = 5, c = -1800

计算判别式

d = b² - 4ac
d = (5)² - 4(1)(-1800)
d = 25 + 7200
d = 7225

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

9. 两个水龙头一起可以在 小时内注满一个水箱。较大的直径的水龙头单独注满水箱需要比较小的水龙头少10小时。找出每个水龙头可以单独注满水箱的时间。

解决方案

设较大直径水龙头注满水箱所需的时间（小时）= x

那么较小直径水龙头注满水箱所需的时间（小时）= x + 10

较小直径水龙头每小时注满水箱的水量 = 1/(x + 10)

较大直径水龙头每小时注满水箱的水量 = 1/x

已知如果两个水龙头可以共同在 小时内注满水箱 = 75/8。因此

将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 4, b = -35, c = -375

计算判别式

d = b² - 4ac
d = (-35)² - 4(4)(-375)
d = 1225 + 6000
d = 7225

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

但是所需时间不能为负，所以x = -25/4被拒绝。

因此x = 15

因此，较大直径水龙头所需的时间 = 15小时

较小直径水龙头所需的时间 = 15 + 10 = 25小时。

10. 一列特快列车在迈索尔和班加罗尔之间以132公里的路程比普通列车少花1小时（不考虑它们在中途停靠的时间）。如果特快列车的平均速度比普通列车快11公里/小时，求两列车的平均速度。

解决方案

设普通列车的平均速度（公里/小时）= x。

那么特快列车的平均速度（公里/小时）= x + 11

普通列车行驶132公里所需时间 = 132/x

特快列车行驶132公里所需时间 = 132/(x + 11)

已知特快列车少花1小时完成行程。因此

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = 11, c = -1452

计算判别式

d = b² - 4ac
d = (11)² - 4(1)(-1452)
d = 121 + 5808
d = 5929

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

但是火车的速度不能为负，所以x = -44被拒绝。

因此，普通列车的平均速度 = 33公里/小时

特快列车的平均速度 = 33 + 11 = 44公里/小时

11. 两个正方形的面积之和是468平方米。如果它们的周长之差是24米，求两个正方形的边长。

解决方案

设较大正方形的边长（米）= x

较小正方形的周长 = 4x - 24

那么较小正方形的边长 = (4x - 24)/4 = x - 6

已知两个正方形的面积之和为468平方米，因此

x² + (x - 6)² = 468
x² + 36 + x² - 12x = 468
2x² - 12x - 432 = 0
2(x² - 6x - 216) = 0
x² - 6x - 216 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -6, c = -198

计算判别式
d = b² - 4ac
d = (-6)² - 4(1)(-216)
d = 36 + 864
d = 900

因为d > 0。

因此，对于给定的方程存在两个实根α和β。

但是，长度不能为负，所以x = -4被拒绝。

因此，较大正方形的边长 = 18米，

较小正方形的边长 = x - 6 = 18 - 6 = 12米。

练习 4.4

1. 求以下一元二次方程根的性质。如果存在实根，则求出它们

1. 2x² - 3x + 5 = 0
2. 3x² - 4 √ 3 x + 4 = 0
3. 2x² - 6x + 3 = 0

解决方案

I. 将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 2, b = -3, c = 5

计算判别式

d =? b?² - 4ac
d = (-3)² - 4(2)(5)
d = 9 - 40
d = -31

因为d < 0。

给定方程的根将是虚数。

II. 将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 3, b = -4√3, c = 4

计算判别式

d = b² - 4ac
d = (-4√3)² - 4(3)(4)
d = 48 - 48
d = 0

因为d = 0。

给定方程的根将是实数且相等。

III. 将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 2, b = -6, c = 3

计算判别式

因为d > 0。

给定方程的根将是实数。

2. 对于以下每个一元二次方程，求k的值，使它们有两个相等的根。

1. 2x² + kx + 3 = 0
2. kx (x - 2) + 6 = 0

解决方案

I. 因为已知给定的方程有相等的根。因此，判别式为0。

将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = 2, b = k, c = 3

II. kx(x - 2) + 6 = 0

kx² - 2kx + 6 = 0

因为已知给定的方程有相等的根。因此，判别式为0。

将给定的二次方程与ax² + bx + c = 0进行比较，我们得到

a = k, b = -2k, c = 6

d = b² - 4ac
0 = (-2k)² - 4(k)(6)
0 = 4k² - 24k
24k = 4k²
24 = 4k
k= 6

3. 是否有可能设计一个矩形芒果林，其长度是其宽度的两倍，面积是800平方米？如果可能，求出其长度和宽度。

解决方案

设所需的矩形芒果林的长度为x米。

那么其宽度 = x/2 米。

矩形面积 = 长 × 宽

但是长度不能为负，所以x = -40被拒绝。

因此，矩形芒果林的长度 = 40米，

矩形芒果林的宽度 = 40/2 = 20米。

4. 以下情况是否可能？如果可能，确定他们的现年年龄。

两个朋友的年龄之和是20岁。四年前，他们年龄的乘积是48。求他们的现年年龄。

解决方案

设一个朋友现在的年龄（以年为单位）= x。

那么另一个朋友现在的年龄 = 20 - x。

四年前，两个朋友的年龄分别是(x - 4)和(20 - x - 4)。

已知4年前他们年龄的乘积是48。因此

(x - 4)(16 - x) = 48
16x - x² - 64 + 4x = 48
-x² + 20x - 64 - 48 = 0
x² - 20x + 112 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -20, c = 112

计算判别式

d = b² - 4ac
d = (-20)² - 4(1)(112)
d = 400 - 448
d = -48

因为d < 0。

给定方程的根不存在。

因此，给定的情况是不可能的。

5. 是否有可能设计一个周长为80米，面积为400平方米的矩形公园？如果可能，求出其长度和宽度。

解决方案

设矩形公园的长度为x米。

矩形公园的周长 = 80

80 = 2(长) + 2(宽)

80 - 2x = 2(宽)

那么，矩形场地的宽度 = (80 - 2x)/2 = 40 - x

面积 = 长 × 宽

400 = x(40 - x)
400 = 40x - x²
x² - 40x + 400 = 0

将给定的二次方程与ax2 + bx + c = 0进行比较，我们得到

a = 1, b = -40, c = 400

计算判别式

d = b² - 4ac
d = (-40)² - 4(1)(400)
d = 1600 - 1600
d = 0

因为d = 0。

因此，对于给定的方程，根是实数且相等。

因此，矩形公园的长度 = 20米。

矩形公园的宽度 = 40 - x = 40 - 20 = 20米。