NCERT 10年级数学第12章解决方案：与圆有关的面积

练习 12.1

除非另有说明，否则使用 π = 22/7

1. 两个圆的半径分别为19厘米和9厘米。求周长等于两个圆周长之和的圆的半径。

解决方案

设所求圆的半径为 x。

第一个圆的周长 = 2πR = 2 × 22/7 × 19

= 836/7 厘米

第二个圆的周长 = 2πr = 2 × 22/7 × 9

= 396/7 厘米

第三个圆的周长 = 2πR + 2πr = 836/7 + 396/7 厘米

= 1232/7 厘米

2πx = 1232/7

2 × 22x/7 = 1232/7

44x = 1232

x = 28 厘米

因此，所求圆的半径为28厘米。

2. 两个圆的半径分别为8厘米和6厘米。求面积等于两个圆面积之和的圆的半径。

解决方案

设所求圆的半径为 x。

第一个圆的面积 = πR² = 22/7 × 8²

= 22/7 × 64 = 1408/7 平方厘米

第二个圆的面积 = πr² = 22/7 × 6²

= 792/7 厘米

第三个圆的面积 = πR² + πr² = 1408/7 + 792/7 平方厘米

= 2200/7 厘米

πx² = 2200/7

22(x²)/7 = 2200/7

22x² = 2200

x² = 100

x = 10 厘米

因此，所求圆的半径为10厘米。

3. 图12.3描绘了一个射箭靶，其五个得分区域从中心向外标记为金、红、蓝、黑和白。代表金色得分的区域的直径为21厘米，其他每个条带的宽度为10.5厘米。求五个得分区域的面积。

解决方案

I. 金色区域半径 = r₁ = 21/2 = 10.5 厘米

金色区域面积 = r₂ = πr₁²

= 22/7 × (10.5)² = 22/7 × 110.25

= 22(15.75) = 346.5 平方厘米

II. 到红色区域的半径 = r₂ = 10.5 + 10.5 = 21 厘米

红色区域面积 = πr₂² - πr₁²

= 22/7 × 21² - 346.5

= 22(63) - 346.5

= 1386 - 346.5 = 1039.5 平方厘米

III. 到蓝色区域的半径 = r₃ = 21 + 10.5 = 31.5 厘米

蓝色区域面积 = πr₃² - πr₂²

= 22/7 × (31.5)² - 1386

= 22(141.75) - 1386

= 3118.5 - 1386 = 1732.5 平方厘米

IV. 到黑色区域的半径 = r₄ = 31.5 + 10.5 = 42 厘米

黑色区域面积 = πr₄² - πr₃²

= 22/7 × (42)² - 3118.5

= 22(252) - 3118.5

= 5544 - 3118.5 = 2425.5 平方厘米

V. 到白色区域的半径 = r₅ = 42 + 10.5 = 52.5 厘米

白色区域面积 = πr₅² - πr₄²

= 22/7 × (52.5)² - 5544

= 22(393.75) - 5544

= 8662.5 - 5544 = 3118.5 平方厘米

4. 一辆汽车的轮子直径均为80厘米。当汽车以每小时66公里的速度行驶时，每个轮子在10分钟内转多少整圈？

解决方案

汽车每小时行驶的距离 = 66公里 = 66000米

汽车每分钟行驶的距离 = 66000/60 = 1100米

汽车在10分钟内行驶的距离 = 1100 × 10 = 11000米

每个轮子的半径 = 80/2 = 40厘米 = 0.4米

每个轮子在一次旋转中覆盖的距离 = 2πr

= 2 × 22/7 × 0.4 = 17.6/7 米

覆盖11000米所需的转数 = 11000/(17.6/7)

= 11000(7)/17.6 = 7000/1.6

= 4375

因此，当汽车以每小时66公里的速度行驶时，每辆汽车的轮子在10分钟内完成4375次整圈旋转。

5. 在下列选项中勾选正确答案并说明理由：如果一个圆的周长和面积在数值上相等，那么这个圆的半径是

(A) 2 单位 (B) π 单位 (C) 4 单位 (D) 7 单位

解决方案

圆的面积 = 圆的周长

πr² = 2πr

r² = 2r

r = 2 单位

因此，(A) 是正确答案。

练习 12.2

除非另有说明，否则使用 π = 22/7

1. 求半径为6厘米的圆的扇形面积，如果扇形角为60°。

解决方案

给定圆的扇形角 = 60°

扇形面积 = (θ/360°) × πr²

= (60°/360°) × 22/7 × 6²

= 1/6 × 22/7 × 6²

= 22/7 × 6

= 132/7 平方厘米

2. 求周长为22厘米的圆的象限面积。

解决方案

给定圆的周长 = 22 厘米

2πr = 22

2 × 22/7 × r = 22

2r = 7

r = 7/2 厘米

圆的象限面积 = (1/4) × πr²

= 1/4 × 22/7 × (7/2)²

= 11/2 × 7/4

= 77/8 平方厘米

3. 钟表的分钟指针长度为14厘米。求分钟指针在5分钟内扫过的面积。

解决方案

钟表分钟指针的长度 = r = 14 厘米

分钟指针在60分钟内扫过的面积 = πr²

= 22/7 × 14²

= 22 × 2 × 14

= 616 平方厘米

分钟指针在60分钟内覆盖的角度 = 360°

分钟指针在5分钟内覆盖的角度 = 360°/60° × 5 = 30°

钟表分钟指针在5分钟内扫过的面积 = (θ/360°) × πr²

= (30°/360°) × 616

= 1/12 × 616

= 154/3 平方厘米

4. 半径为10厘米的圆的一条弦在圆心处张成一个直角。求相应部分的面积：(i) 小弓形 (ii) 大扇形。(使用 π = 3.14)

解决方案

圆的半径 = 10 厘米

圆面积 = πr²

= 3.14 × 10² = 314 平方厘米

(i) 小弓形面积 = (θ/360°) × πr²

= (90°/360°) × 314

= 1/4 × 314

= 76 平方厘米

(ii) 大弓形面积 = ((360° - θ)/360°) × πr²

= (270°/360°) × 314

= 3/4 × 314

= 228 平方厘米

5. 在半径为21厘米的圆中，一条弧在圆心处张成60°角。求

1. 弧的长度
2. 由弧形成的扇形面积
3. 由相应弦形成的弓形面积

解决方案

(i) 圆的周长 = 2πr = 2 × 22/7 × 21

= 2 × 22 × 3

= 132 厘米

弧长 = (θ/360°) × 2πr

= (60°/360°) × 132

= 1/6 × 132

= 22 厘米

(ii) 圆的面积 = πr²

= 22/7 × 21²

= 22 × 3 × 21

= 1386 平方厘米

由弧形成的扇形面积 = (θ/360°) × πr²

= 1/6 × 1386

= 231 平方厘米

(iii) 弓形面积 = 扇形面积 - △AOB面积

= 231 - √3/4 × r² (AOB是等边三角形，因为两条边相等，夹角为60°)

= 231 - √3/4 × 21²

= 231 - 441√3/4

= (924 - 441√3)/4 平方厘米

6. 半径为15厘米的圆的一条弦在圆心处张成60°角。求圆的相应小弓形和大弓形的面积。(使用 π = 3.14 和 √3 = 1.7)。

解决方案

圆面积 = πr²

= 3.14 × 15²

= 3.14 × 225

= 706.5 平方厘米

扇形面积 = (θ/360°) × πr²

= (60°/360°) × 706.5

= 1/6 × 706.5

= 706.5/6 平方厘米

小弓形面积 = 扇形面积 - △AOB面积

由于两条边相等（都是同一圆的半径）且夹角为60°，所以AOB是等边三角形。

小弓形面积 = 706.5/6 - √3/4 × 15²

= 706.5/6 - 1.73/4 × 225

= 706.5/6 - 97.31

= 122.64/6

= 20.44 平方厘米

大弓形面积 = 圆的面积 - 小弓形面积

= 706.5 - 20.44 = 686.06 平方厘米

7. 半径为12厘米的圆的一条弦在圆心处张成120°角。求相应弓形部分的面积。(使用 π = 3.14 和 √3 = 1.73)。

解决方案

圆面积 = πr²

= π × 12²

= 144π 平方厘米

扇形面积 = (θ/360°) × πr²

= (120°/360°) × 144π

= 1/3 × 144π

= 48π 平方厘米

弓形面积 = 扇形面积 - △AOB面积

画OD ⊥ AB。

AOB是等腰三角形，因为有两条边相等（都是同一圆的半径）。因此，垂直于第三边的线段将充当∠O的角平分线。

在AOB中，我们有

sin O = AD/OA

sin 60° = AD/12

√3/2 = AD/12

6√3 厘米 = AD

同样，BD = 6√3 厘米。

AB = 12√3 厘米。

另外，cos O = OD/OA (在AOB中)

cos 60° = OD/12

1/2 = OD/12

6 厘米 = OD

AOB面积 = 1/2 × 12√3 × 6

= 36√3 厘米

弓形面积 = 48π - 36√3

= 48(3.14) - 36(1.73)

=150.72 - 62.28

= 88.44 平方厘米

因此，相应弓形部分的面积为88.44平方厘米。

8. 一匹马被一条5米长的绳子拴在一个边长为15米的方形草地的角落（见图12.11）。求

1. 马可以吃草的那部分草地的面积。
2. 如果绳子长10米而不是5米，草地面积的增加量。(使用 π = 3.14)

解决方案

马可以吃草的区域是一个半径等于绳子长度的圆的四分之一。

(i) 由绳子形成的圆的面积 = πr²

= (3.14)5²

= (3.14)25

= 78.5 平方米

马可以吃草的草地面积 = 1/4 × πr²

= 1/4 × 78.5

= 19.625 平方米

(ii) 由新绳子长度形成的圆的面积 = πR²

= (3.14)10²

= (3.14)100

= 314 平方米

马可以吃草的草地面积 = 1/4 × πR²

= 1/4 × 314

= 78.5 平方米

当绳子长度增加到10米时，草地面积的增加量 = πR² - πr²

= 78.5 - 19.625

= 58.875 平方米

9. 一枚胸针由银丝制成，呈圆形，直径为35毫米。这些银丝也用于制作5根直径，将圆分成10个相等的扇形，如图12.12所示。求

1. 所需的银丝总长度。
2. 胸针每个扇形的面积。

解决方案

(i) 用于制作直径的导线长度 = 35 × 5 = 175毫米 = 17.5厘米

用于制作圆的导线长度 = 2πr

= 2 × 22/7 × 35/20

= 2 × 22/7 × 1.75

= 44 × 0.25

= 11 厘米

胸针中使用的导线总长度 = 11 厘米。

(ii) 圆形胸针的面积 = πr²

= 22/7 × (1.75)²

= 22 × 0.25 × 1.75

= 9.625 平方厘米

每个扇形的面积 = 1/10 × πr²

= 1/10 × 9.625

= 0.9625 平方厘米 或 96.25 平方毫米

因此，每个扇形的面积为96.25平方毫米。

10. 一把雨伞有8根等距分布的伞骨（见图12.13）。假设雨伞是一个半径为45厘米的平面圆，求雨伞两根连续伞骨之间的面积。

解决方案

假设雨伞是一个平面圆，伞骨将其分成8个面积相等的扇形。扇形的面积将是两根连续伞骨之间的面积。

圆面积 = πr²

= 22/7 × 45²

= 22/7 × 2025

= 6364.29 平方厘米

每个扇形的面积 = 1/8 × πr²

= 1/8 × 6364.29

= 795.5 平方厘米

因此，雨伞两根连续伞骨之间的面积为795.5平方厘米。

11. 一辆汽车有两个不重叠的雨刮器。每个雨刮器的刮片长度为25厘米，扫过角度为115°。求每次刮扫时被清理的总面积。

解决方案

每个雨刮器扫过的面积可以想象成一个圆。

这个圆的半径 = 25 厘米

每个雨刮器扫过360°角的面积 = 圆的面积

= πr²

= 22/7 × 25²

= 22/7 × 625

= 1964.29 平方厘米

每个雨刮器扫过115°角的面积 = (θ/360°) × πr²

= (115°/360°) × πr²

= 23/72 × 1964.29

= 627.48 平方厘米

雨刮器扫过的总面积 = 2(627.48)

= 1254.96 平方厘米

因此，刮片每次扫过的总面积为1254.96平方厘米。

12. 为警示船只注意水下礁石，灯塔以80°角向16.5公里距离散布红色灯光。求船只被警示的海面面积。(使用 π = 3.14)

解决方案

灯光覆盖的区域可以想象成一个圆。

圆的半径 = 16.5 公里

圆的面积 = πr²

= (3.14) × (16.5)²

= 854.87 平方公里

扇形面积 = (θ/360°) × πr²

= (80°/360°) × 854.87

= 2/9 × 854.87

= 189.971 平方公里

因此，船只被警示的海面面积为189.97平方公里。

13. 一个圆形桌布上有六个相同的图案，如图12.14所示。如果桌布的半径为28厘米，求图案的制作成本，费率为每平方厘米0.35。(使用 √3 = 1.7)

解决方案

我们需要将每个图案的边缘连接到圆心。

圆面积 = πr²

= 22/7 × 28²

= 22 × 4 × 28

= 2464 平方厘米

一个扇形的面积 = 1/6 × πr²

= 1/6 × 2464

= 1232/3 平方厘米

由于圆有六个相等的扇形，因此每个扇形的角度 = 360°/6

= 60°

△AOB有两条相等边（都是同一圆的半径）且夹角为60°，因此AOB是等边三角形。

AOB的面积 = √3/4 × r²

= √3/4 × 28²

= √3 × 7 × 28

= 196√3 平方厘米

每个图案的面积 = 相应小弓形的面积

= 扇形面积 - AOB面积

= 1232/3 - 196√3

= (1232 - 588√3)/3

= (1232 - 999.6)/3

= 232.4/3 平方厘米

六个图案的面积 = 6 × 232.4/3 = 464.8 平方厘米

制作1平方厘米图案的成本 = 0.35卢比

制作464.8平方厘米图案的成本 = 0.35 × 464.8 卢比

= 162.68 卢比

因此，桌布上图案的制作成本为162.68卢比。

14. 在下列选项中勾选正确答案。

半径为R的圆，角度为p（以度为单位）的扇形的面积是

(A) p/180 × 2πR (B) p/180 × π R² (C) p/360 × 2πR (D) p/720 × 2πR²

解决方案

扇形面积 = (θ/360°) × πR²

= p/360 × πR²

(A) = p/180 × 2πR = p/90 × πR，所以(A)是错误的。

(B) = p/180 × πR²，所以(B)是错误的。

(C) = p/360 × 2πR = p/180 × πR，所以(C)是错误的。

(D) = p/720 × 2πR² = p/360 × πR²，所以(D)是正确的。

因此，正确答案是 (D)。

练习 12.3

除非另有说明，否则使用 π = 22/7。

1. 如图12.19所示，求阴影区域的面积，如果PQ = 24厘米，PR = 7厘米，O是圆心。

解决方案

∠P是半圆内角，由直径所张。因此，它是直角。

这意味着PQR是直角三角形，QR是斜边。

通过在PQR中应用勾股定理，我们得到

QR² = PQ² + PR²

QR² = 24² + 7²

QR² = 576 + 49

QR² = 625

QR = 25 厘米

圆的半径 = 25/2 = 12.5 厘米

半圆面积 = πr²/2

= 22/7 × 12.5² × 1/2

= 11/7 × 156.25

= 245.54 平方厘米

PQR的面积 = 1/2 × PQ × PR

= 1/2 × 24 × 7

= 84 平方厘米

阴影区域面积 = 半圆面积 - PQR面积

= 245.54 - 84

= 161.54 平方厘米

因此，阴影区域的面积为161.54平方厘米。

2. 如图12.20所示，求阴影区域的面积，如果两个同心圆的半径分别为7厘米和14厘米，中心为O，且∠AOC = 40°。

解决方案

小圆的面积 = πr²

= 22/7 × 7²

= 22 × 7

= 154 平方厘米

大圆的面积 = πR²

= 22/7 × 14²

= 22 × 2 × 14

= 616 平方厘米

BOD扇形的面积 = (θ/360°) × πr²

= (40°/360°) × 154

= 1/9 × 154

= 154/9 平方厘米

AOC扇形的面积 = (θ/360°) × πR²

= 1/9 × 616

= 616/9 平方厘米

阴影区域面积 = AOC面积 - BOD面积

= 616/9 - 154/9

= 462/9

= 51.33 平方厘米

因此，阴影区域的面积为51.33平方厘米。

3. 如图12.21所示，求阴影区域的面积，如果ABCD是边长为14厘米的正方形，APD和BPC是半圆。

解决方案

AD = BC = 14厘米（已知）

由于APD和BPC是相同半径的半圆，因此它们的面积也相等。

两个半圆的面积 = 2 × (πr²)/2

= 22/7 × 14/2 × 14/2

= 22 × 7

= 154 平方厘米

正方形ABCD的面积 = s² = 14² = 196 平方厘米

阴影区域面积 = ABCD面积 - 两个半圆的面积

= 196 - 154

= 42 平方厘米

因此，阴影区域的面积为42平方厘米。

4. 如图12.22所示，其中以边长为12厘米的等边三角形OAB的顶点O为圆心，画出了半径为6厘米的圆弧。求阴影区域的面积。

解决方案

圆面积 = πr²

= 22/7 × 6²

= 792/7 平方厘米

三角形的面积 = √3/4 × a²

= √3/4 × 12²

= 36√3 平方厘米

图形的总面积 = 圆的面积 + 三角形的面积

= 792/7 + 36√3 平方厘米

三角形和圆有重叠区域。

重叠面积 = 小扇形的面积

= (θ/360°) × πr²

= (60°/360°) × πr²

= 1/6 × 792/7

= 132√3 平方厘米

阴影区域面积 = 总面积 - 重叠面积

= 792/7 + 36√3 - 132/7

= 660/7 + 36√3 平方厘米

因此，阴影区域的面积为(660/7 + 36√3)平方厘米。

5. 从边长为4厘米的正方形的每个角处切下一个半径为1厘米的圆的四分之一，并剪下一个直径为2厘米的圆，如图12.23所示。求正方形剩余部分的面积。

解决方案

正方形的面积 = s²

= 4² = 16 平方厘米

正方形内的圆的面积 = πr²

= 22/7 × (2/2)²

= 22/7 × 1 × 1

= 22/7 平方厘米

每个角的圆的四分之一的面积 = 4 × πr² × 1/4

= 22/7 平方厘米

阴影区域面积 = 正方形面积 - 4个四分之一的面积 - 圆的面积

= 16 - 22/7 - 22/7

= 16 - 44/7

= (112 - 44)/7

= 68/7 平方厘米

因此，正方形的剩余面积为68/7平方厘米。

6. 在半径为32厘米的圆形桌布中，形成了一个图案，中间留下了等边三角形ABC（如图12.24所示）。求图案的面积。

解决方案

我们需要在三角形ABC中画出中线AD。

AO = 32 厘米

由于ABC是外接圆的等边三角形，因此中心O将与三角形的质心重合。

AO = 2/3 AD，因为质心将中线分成2:3的比例。

AD = 3/2 AO

= 3/2 × 32 = 48 厘米

我们知道等边三角形的中线也是垂直平分线。因此，通过在ABD中使用勾股定理

AB² = AD² + BD²

AB² = 48² + (AB/2)²

AB² = 2304 + AB²/4

3/4 AB² = 2304

AB² = 768 × 4

AB² = 3072

AB = 32√3 平方厘米

三角形的面积 = √3/4 × a²

= √3/4 × (32√3)²

= √3/4 × 3072

= 768√3 平方厘米

圆面积 = πr²

= 22/7 × 32²

= 22528/7 平方厘米

图案面积 = 圆的面积 - 三角形的面积

= 22528/7 - 768√3 平方厘米

因此，桌布上图案的面积为(22528/7 - 768√3)平方厘米。

7. 如图12.25所示，ABCD是边长为14厘米的正方形。以A、B、C、D为圆心，画四个圆，使得每个圆都与其余三个圆中的两个相切。求阴影区域的面积。

解决方案

由于正方形的所有角都是90°。因此，正方形中有4个相等圆的四分之一。

一个四分之一的面积 = 1/4 × πr²

4个四分之一的面积 = 4 × 1/4 × πr²

= 22/7 × (14/2)²

= 22 × 7

= 154 平方厘米

正方形的面积 = s²

= 14² = 196 平方厘米

阴影区域面积 = 正方形面积 - 4个四分之一的面积

= 196 - 154

= 42 平方厘米

因此，阴影区域的面积为42平方厘米。

8. 图12.26描绘了一个赛道，其左侧和右侧端部是半圆形的。

两条内平行线段之间的距离为60米，每条长度为106米。如果赛道宽度为10米，求

1. 沿着内边缘的赛道周围的距离
2. 赛道的面积。

解决方案

AB = CD = PQ = RS = 106 米

CR = DS = 60 米

AC = BD = PR = QS = 10 米

(i) 半圆的半径 = CR/2 = 60/2 = 30 米

两个半圆的赛道长度 = 2πr

= 2 × 22/7 × 30

= 1320/7 米

内侧赛道的总距离 = 两个半圆的周长 + RS + CD

= 1320/7 + 106 + 106

= 1320/7 + 212

= (1320 + 1484)/7

= 2804/7 米

(ii) ABCD的面积 = AB × AC

= 106 × 10

= 1060 平方米

AB = PQ 且 AC = PR，因此 PQRS的面积 = ABCD的面积 = 1060平方米

2个外半圆的面积 = πR²

= 22/7 × (60 + 10 + 10)²/2²

= 22/7 × 1600

= 35200/7 平方米

2个内半圆的面积 = πr²

= 22/7 × 30²

= 19800/7 平方米

赛道的面积 = 2 × ABCD面积 + 2个外半圆的面积 - 2个内半圆的面积

= 2 × 1060 + 35200/7 - 19800/7

= 2120 + 15400/7

= 2120 + 2200

= 4320 平方米

9. 如图12.27所示，AB和CD是圆（中心为O）的两个互相垂直的直径，OD是小圆的直径。如果OA = 7厘米，求阴影区域的面积。

解决方案

可以注意到OA、OB、OC和OD是圆的半径，因此相等。

大圆的面积 = πR²

= 22/7 × 7²

= 154 平方厘米

OD是小圆的直径。

小圆的面积 = πr²

= 22/7 × 7/2 × 7/2

= 77/2 平方厘米

AB = OB + OA = 7 + 7 = 14 厘米

△ABC的面积 = 1/2 × 底 × 高

= 1/2 × AB × OC

= 1/2 × 14 × 7

= 49 平方厘米

阴影区域面积 = 小圆的面积 + 1/2 × 大圆的面积 - △ABC的面积

= 77/2 + 1/2 × 154 - 49

= 77/2 + 77 - 49

= 77/2 + 28

= (77 + 56)/2

= 133/2

= 66.5 平方厘米

因此，阴影区域的面积为66.5平方厘米。

10. 等边三角形ABC的面积为17320.5平方厘米。以三角形的每个顶点为中心，画一个半径等于三角形边长一半的圆（见图12.28）。求阴影区域的面积。(使用 π = 3.14 和 √3 = 1.73205)

解决方案

等边三角形的面积 = √3/4 × s²

17320.5 = √3/4 × s²

17320.5 = 1.73205/4 × s²

10000 × 4 = s²

40000 = s²

s = 200 厘米

每个圆的半径 = s/2 = 100 厘米

每个圆的小扇形面积 = (θ/360°) × πr²

= (60°/360°) × 3.14 × 100²

= 1/6 × 31400

= 15700/3 平方厘米

阴影区域面积 = 三角形面积 - 3 × 每个圆的小扇形面积

= 17320.5 - 3 × 15700/3

= 17320.5 - 15700

= 1620.5 平方厘米

因此，阴影区域的面积为1620.5平方厘米。

11. 在一块方形手帕上，制作了九个半径为7厘米的圆形图案（见图12.29）。求手帕剩余部分的面积。

解决方案

手帕边长 = 3 × 一个圆形图案的直径

= 3 × 7(2)

= 3 × 14

= 42 厘米

手帕的面积 = 42² = 1764 平方厘米

一个圆形图案的面积 = πr²

= 22/7 × 7²

= 154 平方厘米

手帕的剩余面积 = 手帕的面积 - 9 × 一个圆形图案的面积

= 1764 - 9 × 154

= 1764 - 1386

= 378 平方厘米

12. 如图12.30所示，OACB是以O为中心，半径为3.5厘米的圆的四分之一。如果OD = 2厘米，求

(i) 象限OACB， (ii) 阴影区域的面积。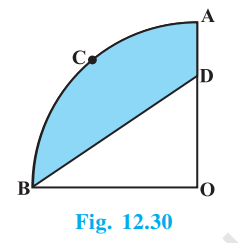

解决方案

(i) 象限OACB的面积 = 1/4 × πr²

= 1/4 × 22/7 × (3.5)²

= 77/8 平方厘米

= 9.625 平方厘米

(ii) △OBD的面积 = 1/2 × 底 × 高

= 1/2 × OB × OD

= 1/2 × 3.5 × 2

= 3.5 平方厘米

阴影区域面积 = 象限OACB的面积 - △OBD的面积

= 9.625 - 3.5

= 6.125 平方厘米

13. 如图12.31所示，一个正方形OABC内接于象限OPBQ。如果OA = 20厘米，求阴影区域的面积。(使用 π = 3.14)

解决方案

连接O与B。

OAB是直角三角形，因此通过应用勾股定理，我们得到

OB² = OA² + AB²

OB² = 20² + 20²

OB² = 400 + 400

OB² = 800

OB = 20√2 厘米

OB是给定圆的象限的半径。

象限的面积 = 1/4 × πr²

= 1/4 × 3.14 × (20√2)²

= 1/4 × 3.14 × 800

= 628 平方厘米

正方形OABC的面积 = OA²

= 20² = 400 平方厘米

阴影区域面积 = 象限面积 - 正方形面积

= 628 - 400

= 228 平方厘米

因此，阴影区域的面积为228平方厘米。

14. AB和CD分别是两个半径分别为21厘米和7厘米的同心圆的弧，中心为O（见图12.32）。如果∠AOB = 30°，求阴影区域的面积。

解决方案

大圆扇形的面积 = (θ/360°) × πR²

= (30°/360°) × 22/7 × 21²

= 1/12 × 22/7 × 441

= 231/2 平方厘米

小圆扇形的面积 = (θ/360°) × πr²

= (30°/360°) × 22/7 × 7²

= 1/12 × 154

= 77/6 平方厘米

阴影区域面积 = 半径为R的扇形面积 - 半径为r的扇形面积

= 231/2 - 77/6

= (693 - 77)/6

= 616/6

= 308/3 平方厘米

因此，阴影区域的面积为308/3平方厘米。

15. 如图12.33所示，ABC是半径为14厘米的圆的象限，并以BC为直径画了一个半圆。求阴影区域的面积。

解决方案

象限的面积 = 1/4 × πR²

= 1/4 × 22/7 × 14²

= 154 平方厘米

△ABC的面积 = 1/2 × 底 × 高

= 1/2 × 14 × 14

= 98 平方厘米

象限的相应弓形面积 = 象限面积 - 三角形面积

= 154 - 98

= 56 平方厘米

根据ABC中的勾股定理，我们得到

BC² = AB² + AC²

BC² = 14² + 14²

BC² = 196 + 196

BC²= 392

BC = 14√2 厘米

半圆的面积 = 1/2 × πr²

= 1/2 × 22/7 × (14√2/2)²

= 154 平方厘米

阴影区域面积 = 半圆面积 - 弓形面积

= 154 - 56

= 98 平方厘米

因此，阴影区域的面积为98平方厘米。

16. 计算图12.34中两个半径均为8厘米的圆的象限之间的设计区域的面积。

解决方案

由于两个象限的半径相同。因此，它们的面积相等。

这意味着它们相应弓形的面积也相等。

△ABC的面积 = 1/2 × 底 × 高

= 1/2 × 8 × 8

= 32 平方厘米

每个象限的面积 = 1/4 × πr²

= 1/4 × 22/7 × 8²

= 352/7 平方厘米

每个弓形的面积 = 象限面积 - 三角形面积

= 352/7 - 32

= (352 - 224)/7

= 128/7 平方厘米

设计面积 = 2 × 一个弓形的面积

= 2 × 128/7

= 256/7 平方厘米

因此，设计面积为256/7平方厘米。