12 年级数学第 12 章：线性规划 的 NCERT 解决方案

练习 12.1

用图解法解决以下线性规划问题

1. 最大化 Z = 3x + 4y

约束条件为：x + y ≤ 4，x ≥ 0，y ≥ 0。

解决方案

给定 Z = 3x + 4y

约束条件：x + y ≤ 4，x ≥ 0，y ≥ 0。

求解方程 x + y ≤ 4

x + y ≤ 4，x ≥ 0，y ≥ 0

可行域的顶点为 (0, 4)、(0, 0) 和 (4, 0)。

Z 在顶点处的值

在 (0, 4) 处，

Z = 3 (0) + 4 (4) = 16

在 (4, 0) 处，

Z = 3 (4) + 4 (0) = 12

在 (0, 0) 处，

Z = 3 (0) + 4 (0) = 0

因此，Z 在 (0, 4) 处达到最大值，最大值为 16。

2. 最小化 Z = - 3x + 4y

约束条件为 x + 2y ≤ 8，3x + 2y ≤ 12，x ≥ 0，y ≥ 0

解决方案

给定 Z = -3x + 4y

约束条件：x + 2y ≤ 8，3x + 2y ≤ 12，x ≥ 0，y ≥ 0

求解方程 x + 2y ≤ 8，3x + 2y ≤ 12

x + 2y ≤ 8

可行域的顶点为 (0, 4)、(2, 3) 和 (4, 0)。

Z 在顶点处的值

在 (0, 4) 处，

Z = -3 (0) + 4 (4) = 16

在 (2, 3) 处，

Z = -3 (2) + 4 (3) = 6

在 (4, 0) 处，

Z = -3 (4) + 4 (0) = -12

因此，Z 在 (4, 0) 处达到最小值，最小值为 -12。

3. 最大化 Z = 5x + 3y

约束条件为 3x + 5y ≤ 15，5x + 2y ≤ 10，x ≥ 0，y ≥ 0。

解决方案

给定 Z = 5x + 3y

约束条件：3x + 5y ≤ 15，5x + 2y ≤ 10，x ≥ 0，y ≥ 0。

求解方程 3x + 5y ≤ 15，5x + 2y ≤ 10

3x + 5y ≤ 15

可行域的顶点为 (0, 3)、(20/19, 45/19) 和 (2, 0)。

Z 在顶点处的值

在 (0, 3) 处，

Z = 5 (0) + 3 (3) = 9

在 (20/19, 45/19) 处，

Z = 5 (20/19) + 3 (45/19)

= 100/19 + 135/19

= 235/19 = 12.36

在 (2, 0) 处，

Z = 5 (2) + 3 (0) = 10

因此，Z 在 (20/19, 45/19) 处达到最大值，最大值为 12.36。

4. 最小化 Z = 3x + 5y

约束条件为 x + 3y ≥ 3，x + y ≥ 2，x, y ≥ 0。

解决方案

给定 Z = 3x + 5y

约束条件：x + 3y ≥ 3，x + y ≥ 2，x, y ≥ 0

求解方程 x + 3y ≥ 3，x + y ≥ 2

x + 3y ≥ 3

可行域的顶点为 (0, 2)、(3/2, 1/2) 和 (3, 0)。

Z 在顶点处的值

在 (0, 2) 处，

Z = 3 (0) + 5 (2) = 10

在 (3/2, 1/2) 处，

Z = 3 (3/2) + 5 (1/2)

= 9/2 + 5/2

= 14/2 = 7

在 (3, 0) 处，

Z = 3 (3) + 5 (0) = 9

因此，Z 在 (3/2, 1/2) 处达到最小值，最小值为 7。

5. 最大化 Z = 3x + 2y

约束条件为 x + 2y ≤ 10，3x + y ≤ 15，x, y ≥ 0

解决方案

给定 Z = 3x + 2y

约束条件：x + 2y ≤ 10，3x + y ≤ 15，x, y ≥ 0

求解方程 x + 2y ≤ 10，3x + y ≤ 15

x + 2y ≤ 10

可行域的顶点为 (0, 5)、(4, 3) 和 (5, 0)。

Z 在顶点处的值

在 (0, 5) 处，

Z = 3 (0) + 2 (5) = 10

在 (4, 3) 处，

Z = 3 (4) + 2 (3)

= 12 + 6

= 18

在 (5, 0) 处，

Z = 3 (5) + 2 (0) = 15

因此，Z 在 (4, 3) 处达到最大值，最大值为 18。

6. 最小化 Z = x + 2y

约束条件为 2x + y ≥ 3，x + 2y ≥ 6，x, y ≥ 0。

解决方案

给定 Z = x + 2y

约束条件：2x + y ≥ 3，x + 2y ≥ 6，x, y ≥ 0

求解方程 2x + y ≥ 3，x + 2y ≥ 6

2x + y ≥ 3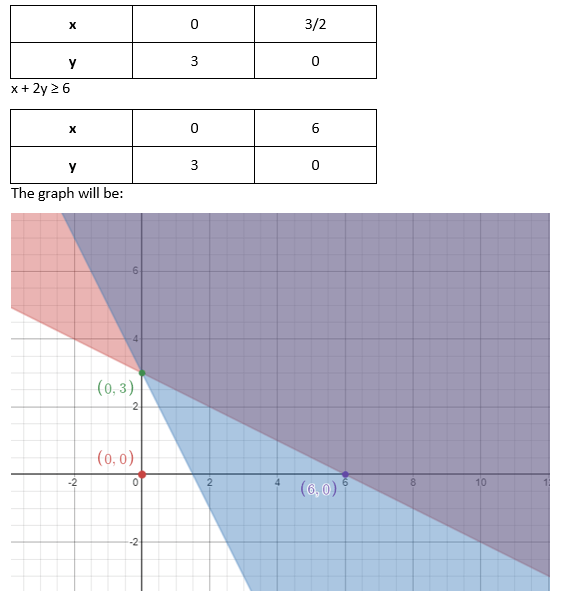

可行域的顶点为 (0, 3) 和 (6, 0)。

Z 在顶点处的值

在 (0, 3) 处，

Z = 0 + 2 (3) = 6

在 (6, 0) 处，

Z = 6 + 2 (0) = 6

现在，我们可以观察到 Z 的值在两个顶点处是相同的。取该线上的任何其他点，例如 (2, 2)，得到 Z = 2 + 2 (2) = 2 + 4 = 6。这表明 Z 的最小值发生在多于 2 个点上。

因此，Z 的值在直线 x + 2y = 6 上的每一点都最小。

证明 Z 的最小值发生在两个以上的点上。

7. 最小化和最大化 Z = 5x + 10 y 约束条件为 x + 2y ≤ 120，x + y ≥ 60，x - 2y ≥ 0，x, y ≥ 0。

解决方案

x + 2y ≤ 120

可行域将是

可行域的顶点为 (60, 30)、(120, 0)、(60, 0) 和 (40, 20)。

Z 在顶点处的值

在 (60, 30) 处，

Z = 5 (60) + 10 (30)

= 300 + 300

= 600

在 (120, 0) 处，

Z = 5 (120) + 10 (0)

= 600

在 (60, 0) 处，

Z = 5 (60) + 10 (0)

= 300

在 (40, 20) 处，

Z = 5 (40) + 10 (20)

= 200 + 200

= 400

因此，Z 在 (60, 0) 处达到最小值，最小值为 300。

Z 也以 600 的值为两个点达到最大值。

因此，Z 在连接 (60, 30) 和 (120, 0) 的所有点处都达到最大值，值为 600。

8. 最小化和最大化 Z = x + 2y

约束条件为 x + 2y ≥ 100，2x - y ≤ 0，2x + y ≤ 200; x, y ≥ 0。

解决方案

x + 2y ≥ 100

可行域将是

可行域的顶点为 (50, 100)、(20, 40)、(0, 50) 和 (0, 200)。

Z 在顶点处的值

在 (50, 100) 处，

Z = 50 + 2 (100)

= 50 + 200

= 250

在 (20, 40) 处，

Z = 20 + 2 (40)

= 20 + 80

= 100

在 (0, 50) 处，

Z = 0 + 2 (50)

= 100

在 (0, 200) 处，

Z = 0 + 2 (200)

= 400

因此，Z 在 (0, 200) 处达到最大值，最大值为 400。

Z 也以 100 的值为两个点达到最小值。

因此，Z 在连接 (20, 40) 和 (0, 50) 的所有点处都达到最小值，值为 100。

9. 最大化 Z = - x + 2y，

约束条件为：x ≥ 3，x + y ≥ 5，x + 2y ≥ 6，y ≥ 0。

解决方案

x + y ≥ 5

可行域的顶点为 (3, 2)、(4, 1) 和 (6, 0)。

Z 在顶点处的值

在 (3, 2) 处，

Z = -3 + 2 (2) = -3 + 4 = 1

在 (4, 1) 处，

Z = -4 + 2 (1)

= -2

在 (6, 0) 处，

Z = -6 + 2(0) = -6

现在，可行域是无界的，所以 Z = 1 可能或可能不是最大值。绘制不等式 -x + 2y > 1 的图形

由此产生的可行域与原始可行域有一些共同点。

因此，在给定约束条件下，Z 没有最大值。

10. 最大化 Z = x + y，

约束条件为 x - y ≤ -1，-x + y ≤ 0，x, y ≥ 0。

解决方案

x - y ≤ -1

没有公共区域，即没有可行区域。

因此，Z 没有最大值。