NCERT 10年级第6章：三角形

练习 6.1

1. 使用括号中的正确词语填空

1. 所有圆都是 _（全等的，相似的）
2. 所有正方形都是 _（相似的，全等的）
3. 所有三角形都是相似的 _（等腰的，等边的）
4. 两个边数相同的多边形相似，如果（a）它们的对应角 _ 且（b）它们的对应边 _（相等，成比例）

解决方案

1. 所有圆都是相似的。
2. 所有正方形都是相似的。
3. 所有等边三角形都是相似的。
4. 两个边数相同的多边形相似，如果（a）它们的对应角相等，并且（b）它们的对应边成比例。

2. 给出两对不同例子

1. 相似图形。
2. 不相似的图形。

解决方案

1. 一对边长不同的正方形是相似的。
   一对边长不同的等边三角形是相似的。
2. 一对角度不同的等腰三角形是不相似的。
   一对不等于90°角度的正方形和菱形是不相似的。

3. 判断下列四边形是否相似

解决方案

在四边形ABCD中，所有角都是90°。

然而，在四边形PQRS中，角度不等于90°。

因此，给定的四边形不相似。

练习 6.2

1. 在图6.17（i）和（ii）中，DE || BC。求（i）中的EC和（ii）中的AD。

解决方案

(i) 已知在∆ABC中，DE ‖ BC。因此，根据比例定理，我们有

(ii) 已知在∆ABC中，DE ‖ BC。因此，根据比例定理，我们有

2. E和F分别是∆PQR的边PQ和PR上的点。对于下列每种情况，请说明EF || QR

1. PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
2. PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
3. PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

解决方案

I. 如果比例定理得到满足，即EF || QR：

由于左侧≠右侧，因此定理不满足。

因此，EF不平行于QR。

II. 如果比例定理得到满足，即EF || QR：

由于左侧=右侧，因此定理得到满足。

因此，EF平行于QR。

III.如果比例定理得到满足，即EF || QR：

由于左侧=右侧，因此定理得到满足。

因此，EF平行于QR。

3. 在图6.18中，如果LM || CB且LN || CD，证明AM/AB = AN/AD。

解决方案

已知在∆ABC中，LM平行于CB，因此

4. 在图6.19中，DE || AC且DF || AE。证明BF/FE = BE/EC。

解决方案

5. 在图6.20中，DE || OQ且DF || OR。证明EF || QR。

解决方案

6. 在图6.21中，A、B、C分别是OP、OQ、OR边上的点，使得AB || PQ且AC || PR。证明BC || QR。

解决方案

7. 利用定理6.1，证明通过三角形一边中点作平行于另一边的直线，必平分第三边。（回忆一下，你在九年级已经证明过这个定理）。

参考：-
（定理6.1：如果一条直线平行于三角形的一条边，并与另外两条边相交于不同的点，则另外两条边被分成相同的比例。）

解决方案

设三角形为ABC，其中DE是一条通过AB边中点D并与AC边相交于点E的直线。

证明：AE = EC

证明

8. 利用定理6.2，证明连接三角形任意两边中点的直线平行于第三边。（回忆一下，你在九年级已经做过这个证明）。

参考：-
（定理6.2：如果一条直线将三角形的两条边按相同比例分割，则该直线平行于第三边。）

解决方案

设三角形为ABC，其中DE是由连接AB中点D和AC中点E形成的直线。

9. ABCD是一个梯形，其中AB || DC，对角线相交于点O。证明AO/BO = CO/DO。

解决方案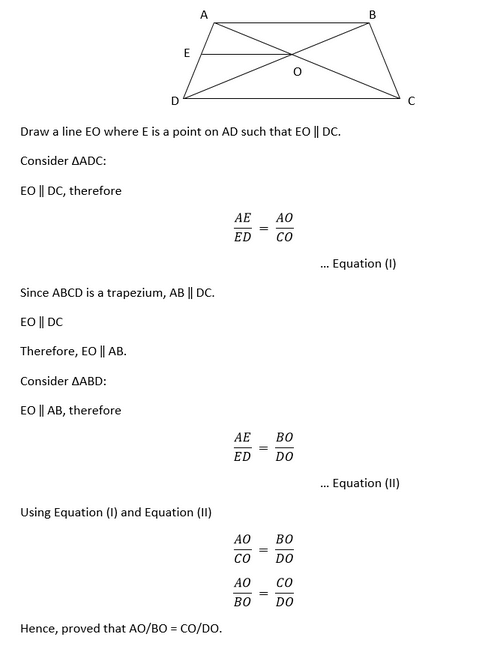

10. 梯形ABCD的对角线相交于点O，使得AO/BO = CO/DO。证明ABCD是梯形。

解决方案

因此，根据比例定理的逆定理，我们可以得出EO ‖ AB。

已知EO ‖ CD，这意味着AB ‖ CD。

由于给定的四边形有两条边平行，所以它满足成为梯形的条件。

因此，ABCD是梯形。

练习 6.3

1. 判断图6.34中的哪些三角形对是相似的。写出你用于回答问题的相似准则，并以符号形式写出相似三角形对

解决方案

(i) 在∆ABC和∆PQR中

因此，根据AAA准则，∆ABC ~ ∆PQR。

(ii) 在∆ABC和∆PQR中

因此，根据SSS准则，∆ABC ~ ∆PQR。

(iii) 在∆MPL和∆DEF中

得到的比率不相同。

因此，∆MPL不相似于∆DEF。

(iv) 在∆LMN和∆PQR中

因此，根据SAS准则，∆LMN ~ ∆PQR。

(v) 在∆ABC和∆DEF中

因此，∆ABC不相似于∆DEF。

(vi) 根据三角形的内角和性质，

因此，根据AAA准则，∆DEF ~ ∆PQR。

2. 在图6.35中，∆ODC ~ ∆OBA，∠BOC = 125°，∠CDO = 70°。求∠DOC、∠DCO和∠OAB。

解决方案

∠DOC和∠BOC构成线性对。因此

因此，∠DOC = 55°，∠DCO = 55°，∠OAB = 55°。

3. 梯形ABCD的对角线AC和BD相交于点O。利用两个三角形的相似准则，证明OA/OC = OB/OD。

解决方案

在∆AOB和∆COD中，

∠BAO = ∠OCD（内错角相等）

∠ABO = ∠ODC（内错角相等）

∠AOB = ∠COD（对顶角相等）

因此，根据AAA相似准则，∆AOB ~ ∆COD。

因为，∆AOB ~ ∆COD

因此，对应边将成比例

因此，证明了OB/OD = OA/OC。

4. 在图6.36中，QR/QS = QT/PR且∠1 = ∠2。证明∆PQS ~ ∆TQR。

解决方案

在∆PQR中，

∠PQR = ∠PRQ

因此，这是一个等腰三角形，这意味着PQ = PR。

在∆PQS和∆TQR中使用QR/QS = QT/PQ和∠Q = ∠Q，我们可以得出三角形相似（根据SAS相似准则）。

因此，证明了∆PQS ~ ∆TQR。

5. S和T分别是∆PQR的边PR和QR上的点，使得∠P = ∠RTS。证明∆RPQ ~ ∆RTS。

解决方案

在∆RPQ和∆RTS中，

∠RTS = ∠QPS（已知）

∠R = ∠R（公共角）

因此，根据AA相似准则，∆RPQ ~ ∆RTS。

6. 在图6.37中，如果∆ABE ≅ ∆ACD，证明∆ADE ~ ∆ABC。

解决方案

在∆ABE和∆ACD中

AB = AC（使用c.p.c.t.）...方程（I）

AD = AE（使用c.p.c.t.）...方程（II）

7. 在图6.38中，∆ABC的高AD和CE相交于点P。证明

1. ∆AEP ~ ∆CDP
2. ∆ABD ~ ∆CBE
3. ∆AEP ~ ∆ADB
4. ∆PDC ~ ∆BEC

解决方案

I. 在ΔAEP和ΔCDP中，

∠AEP = ∠CDP（直角）

∠APE = ∠CPD（对顶角相等）

因此，根据AA相似准则，ΔAEP ~ ΔCDP。

II. 在ΔABD和ΔCBE中，

∠ADB = ∠CEB（直角）

∠ABD = ∠CBE&（公共角）

因此，根据AA相似准则，ΔABD ~ ΔCBE。

III. 在ΔAEP和ΔABD中，

∠AEP = ∠ADB（直角）

∠PAE = ∠DAB（公共角）

因此，根据AA相似准则，ΔAEP ~ ΔABD。

IV. 在ΔPDC和ΔBEC中，

∠PDC = ∠BEC（直角）

∠PCD = ∠BCE（公共角）

因此，根据AA相似准则，ΔPDC ~ ΔBEC。

8. E是平行四边形ABCD的边AD延长线上的一点，BE与CD相交于F。证明∆ABE ~ ∆CFB。

解决方案

在∆ABE和∆CFB中，

∠BAE = ∠BCF（平行四边形的对角）

∠ABE = ∠CFB（内错角相等）

因此，根据AA相似准则，ΔABE ~ ΔCFB。

9. 在图6.39中，ABC和AMP是两个直角三角形，分别在B和M处成直角。证明

1. ∆ ABC ~ ∆AMP
2. CA/PA = BC/MP

解决方案

I. 在ΔABC和ΔAMP中，

∠ABC = ∠AMP（直角）

∠BAC = ∠MAP（公共角）

因此，根据AA相似准则，ΔABC ~ ΔAMP。

II. 由于∆ABC与∆AMP相似，它们的对应边将具有相等的比例。

故，

10. CD和GH分别是∆ABC和∆EFG的∠ACB和∠FGE的角平分线，D和H分别在∆ABC和∆EFG的边AB和FE上。如果∆ABC ~ ∆FEG，证明

1. CD/GH = AC/FG
2. ∆ DCB ~ ∆ HGE
3. ∆ DCA ~ ∆ HGF

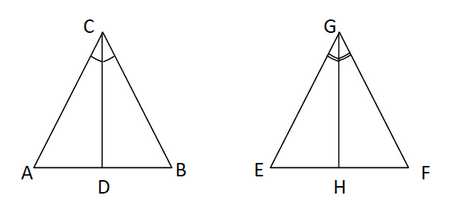解决方案

已知∆ABC ~ ∆FEG，因此

∠A = ∠F

∠B = ∠E

∠ACB = ∠FGE

两边同时除以2

∠ACB/2 = ∠FGE/2

∠ACD = ∠FGH（角平分线）

I. 现在，在∆ACD和∆FGH中

∠A = ∠F（如上所示）

∠ACD = ∠FGH（如上所示）

因此，根据AA相似准则，∆ACD ~ ∆FGH。

这意味着

II. 同样地，

∠DCB = ∠HGE

在∆DCB和∆HGE中

∠B = ∠E（如上所示）

∠DCB = ∠HGE（如上所示）

因此，根据AA相似准则，∆DCB ~ ∆HGE。

III. 在∆DCA和∆HGF中

∠A = ∠F（如上所示）

∠DCA = ∠HGF（如上所示）

因此，根据AA相似准则，∆DCA ~ ∆HGF。

11. 在图6.40中，E是等腰三角形ABC的边CB延长线上的一点，其中AB = AC。如果AD ⊥ BC且EF ⊥ AC，证明∆ABD ~ ∆ECF。

解决方案

在等腰三角形中，相等边的对角也相等。因此，

∠ABD = ∠ACD = ∠ECF

在∆ ABD和∆ ECF中

∠ADB = ∠EFC（直角）

∠ABD = ∠ECF（如上所示）

因此，根据AA相似准则，∆ ABD ~ ∆ ECF。

12. 三角形ABC的边AB和BC以及中线AD分别与△PQR的边PQ和QR以及中线PM成比例（见图6.41）。证明∆ ABC ~ ∆PQR。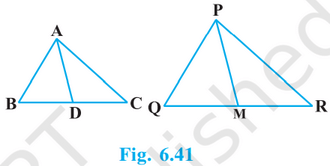

解决方案

已知

因此，根据SSS相似准则，∆ABD ~ ∆PQM。

这意味着

∠ABD = ∠PQM（相似三角形的对应角）

∠ABC = ∠PQR

在∆ABC和∆PQR中

AB/PQ = BC/QR（已知）

∠ABC = ∠PQR（如上所示）

因此，根据SAS相似准则，∆ABC ~ ∆PQR。

13. D是三角形ABC的边BC上的一点，使得∠ADC = ∠BAC。证明CA² = CB.CD。

解决方案

在∆ADC和∆BAC中

∠ADC = ∠BAC（已知）

∠ACD = ∠BCA（公共角）

因此，根据AA相似准则，∆ADC ~ ∆BAC。

这意味着

CA/CB = CD/CA（相似三角形的对应边）

CA² = CB.CD

14. 三角形ABC的边AB和AC以及中线AD分别与另一个三角形PQR的边PQ和PR以及中线PM成比例。证明∆ABC ~ ∆PQR。

解决方案

首先，我们将AD和PM线延长到外部点E和N，使得AD = DE且PM = MN，然后分别连接E和N与C和R。

在∆ABD和∆CDE中

. ∠ADB = ∠CDE（对顶角相等）

AD = DE（通过构造）

BD = DC（D是BC的中点）

因此，根据SAS全等准则，∆ABD ≅ ∆CDE。

这意味着

AB = CE（通过c.p.c.t.）

在∆PQM和∆MNR中

. ∠PMQ = ∠NMR（对顶角相等）

PM = MN（通过构造）

QR = MR（M是QR的中点）

因此，根据SAS全等准则，∆PMQ ≅ ∆NMR。

这意味着

PQ = RN（通过c.p.c.t.）

已知

因此，根据SSS相似准则，∆ACE ~ ∆PRN。

这意味着

∠CAE = ∠RPN（相似三角形的对应角）

∠CAD = ∠RPM

同样地，∠BAD = ∠QPM。

将以上两个方程相加

∠CAD + ∠BAD = ∠RPM + ∠QPM

∠BAC = ∠QPR

在∆ABC和∆PQR中

∠BAC = ∠QPR（如上所示）

AB/PQ = AC/PR（已知）

因此，根据SAS相似准则，∆ABC ~ ∆PQR。

15. 一根长6米的垂直杆子在地面上投下4米长的影子，同时，一座塔投下28米长的影子。求塔的高度。

解决方案

设AB为杆子，其影子为BC，设塔为PQ，影子为QR。

如果我们连接杆子和塔的顶部到它们各自影子的末端，我们可以得到三角形ABC和PQR。

由于影子BC和QR在同一时间被投射，太阳的高度角将相同。

因此，

∠ACB = ∠PRQ

在∆ABC和∆PQR中

∠ACB = ∠PRQ（如上所示）

∠ABC = ∠PQR（直角）

因此，根据AA相似准则，∆ABC ~ ∆PQR。

这意味着

AB/PQ = BC/QR（相似三角形的对应边）

AB = 6 m, BC = 4 m

QR = 28 m

6/PQ = 4/28

6/PQ = 1/7

PQ = 42 m

因此，塔的高度为42米。

16. 如果AD和PM分别是三角形ABC和PQR的中线，其中∆ ABC ~ ∆PQR，证明AB/PQ = AD/PM。

解决方案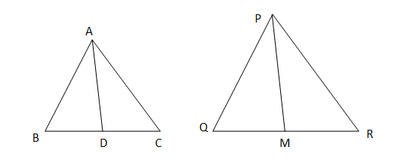

已知∆ ABC ~ ∆PQR，这意味着

∠ABC = ∠PQR（相似三角形的对应角）

∠ABD = ∠PQM

在∆ABD和∆PQM中

AB/PQ = BD/QM（如上所示）

∠ABD = ∠PQM（如上所示）

因此，根据SAS相似准则，∆ABD ~ ∆PQM。

这意味着

AB/PQ = AD/PM（相似三角形的对应边）

因此，证明了AB/PQ = AD/PM。

练习6.4

1. 设∆ ABC ~ ∆ DEF，它们的面积分别为64 cm²和121 cm²。如果EF = 15.4 cm，求BC。

解决方案

因为∆ ABC ~ ∆ DEF，所以

因此，BC = 11.2 cm²。

2. 梯形ABCD的对角线AB || DC相交于点O。如果AB = 2 CD，求三角形AOB和COD的面积之比。

解决方案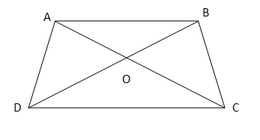

在∆AOB和∆COD中

∠AOB = ∠COD（对顶角相等）

∠ABO = ∠CDO（内错角相等）

因此，根据AA相似准则，∆AOB ~ ∆COD。

这意味着

因此，三角形AOB和COD的面积之比为4:1。

3. 在图6.44中，ABC和DBC是两个以BC为公共底的三角形。如果AD与BC相交于O，证明ar(ABC)/ar(DBC) = AO/DO。

解决方案

我们需要作两条线段AP和DM，其中P和M是BC上的点，使得AP和DM都垂直于BC。

三角形面积 = ½ × 底 × 高

∆ABC的面积 = ½ × BC × AP

∆DBC的面积 = ½ × BC × DM

∆ABC和∆DBC面积之比 = (½ × BC × AP) / (½ × BC × DM)

ar (∆ABC)/ ar (∆DBC) = AP/DM ... 方程（I）

在∆AOP和∆DOM中

∠AOP = ∠DOM（对顶角相等）

∠APO = ∠DMO&（直角）

因此，根据AA相似准则，∆AOP ~ ∆DOM。

这意味着

AO/DO = PA/MD（相似三角形的对应边）

AO/DO = AP/DM ... 方程（II）

从方程（I）和方程（II）得出，

ar (∆ABC)/ ar (∆DBC) = AO/DO

4. 如果两个相似三角形的面积相等，证明它们是全等的。

解决方案

设有两个相似三角形ABC和PQR，其中Area of ABC = Area of PQR。

AB/PQ = 1

AB = PQ

类似地，

BC = QR

AC = PR

因此，根据SSS全等准则，∆ABC ≅ ∆PQR。

因此，证明了两个面积相等的相似三角形是全等的。

5. D、E和F分别是∆ ABC的边AB、BC和CA的中点。求∆ DEF和∆ ABC的面积之比。

解决方案

由于D和F分别是边AB和AC的中点，因此，根据中点定理

DF ‖ BC。

在∆ABC和∆ADF中

∠BAC = ∠DAF（公共角）

∠ABC = ∠ADF（对应角）

因此，根据AA相似准则，∆ABC ~ ∆ADF。

这意味着

从上述方程，我们可以得出

Ar (∆ADF) = ¼ (Ar (∆ABC))

Ar (∆BED) = ¼ (Ar (∆ABC))

Ar (∆CEF) = ¼ (Ar (∆ABC))

现在，

因此，三角形DEF和ABC的面积之比为1:4。

6. 证明两个相似三角形的面积之比等于其对应中线长度之比的平方。

解决方案

设有两个相似三角形ABC和PQR，其中AD和PM分别是三角形的中线。

证明：ar (∆ABC)/ ar (∆PQR) = AD²/ PM²

证明

已知∆ABC ~ ∆PQR，这意味着

∠ABC = ∠PQR（相似三角形的对应角）

∠ABD = ∠PQM

现在，在∆ABD和∆PQM中

∠ABD = ∠PQM（如上所示）

AB/PQ = BD/QM（如上所示）

因此，根据SAS相似准则，∆ABD ~ ∆PQM。

这意味着

因此，证明了两个相似三角形的面积之比等于其对应中线长度之比的平方。

7. 证明在一个正方形的一条边上构造的等边三角形的面积等于在其对角线上构造的等边三角形面积的一半。

解决方案

设有一个正方形ABCD，在其一条边和一条对角线上分别构造了等边三角形ABD和ACE。

证明：ar (∆ABD) = ½ (ar (∆ACE))

证明

根据勾股定理在ABC中，我们得到

AC² = AB² + BC²

AB = BC，因为ABCD是正方形

AC² = 2AB² ... 方程（I）

已知ABD和ACE都是等边三角形。

因此，根据AAA相似准则，∆ABD ~ ∆ACE。

这意味着

因此，证明了在一个正方形的一条边上构造的等边三角形的面积等于在其对角线上构造的等边三角形面积的一半。

选择正确的答案并说明理由

8. ABC和BDE是两个等边三角形，其中D是BC的中点。三角形ABC和BDE的面积之比是

(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4

解决方案

D是BC的中点，因此

BD = DC = ½(BC) ... 方程（I）

AB = BC（等边三角形的边）... 方程（II）

由于∆ABC和∆BDE都是等边三角形，因此

根据AA相似准则，∆ABC ~ ∆BDE。

这意味着

因此，正确答案是(C) 4 : 1。

9. 两个相似三角形的边长之比为4:9。这些三角形的面积之比是

(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81

解决方案

设有两个相似三角形ABC和DEF。

那么，根据题目

由于已知三角形ABC和DEF相似。因此，

因此，正确答案是(D) 16 : 81。

练习6.5

1. 下面给出了三角形的边长。判断哪些是直角三角形。如果是直角三角形，写出其斜边的长度。

1. 7 cm, 24 cm, 25 cm
2. 3 cm, 8 cm, 6 cm
3. 50 cm, 80 cm, 100 cm
4. 13 cm, 12 cm, 5 cm

解决方案

I. 较小两边长度的平方和 = 7² + 24² = 49 + 576 = 625 cm²

最长边长度的平方 = 25² = 625 cm²

因此，该三角形满足勾股定理，是直角三角形。

该三角形的斜边长度为25厘米。

II. 较小两边长度的平方和 = 3² + 6² = 9 + 36 = 45 cm²

最长边长度的平方 = 8² = 64 cm²

因此，该三角形不满足勾股定理，不是直角三角形。

III. 较小两边长度的平方和 = 50² + 80² = 2500 + 6400 = 8900 cm²

最长边长度的平方 = 100² = 10000 cm²

因此，该三角形不满足勾股定理，不是直角三角形。

IV. 较小两边长度的平方和 = 5² + 12² = 25 + 144 = 169 cm²

最长边长度的平方 = 13² = 169 cm²

因此，该三角形满足勾股定理，是直角三角形。

该三角形的斜边长度为13厘米。

2. PQR是直角三角形，直角在P处，M是QR上的一点，使得PM ⊥ QR。证明PM² = QM . MR。

解决方案

根据∆PQM中的勾股定理，我们得到

PQ² = PM² + QM²

PM² = PQ² - QM² ... 方程（I）

根据∆PRM中的勾股定理，我们得到

PR² = PM² + MR²

PM² = PR² - MR² ... 方程（II）

将方程（I）和方程（II）相加

2PM² = PQ² - QM² + PR² - MR²

2PM² = (PQ² + PR²) - (QM² + MR²)

2PM² = (QR²) - (QM² + MR²) [根据勾股定理，PQ² + PR² = QR²]

2PM² = QR² - QM² - MR²

2PM² = (QM + MR)² - QM² - MR² [QR = QM + MR]

2PM² = QM² + MR² + 2QM.MR - QM² - MR²

2PM² = 2QM.MR

PM² = QM.MR

因此，证明了PM²

3. 在图6.53中，ABD是直角三角形，直角在A处，AC ⊥ BD。证明

1. AB² = BC . BD
2. AC² = BC . DC
3. AD² = BD . CD

解决方案

I. 在∆ABD和∆CBA中

∠BAD = ∠BCA（直角）

∠ABD = ∠ABC（公共角）

因此，根据AA相似准则，∆ABD ~ ∆CBA。

这意味着

AB/CB = BD/AB（相似三角形的对应边）

AB² = BC.BD

II. 因为我们已经证明了∆ABD ~ ∆CBA，所以

∠CAB = ∠BDA（相似三角形的对应角）

∠CAB = ∠CDA

在∆CBA和∆CAD中

∠ACB = ∠ACD（直角）

∠CAB = ∠CDA（如上所示）

因此，根据AA相似准则，∆CBA ~ ∆CAD。

这意味着

AC/BC = DC/AC（相似三角形的对应边）

AC² = BC.DC

III. 在∆DCA和∆DAB中

∠DCA = ∠DAB（直角）

∠CDA = ∠ADB（公共角）

因此，根据AA相似准则，∆DCA ~ ∆DAB。

这意味着

CD/AD = AD/BD（相似三角形的对应边）

AD² = BD.CD

4. ABC是直角三角形，直角在C处。证明AB² = 2AC² 。

解决方案

已知∆ABC是等腰三角形。这意味着相等角的对边相等。

由于∠ACB已知为直角。因此，∠ABC和∠BAC是相等角，边AC = BC。

根据ABC中的勾股定理，我们得到

AB² = AC² + BC²

AB² = AC² + AC²

AB² = 2AC²

因此，证明了AB² = 2AC²。

5. ABC是等腰三角形，AC = BC。如果AB² = 2 AC²，证明ABC是直角三角形。

解决方案

已知

AB² = 2AC²

AB² = AC² + AC²

AB² = AC² + BC²（因为已知AC = BC）

上述方程满足勾股定理。

因此，∆ABC是直角三角形。

6. ABC是边长为2a的等边三角形。求其各边高。

解决方案

让我们在三角形ABC中画出高AD。

在∆ADB和∆ADC中

∠ADB = ∠ADC（直角）

AD = AD（公共边）

AB = AC（等边三角形ABC的边）

因此，根据RHS全等准则，∆ADB ≅ ∆ADC。

这意味着

BD = CD（通过c.p.c.t.）

因此，

BC = 2BD

BD = BC/2

BD = a

根据∆ADB中的勾股定理，我们得到

AB² = BD² + AD²

AD² = AB² - BD²

AD² = 4a² - a²

AD² = 3a²

AD = √3a

因此，三角形ABC的每条高线的长度为√3a。

7. 证明菱形的各边平方和等于其对角线平方和。

解决方案

设菱形为ABCD，其对角线在O点互相平分。

证明：AB² + BC² + CD² + AD² = AC² + BD²

证明

我们知道菱形的对角线互相平分且互相垂直。因此，AOB、AOD、BOC、COD都是直角三角形。

这也意味着AO = CO且BO = DO，因为O是平分点。

根据∆AOB中的勾股定理，我们得到

AB² = AO² + BO²

类似地，

BC² = BO² + CO²

CD² = CO² + DO²

AD² = AO² + DO²

将以上所有方程相加，我们得到

AB² + BC² + CD² + AD² = AO² + BO² + BO² + CO² + CO² + DO² + AO² + DO²

AB² + BC² + CD² + AD² = 2(AO² + BO² + CO² + DO²)

AB² + BC² + CD² + AD² = 2(AO² + CO² + BO² + DO²)

由于AO = CO且BO = DO。因此，

AB² + BC² + CD² + AD² = 2(2AO² + 2BO²)

AB² + BC² + CD² + AD² = 4AO² + 4BO²

AB² + BC² + CD² + AD² = (2AO)² + (2BO)²

O是AC和BD的中点，所以2AO = AC且2BO = BD。因此，

AB² + BC² + CD² + AD² = AC² + BD²

因此，证明了菱形的各边平方和等于其对角线平方和。

8. 在图6.54中，O是三角形ABC内部的一点，OD ⊥ BC，OE ⊥ AC且OF ⊥ AB。证明

1. OA² + OB² + OC² - OD² - OE² - OF² = AF² + BD² + CE²，
2. AF² + BD² + CE² = AE² + CD² + BF²。

解决方案

让我们连接OB、OA和OC。

I. 根据∆AOF中的勾股定理，我们得到

OA² = AF² + OF²

根据∆BOD中的勾股定理，我们得到

OB² = OD² + BD²

根据∆COE中的勾股定理，我们得到

OC² = OE² + EC²

将上述方程相加，我们得到

OA² + OB² + OC² = AF² + OF² + OD² + BD² + OE² + EC²

OA² + OB² + OC² - OD² - OE² - OF² = AF² + BD² + EC²

因此，证明完毕。

II. OA² + OB² + OC² - OD² - OE² - OF² = AF² + BD² + EC²

(OA² - OE²) + (OC² - OD²) + (OB² - OF²) = AF² + BD² + EC²

根据∆AOE中的勾股定理，我们得到

OA² = OE² + AE²

OA² - OE² = AE²

类似地，

OC² - OD² = CD²

OB² - OF² = BF²

故，

(OA² - OE²) + (OC² - OD²) + (OB² - OF²) = AF² + BD² + EC²

AE² + CD² + BF² = AF² + BD² + EC²

9. 一根10米长的梯子够到了8米高的窗户。求梯脚与墙基的距离。

解决方案

设AB为梯子，其到达A点的窗户，墙基在C点。

墙体将垂直于地面，因此ABC将形成一个直角三角形，其直角在C处。

AB = 10 m, AC = 8 m

根据ABC中的勾股定理，我们得到

AB² = AC² + BC²

10² = 8² + BC²

100 = 64 + BC²

36 = BC²

BC = 6 m

因此，梯脚与墙基之间的距离为6米。

10. 一根连接垂直杆子（高18米）的拉线长24米，另一端附有桩。为了使拉线绷紧，桩应打在离杆子底部多远的地方？

解决方案

设线为AB，杆子为AC。BC为桩与杆子底部的距离。

∆ACB是直角三角形，直角在C处。

根据ABC中的勾股定理，我们得到

AB² = AC² + BC²

24² = 18² + BC²

576 - 324 = BC²

252 = BC²

BC = 6√7 m

因此，为了使拉线绷紧，桩应打在离杆子底部6√7米的地方。

11. 一架飞机从机场起飞，以每小时1000公里的速度向正北方向飞行。同时，另一架飞机从同一机场起飞，以每小时1200公里的速度向正西方向飞行。1.5小时后，两架飞机相距多远？

解决方案

设A为向北飞行的飞机当前位置，B为向西飞行的飞机当前位置。设O为两架飞机的起点。

AOB将构成一个直角三角形，直角在O处。

向北飞行的飞机的速度 = 1000公里/小时

= 1200 × 3/2 = 1800公里

根据AOB中的勾股定理，我们得到

AB² = AO² + BO²

AB² = 1500² + 1800²

AB² = 2250000 + 3240000

AB² = 5490000

AB = 300√61公里

12. 两根高度分别为6米和11米的杆子立在平地上。如果两杆底部之间的距离为12米，求两杆顶端之间的距离。

解决方案

设AB为较高的杆子，CD为较短的杆子。它们顶端之间的距离是AC，底部之间的距离是BD。我们将从C画一条虚线到O，O是杆子AB上的一点，使得OC ‖ BD。

杆子垂直于地面，所以∠BDC是直角。

∠AOC = ∠BDC（对应角）

因此，∆AOC是直角三角形。

OCBD构成一个矩形，因为OC ‖ BD且AB ‖ CD。

这意味着

OC = BD = 12 m

OB = CD = 6 m

现在，AB = AO + OB

AO = AB - OB = 11 - 6 = 5 m

根据AOC中的勾股定理，我们得到

AC² = AO² + OC²

AC² = 5² + 12²

AC² = 25 + 144

AC² = 169

AC = 13 m

因此，两杆顶端之间的距离为13米。

13. D和E分别是三角形ABC的边CA和CB上的点，直角在C处。证明AE² + BD² = AB² + DE²。

根据ABC中的勾股定理，我们得到

AB² = AC² + BC² ... 方程（I）

根据AEC中的勾股定理，我们得到

AE² = AC² + EC²

根据BDC中的勾股定理，我们得到

BD² = BC² + DC²

根据DEC中的勾股定理，我们得到

DE² = DC² + EC² ... 方程（II）

因此，

AE² + BD² = AC² + EC² + BC² + DC²

AE² + BD² = (AC² + BC²) + (EC² + DC²)

从方程（I）和方程（II）得出

AE² + BD² = AB² + DE²

因此，证明完毕。

14. ABC是三角形的一条边BC上的点D，使得DB = 3 CD（见图6.55）。证明2 AB² = 2 AC² + BC²。

解决方案

BC = BD + CD

BC = 3CD + CD

BC/4 = CD

根据ADB中的勾股定理，我们得到

AB² = AD² + BD² ... 方程（I）

根据ADC中的勾股定理，我们得到

AC² = AD² + CD² ... 方程（II）

将方程（II）从方程（I）中减去

AB² - AC² = BD² - CD²

AB² - AC² = (3CD)² - CD²

AB² - AC² = 9CD² - CD²

AB² - AC² = 8CD²

AB² - AC² = 8(BC/4)²

AB² - AC² = BC²/2

2(AB² - AC²) = BC²

2AB² - 2AC² = BC²

2AB² = 2AC² + BC²

因此，证明完毕。

15. 在等边三角形ABC中，D是边BC上的一点，使得BD = 1/3 BC。证明9 AD² = 7 AB²。

解决方案

让我们在∆ABC中画出高AE。

由于AE是等边三角形的高，因此它也充当了中线。

BE = CE = BC/2

根据ABE中的勾股定理，我们得到

AB² = BE² + AE²

AE² = AB² - BE²

AE² = AB² - BC²/4

根据ADE中的勾股定理，我们得到

AD² = AE² + DE²

AD² = AE² + (BE - BD)²

AD² = AB² - BC²/4 + (BC/2 - BC/3)²

AD² = AB² - BC²/4 + (BC/6)²

AD² = AB² - BC²/4 + BC²/36

AD² = AB² - 8BC²/36

AD² = AB² - 2BC²/9

AD² = (9AB² - 2BC²)/9

9AD² = 9AB² - 2AB² （BC = AB，因为ABC是等边三角形）

9AD² = 7AB²

因此，证明完毕。

16. 在一个等边三角形中，证明其一条边平方的三倍等于其一条高平方的四倍。

解决方案

设有一个等边三角形ABC，高为AD，每条边长为a。

证明：3a² = 4AD²

证明

我们知道等边三角形的高也充当了中线。因此，

BD = CD = BC/2

根据ABD中的勾股定理，我们得到

AB² = AD² + BD²

AB² = AD² + BC²/4

a² = AD² + a²/4

3a²/4 = AD²

3a² = 4AD²

因此，证明了边平方的三倍等于高平方的四倍。

17. 选择正确的答案并说明理由：在∆ABC中，AB = 6√3 cm，AC = 12 cm，BC = 6 cm。角B是

(A) 120° (B) 60° (C) 90° (D) 45°

解决方案

AB² = (6√3)² = 108

AC² = 12² = 144

BC² = 6² = 36

可以看出，AB² + BC² = 144 = AC²。

这意味着该三角形满足勾股定理，AC是斜边。因此，角B是90°。

因此，正确选项是(C) 90°。

练习6.6（选做）

1. 在图6.56中，PS是∆PQR的∠QPR的角平分线。证明QS/SR = PQ/PR。

解决方案

让我们将QP线延长到一个外部点T，使得TR平行于PS。

∠QPS = ∠SPR，因为PS是∠QPR的角平分线。

∠QPS = ∠QTR（对应角）

∠SPR = ∠PRT（内错角相等）

因此，∠PRT = ∠QTR。

我们知道，如果三角形的两个角相等，则该三角形是等腰三角形，并且相等角的对边也相等。因此，

PT = PR

根据QRT中的比例定理，我们得到

QS/SR = PQ/PT

QS/SR = PQ/PR

因此，证明完毕。

2. 在图6.57中，D是∆ABC的斜边AC上的一点，使得BD ⊥ AC，DM ⊥ BC且DN ⊥ AB。证明

1. DM² = DN . MC
2. DN² = DM . AN

解决方案

从图中可以得出，DBMN是一个矩形，因为它的对边平行且每个角都是90°。

这意味着

DN = BM且DM = BN。

(i). ∠CDM = ∠CDB - ∠BDM

∠CDM = 90° - ∠BDM

∠CDM + ∠BDM = 90°

同样，在∆CDM中

∠CDM + ∠CMD + ∠MCD = 180°

∠CDM + 90° + ∠MCD = 180°

∠CDM + ∠MCD = 90°

因此，我们可以说

∠CDM + ∠MCD = ∠CDM + ∠BDM（两边都等于90°）

∠MCD = ∠BDM

在∆CDM和∆MDB中

∠MCD = ∠BDM（如上所示）

∠CMD = ∠BMD（直角）

因此，根据AA相似准则，∆CDM ~ ∆MDB。

这意味着

DM/BM = MC/DM

DM² = MC.BM

我们已经证明了BM = DN。

DM² = DN.MC

(ii). ∠ADB = ∠ADN + ∠BDN

∠ADN + ∠BDN = 90°

同样，在∆ADN中

∠AND + ∠ADN + ∠DAN = 180°

90° + ∠ADN + ∠DAN = 180°

∠ADN + ∠DAN = 90°

因此，我们可以说

∠ADN + ∠DAN = ∠ADN + ∠BDN（两边都等于90°）

∠DAN = ∠BDN

在∆ADN和∆NDB中

∠DAN = ∠BDN（如上所示）

∠CMD = ∠BMD（直角）

因此，根据AA相似准则，∆ADN ~ ∆NDB。

这意味着

DN/BN = NA/DN

DN² = AN.BN

我们已经证明了BN = DM。

DN² = DM.AN

因此，证明完毕。

3. 在图6.58中，ABC是一个三角形，其中∠ABC > 90°且AD ⊥ CB延长线。证明AC² = AB² + BC² + 2 BC . BD。

解决方案

根据ABD中的勾股定理，我们得到

AB² = AD² + BD²

根据ACD中的勾股定理，我们得到

AC² = AD² + CD²

AC² = AD² + (BD + BC)²

AC² = AD² + BD² + BC² + 2 BC.BD

我们已经知道AD² + BD² = AB²，因此

AC² = AB² + BC² + 2 BC.BD

因此，证明完毕。

4. 在图6.59中，ABC是一个三角形，其中∠ ABC < 90°且AD ⊥ BC。证明AC² = AB² + BC² - 2 BC . BD。

解决方案

根据ABD中的勾股定理，我们得到

AB² = AD² + BD²

根据ACD中的勾股定理，我们得到

AC² = AD² + CD²

AC² = AD² + (BC - BD)²

AC² = AD² + BD² + BC² - 2 BC.BD

我们已经知道AD² + BD² = AB²，因此

AC² = AB² + BC² - 2 BC.BD

因此，证明完毕。

5. 在图6.60中，AD是三角形ABC的中线，AM ⊥ BC。证明

1. AC² = AD² + BC . DM + (BC/2)²
2. AB² = AD² - BC . DM + (BC/2)²
3. AC² + AB² = 2 AD² + BC²/2

解决方案

已知AD是三角形ABC的中线，因此

BD = CD = BC/2 ... 方程（I）

根据AMD中的勾股定理，我们得到

AD² = AM² + DM²

(i). 根据ACM中的勾股定理，我们得到

AC² = AM² + CM²

AC² = AM² + (CD + DM)²

AC² = AM² + DM² + CD² + 2 CD.DM

使用方程（I）

AC² = AM² +DM² + (BC/2)² + 2(BC/2)DM

我们已经知道AM² + DM² = AD²，因此

AC² = AD² + (BC/2)² + 2(BC/2)DM

AC² = AD² + BC .DM + (BC/2)²

(ii). 根据ABM中的勾股定理，我们得到

AB² = AM² + BM²

我们知道AD² = AM² + DM²

AM² = AD² - DM²

现在，

AB² = AD² - DM² + BM²

AB² = AD² - DM² + (BD - DM)²

AB² = AD² - DM² + BD² + DM² - 2BD.DM

使用方程（I）

AB² = AD² + (BC/2)² - 2 (BC/2).DM

AB² = AD² + (BC/2)² - BC .DM

(iii). 根据ABM中的勾股定理，我们得到

AB² = AM² + BM²

根据AMC中的勾股定理，我们得到

AC² = AM² + MC²

将上述两个方程相加，我们得到

AB² + AC² = 2AM² + BM² + MC²

AB² + AC² = 2AM² + (BD - DM)² + (DM + CD)²

AB² + AC² = 2AM² + BD² + DM² - 2 BD.DM + DM² + CD² + 2 DM.CD

AB² + AC² = 2AM² + 2DM² + BD² + CD² + 2DM(CD - BD)

AB² + AC² = 2(AM² + DM²) + BD² + CD² + 2DM(CD - BD)

我们知道AM² + DM² = AD²，因此

AB² + AC² = 2AD² + BD² + CD² + 2DM(CD - BD)

使用方程（I）

AB² + AC² = 2AD² + (BC/2)² + (BC/2)² + 2DM(BC/2 - BC/2)

AB² + AC² = 2AD² + BC²/4 + BC²/4

AB² + AC² = 2AD² + BC²/2

因此，证明完毕。

6. 证明平行四边形对角线平方和等于其边平方和。

解决方案

设ABCD为平行四边形，AB ‖ CD且高为AE。我们将BA延长到一点F，使得DF ? BF。

证明：AC² + BD² = AB² + BC² + CD² + AD²

证明

根据ADF中的勾股定理，我们得到

AD² = AF² + DF²

根据BDF中的勾股定理，我们得到

BD² = BF² + DF²

BD² = (AB + AF)² + DF²

BD² = AB² + AF² + 2 AB.AF + DF²

我们知道AF² + DF² = AD²，因此

BD² = AB² + AD² + 2 AB.AF; ... 方程（I）

根据ADE中的勾股定理，我们得到

AD² = AE² + DE²

根据ACE中的勾股定理，我们得到

AC² = AE² + CE²

AC² = AE² + (CD - DE)²

AC² = AE² + CD² - 2 CD.DE + DE²

我们知道AE² + DE² = AD²，因此

AC² = AD² + CD² - 2 CD.DE ... 方程（II）

将方程（I）和方程（II）相加

AC² + BD² = AD² + CD² - 2 CD.DE + AB² + AD² + 2 AB.AF

因为ABCD是平行四边形，所以

AB = CD且BC = AD（平行四边形的对边）

另外，可以看出AEDF构成一个矩形，这意味着

AF = DE；（矩形的对边）

因此，

AC² + BD² = AD² + CD² + AB² + BC² + 2 AB.AF - 2 AB.AF

AC² + BD² = AD² + CD² + AB² + BC²

因此，证明了平行四边形对角线平方和等于其边平方和。

7. 在图6.61中，两条弦AB和CD在点P处相交。证明

1. ∆ APC ~ ∆ DPB
2. AP . PB = CP . DP

解决方案

AP = BP = CP = DP，因为它们是给定圆的半径。

因此，AP/DP = 1 = CP/BP。

(i). 在∆APC和∆DPB中

AP/DP = CP/BP（如上所示）

∠APC = ∠DPB（对顶角相等）

因此，根据SAS相似准则，∆APC ~ ∆DPB。

(ii). 我们已经证明了AP/DP = CP/BP。这意味着

AP.BP = CP.DP

AP.PB = PC.DP

因此，证明完毕。

8. 在图6.62中，圆的两条弦AB和CD在点P处相交（当延长时）在圆外。证明

1. ∆ PAC ~ ∆ PDB
2. PA . PB = PC . PD

解决方案

(i). 由于ABCD是一个包含在圆中的四边形，因此ABCD构成一个圆内接四边形。这意味着，

∠PAC = ∠BDC（圆内接四边形的外角等于

相对的内角）

在∆PAC和∆PDB中

∠PAC = ∠BDC（如上所示）

∠APC = ∠BPD（公共角）

因此，根据AA相似准则，∆PAC ~ ∆PDB。

(ii). 我们已经证明了∆PAC ~ ∆PDB。

这意味着

AP/DP = PC/PB（相似三角形的对应边）

AP.PB = PC.DP

因此，证明完毕。

9. 在图6.63中，D是∆ ABC的边BC上的一点，使得BD/CD = AB/AC。证明AD是∠BAC的角平分线。

解决方案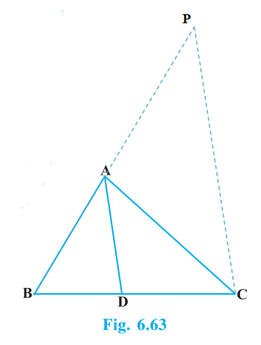

让我们将BA延长到一个外部点P，使得AP = AC。

BC/ CD = AB/ AC（已知）

BC/CD = AB/AP（AP = AC）

因此，根据比例定理的逆定理，我们可以说AD ‖ CP。

∠BAD = ∠APC（对应角）

∠CAD = ∠ACP（内错角相等）

∆ACP是一个等腰三角形，因为AP = AC。这意味着

∠APC = ∠ACP（等腰三角形中相等边的对角）

因此，

∠BAD = ∠CAD

AD将∠BAC分成两个相等的角。

因此，AD是∠BAC的角平分线。

10. Nazima正在溪流中钓鱼。她的钓鱼竿尖在水面以上1.8米，绳子末端的鱼饵落在水面上，距离杆尖正下方3.6米，距离杆尖2.4米。假设她的绳子（从竿尖到鱼饵）是绷紧的，她有多少绳子露在外面（见图6.64）？如果她以每秒5厘米的速度收线，12秒后鱼会离她多远？

解决方案

这种情况可以用一个三角形ABC来表示，其中A是钓鱼竿的尖端，C是绳子的末端，BC是水面。

根据ABC中的勾股定理，我们得到

AC² = AB² + BC²

AC² = (1.8)² + (2.4)²

AC² = 3.24 + 5.76

AC² = 9

AC = 3

因此，Nazima的钓鱼竿绳子露在外面3米。

已知她以每秒5厘米的速度收线。因此，

Nazima在1秒内收的绳子长度 = 5厘米

Nazima在12秒内收的绳子长度 = 12 × 5 = 60厘米 = 0.6米

设鱼的新位置为D，它是水面BC上的一个点。

12秒后剩余的绳子长度 = AD = 3 - 0.6米 = 2.4米

根据ABD中的勾股定理，我们得到

AD² = AB² + BD²

(2.4)² = (1.8)² + BD²

BD² = (2.4)² - (1.8)²

BD² = 5.76 - 3.24

BD² = 2.52

BD = 1.59米（近似值）

鱼的水平距离 = 1.2 + BD = 1.2 + 1.59 = 2.79米

因此，鱼离Nazima的水平距离约为2.79米。