NCERT 解决方案 六年级数学

第三章：数字游戏

练习3.1

1. 写出下列各数的因数

(a) 24

答案 1, 2, 3, 4, 6, 8, 12, 24

1 × 24 = 24

2 × 12 = 24

3 × 8 = 24

6 × 4 = 24

或

24 × 1 = 24

12 × 2 = 24

8 × 3 = 24

4 × 6 = 24

(b) 15

答案 1, 3, 5, 15

1 × 15 = 15

3 × 5 = 15

或

15 × 1 = 15

5 × 3 = 15

(c) 21

答案 1, 3, 7, 21

1 × 21 = 21

3 × 7 = 21

或

21 × 1 = 21

7 × 3 = 21

(d) 27

答案 1, 3, 9, 27

1 × 27 = 27

3 × 9 = 27

或

27 × 1 = 27

9 × 3 = 27

(e) 12

答案 1, 2, 3, 4, 6, 12

1 × 12 = 12

2 × 6 = 12

3 × 4 = 12

或

12 × 1 = 12

6 × 2 = 12

4 × 3 = 12

(f) 20

答案 1, 2, 4, 5, 10, 20

1 × 20 = 20

2 × 10 = 20

5 × 4 = 20

或

20 × 1 = 20

10 × 2 = 20

4 × 5 = 20

(g) 18

答案 1, 2, 3, 6, 9, 18

1 × 18 = 18

2 × 9 = 18

3 × 6 = 18

或

18 × 1 = 18

9 × 2 = 18

6 × 3 = 18

(h) 23

答案 1, 23

1 × 23 = 23

或

23 × 1 = 23

(i) 36

答案 1, 2, 3, 4, 9, 12, 18, 36

1 × 36 = 36

2 × 18 = 36

4 × 9 = 36

3 × 12 = 36

或

36 × 1 = 36

18 × 2 = 36

9 × 4 = 36

12 × 3 = 36

2. 写出下列数的第一个五倍数

(a) 5

答案: 5, 10, 15, 20, 25

5 × 1 = 5

5 × 2 = 10

5 × 3 = 15

5 × 4 = 20

5 × 5 = 25

(b) 8

答案: 8, 16, 24, 32, 40

8 × 1 = 8

8 × 2 = 16

8 × 3 = 24

8 × 4 = 32

8 × 5 = 40

(c) 9

答案：9, 18, 27, 36, 45

9 × 1 = 9

9 × 2 = 18

9 × 3 = 27

9 × 4 = 36

9 × 5 = 45

3. 将第一列的各项与第二列的各项配对。

4. 找出100以内的所有9的倍数。

答案 9, 18, 27, 26, 45, 54, 63, 72, 81, 90, 99

9 × 1 = 9

9 × 2 = 18

9 × 3 = 27

9 × 4 = 36

9 × 5 = 45

9 × 6 = 54

9 × 7 = 63

9 × 8 = 72

9 × 9 = 81

9 × 10 = 90

9 × 11 = 99

练习3.2

1. 任意两个

(a) 奇数的和是多少？

答案：任意两个奇数的和总是偶数。

例如：

3 + 3 = 6

5 + 7 = 12

7 + 9 = 16

(b) 偶数的和是多少？

答案：任意两个偶数的和总是偶数。

例如：

4 + 6 = 10

2 + 6 = 8

10 + 14 = 24

2. 判断以下陈述是真还是假

(a) 三个奇数的和是偶数。

答案：假

解释：三个奇数的和是奇数。

例如：

3 + 3 + 3 = 9

1 + 1 + 1 = 3

(b) 两个奇数和一个偶数的和是偶数。

答案：真

解释：两个奇数的和总是偶数。偶数加上偶数也是偶数。

例如：

3 (奇数) + 5 (奇数) + 2 (偶数) = 10 (偶数)

1 (奇数) + 7 (奇数) + 4 (偶数) = 12 (偶数)

(c) 三个奇数的乘积是奇数。

答案：真

解释：三个奇数的乘积是奇数。

例如：

3 × 1 × 3 = 9

5 × 1 × 3 = 15

(d) 如果一个偶数除以2，商总是奇数。

答案：假

解释：如果一个偶数除以2，商可以是偶数，也可以是奇数。它不总是奇数。相反，它可以是奇数或偶数。

例如：

10/2 = 5 (奇数)

20/2 = 10 (偶数)

(e) 所有质数都是奇数。

答案：假

解释：2 是一个质数，它是偶数。

(f) 质数没有因数。

答案：假

解释：质数有两个因数，1 和它本身。

例如：

质数7的因数是1和7。

(g) 两个质数的和总是偶数。

答案：假

解释：两个质数的和不总是偶数。它也可以是奇数。

例如：

2 (质数) + 3 (质数) = 5 (奇数)

(h) 2是唯一的偶质数。

答案：真

解释：2是唯一的偶质数。

(i) 所有偶数都是合数。

答案：假

解释：一个有超过两个因数的数称为合数。并非所有偶数都是合数，因为偶数2也是质数。

(j) 两个偶数的乘积总是偶数。

答案：真

解释：两个偶数的乘积总是偶数。

例如：

4 × 6 = 24 (偶数)

10 × 4 = 40 (偶数)

3. 数字13和31都是质数。这两个数字都有相同的数字1和3。找出100以内的所有这样的质数对。

答案：17和71，37和73，79和97

因此，100以内有三对这样的质数。

1. 17和71

2. 37和73

3. 79和97

4. 分别写出20以内的质数和合数。

答案：2, 3, 5, 7, 11, 13, 17, 和 19

20以内的质数和合数是2, 3, 5, 7, 11, 13, 17, 和 19。

5. 1到10之间最大的质数是多少？

答案：7

7是1到10之间最大的质数。

6. 将下列各数表示为两个奇质数的和。

(a) 44

答案：37 + 7 或 41 + 3 或 31 + 13

(b) 36

答案：31 + 5 或 29 + 7 或 23 + 13 或 17 + 19

(c) 24

答案：19 + 5 或 17 + 7 或 13 + 11

(d) 18

答案：11 + 7 或 5 + 13

7. 给出三对差为2的质数。

[备注：差为2的两个质数称为孪生素数]。

答案：3 和 5，11 和 13，17 和 19

我们可以给出任意三对差为2的质数。其他对包括5和7，29和31。

8. 下列哪些数字是质数？

(a) 23

答案：它是一个质数。

(b) 51

答案：它不是一个质数。51的因数是1, 3, 17, 和 51。

(c) 37

答案：它是一个质数。

(d) 26

答案：它不是一个质数。26的因数是1, 2, 13, 和 26。

9. 写出100以内七个连续的合数，使得它们之间没有质数。

答案 90, 91, 92, 93, 94, 95, 96

100以内没有质数的七个连续合数是90, 91, 92, 93, 94, 95, 和 96。

连续数是按从小到大的顺序连续排列的数字。

10. 将下列各数表示为三个奇质数的和

(a) 21

答案 3, 5, 13

21 = 3 + 5 + 13

其中，

3, 5, 和 13是奇质数

(b) 31

答案: 3, 5, 23

31 = 3 + 5 + 23

其中，

3, 5, 和 13是奇质数

(c) 53

答案 3, 7, 43

3 + 7 + 43 = 53

其中

3, 7, 和 43是奇质数

或

13, 17, 23

13 + 17 + 23 = 43

其中，

13, 17, 和 23是奇质数。

(d) 61

答案 13, 7, 41

13 + 7 + 41 = 61

其中，

13, 7, 和 41是奇质数。

11. 写出五对20以内的质数，它们的和能被5整除。

(提示：3+ 7 = 10)

答案

20以内的五对质数是

1. 2 + 3 = 5

2. 13 + 2 = 15

3. 17 + 3 = 20

4. 3 + 7 = 10

5. 13 + 17 = 30

其他对是

6. 11 + 19 = 30

12. 填空

(a) 只有一个因数的数称为质数。

(b) 有多个因数的数称为合数。

(c) 1 既不是质数也不是合数。

(d) 最小的质数是2。

(e) 最小的合数是4。

(f) 最小的偶数是2。

练习3.3

1. 使用整除性测试，确定下列哪些数字可以被2整除；

被3整除；被4整除；被5整除；被6整除；被8整除；被9整除；被10整除；被11整除（说“是”或“否”）

2. 使用整除性测试，确定下列哪些数字可以被整除

4；被8整除

如果一个数的最后两位数字可以被4整除，则该数可以被4整除。

如果一个数的最后三位数字可以被8整除，则该数可以被8整除。

(a) 572

答案：572可以被4整除，但不能被8整除。

解释：572的最后两位数字，即72，可以被4整除。因此，该数也可以被4整除。

572的最后三位数字，即572，不能被8整除。因此，该数也不能被8整除。

(b) 726352

答案：726352可以被4和8整除。

解释：726352的最后两位数字，即52，可以被4整除。因此，该数也可以被4整除。

726352的最后三位数字，即352，可以被8整除。因此，该数也可以被8整除。

(c) 5500

答案：5500可以被4整除，但不能被8整除。

解释：5500的最后两位数字，即00，可以被4整除。因此，该数也可以被4整除。

5500的最后三位数字，即500，不能被8整除。因此，该数也不能被8整除。

(d) 6000

答案：6000可以被4和8整除。

解释：6000的最后两位数字，即00，可以被4整除。因此，该数也可以被4整除。

6000的最后三位数字，即000，可以被8整除。因此，该数也可以被8整除。

(e) 12159

答案：12159不能被4和8整除。

解释：12159的最后两位数字，即59，不能被4整除。因此，该数也不能被4整除。

12159的最后三位数字，即159，不能被8整除。因此，该数也不能被8整除。

(f) 14560

答案：14560可以被4和8整除。

解释：14560的最后两位数字，即60，可以被4整除。因此，该数也可以被4整除。

14560的最后三位数字，即560，可以被8整除。因此，该数也可以被8整除。

(g) 21084

答案：21084可以被4整除，但不能被8整除。

解释：21084的最后两位数字，即84，可以被4整除。因此，该数也可以被4整除。

21084的最后三位数字，即084，不能被8整除。因此，该数也不能被8整除。

(h) 31795072

答案：31795072可以被4和8整除。

解释：31795072的最后两位数字，即72，可以被4整除。因此，该数也可以被4整除。

31795072的最后三位数字，即072，可以被8整除。因此，该数也可以被8整除。

(i) 1700

答案：1700可以被4整除，但不能被8整除。

解释：1700的最后两位数字，即00，可以被4整除。因此，该数也可以被4整除。

1700的最后三位数字，即700，不能被8整除。因此，该数也不能被8整除。

(j) 2150

答案：2150不能被4和8整除。

解释：2150的最后两位数字，即50，不能被4整除。因此，该数也不能被4整除。

2150的最后三位数字，即150，不能被8整除。因此，该数也不能被8整除。

因此，

(a), (b), (c), (d), (f), (g), (h), 和 (i) 可以被4整除。

(b), (d), (h), 和 (f) 可以被8整除。

3. 使用整除性测试，确定下列哪些数字可以被6整除

如果一个数同时能被2和3整除，那么它也能被6整除。个位数是0, 2, 4, 6, 和 8的数可以被2整除。如果数字之和是3的倍数，则该数可以被3整除。

(a) 297144

答案：它可以被6整除。

能被2整除

297144的个位数是4。因此，它可以被2整除。

能被3整除

2 + 9 + 7 + 1 + 4 + 4 = 27

27是3的倍数。

9 × 3 = 27

因此，它可以被3整除。

297144同时能被2和3整除。因此，它也能被6整除。

(b) 1258

答案：它不能被6整除。

能被2整除

1258的个位数是8。因此，它可以被2整除。

能被3整除

1 + 2 + 5 + 8 = 16

16不是3的倍数。

因此，它不能被3整除。

1258能被2整除但不能被3整除。因此，它不能被6整除。

(c) 4335

答案：它不能被6整除。

能被2整除

4335的个位数是5。因此，它不能被2整除。

能被3整除

4 + 3 + 3 + 5 = 15

15是3的倍数。

3 x 5 = 15

因此，它可以被3整除。

1258能被3整除但不能被2整除。因此，它不能被6整除。

(d) 61233

答案

它不能被6整除。

能被2整除

61233的个位数是3。因此，它不能被2整除。

能被3整除

6 + 1 + 2 + 3 + 3 = 15

15是3的倍数。

3 x 5 = 15

因此，它可以被3整除。

61233能被3整除但不能被2整除。因此，它不能被6整除。

(e) 901352

答案：它不能被6整除。

能被2整除

901352的个位数是2。因此，它可以被2整除。

能被3整除

9 + 0 + 1 + 3 + 5 + 2 = 20

20不是3的倍数。

因此，它不能被3整除。

901352能被2整除但不能被3整除。因此，它不能被6整除。

(f) 438750

答案：它可以被6整除。

能被2整除

438750的个位数是0。因此，它可以被2整除。

能被3整除

4 + 3 + 8 + 7 + 5 + 0 = 27

27是3的倍数。

9 × 3 = 27

因此，它可以被3整除。

438750同时能被2和3整除。因此，它也能被6整除。

(g) 1790184

答案：它可以被6整除。

能被2整除

1790184的个位数是4。因此，它可以被2整除。

能被3整除

1 + 7 + 9 + 0 + 1 + 8 + 4 = 30

30是3的倍数。

10 × 3 = 30

因此，它可以被3整除。

1790184同时能被2和3整除。因此，它也能被6整除。

(h) 12583

答案：它不能被6整除。

能被2整除

12583的个位数是3。因此，它不能被2整除。

能被3整除

1 + 2 + 5 + 8 + 3 = 19

19不是3的倍数。

因此，它不能被3整除。

12583既不能被2整除，也不能被3整除。因此，它不能被6整除。

(i) 639210

答案：它可以被6整除。

能被2整除

639210的个位数是0。因此，它可以被2整除。

能被3整除

6 + 3 + 9 + 2 + 1 + 0 = 21

21是3的倍数。

7 × 3 = 21

因此，它可以被3整除。

639210同时能被2和3整除。因此，它也能被6整除。

(j) 17852

答案：它不能被6整除。

能被2整除

17852的个位数是2。因此，它可以被2整除。

能被3整除

1 + 7 + 8 + 5 + 2 = 23

23不是3的倍数。

因此，它不能被3整除。17852能被2整除但不能被3整除。因此，它不能被6整除。

4. 使用整除性测试，确定下列哪些数字可以被11整除

如果一个数从右边开始的奇数位数字之和与偶数位数字之和的差是0或11的倍数，则该数可以被11整除。

(a) 5445

答案：它可以被11整除。

奇数位数字之和：5 + 4 = 9

偶数位数字之和：4 + 5 = 9

差：9 - 9 = 0

因此，5445可以被11整除。

(b) 10824

答案：它可以被11整除。

奇数位数字之和：4 + 8 + 1 = 13

偶数位数字之和：2 + 0 = 2

差：13 - 2 = 11

11可以被11整除。

11 × 1 = 11

因此，10824可以被11整除。

(c) 7138965

答案：它不能被11整除。

奇数位数字之和：5 + 9 + 3 + 7 = 24

偶数位数字之和：6 + 8 + 1 = 15

差：24 - 15 = 9

9不能被11整除。

因此，7138965不能被11整除。

(d) 70169308

答案：它可以被11整除。

奇数位数字之和：8 + 3 + 6 + 0 = 17

偶数位数字之和：0 + 9 + 1 + 7 = 17

差：17 - 17 = 0

因此，70169308可以被11整除。

(e) 10000001

答案：它可以被11整除。

奇数位数字之和：1 + 0 + 0 + 0 = 1

偶数位数字之和：0 + 0 + 0 + 1 = 1

差：1 - 1 = 0

因此，10000001可以被11整除。

(f) 901153

答案：它可以被11整除。

奇数位数字之和：3 + 1 + 0 = 4

偶数位数字之和：5 + 1 + 9 = 15

差：15 - 4 = 11

11可以被11整除。

11 × 1 = 11

因此，901153可以被11整除。

5. 在下列各数的空白处填入最小和最大的数字，使所得的数能被3整除

如果数字之和能被3整除，则该数可以被3整除。

(a) __ 6724

答案：2 和 8

解释：假设空白处为a。

a + 6 + 7 + 2 + 4 = a + 19

最小:

在最小的情况下，我们需要考虑最接近的数。

最接近19且能被3整除的数是21。

a + 19 = 21

a = 21 - 19

a = 2

因此，2是使该数能被3整除的最小数字。

最大

最远离19且能被3整除的数是27。

如果我们考虑30，则差距将超过10。我们需要考虑数字之间的差距小于9。

a + 19 = 27

a = 27 - 19

a = 8

因此，8是使该数能被3整除的最大数字。

(b) 4765 __ 2

答案：0 和 9

解释：假设空白处为a。

4 + 7 + 6 + 5 + a + 2 = a + 24

最小:

在最小的情况下，我们需要考虑最接近的数。

最接近24的数就是24本身。因为24也能被3整除。

a + 24 = 24

a = 24 - 24

a = 0

因此，0是使该数能被3整除的最小数字。

最大

最远离24且能被3整除的数是33。

如果我们考虑36，则差距将超过10。我们需要考虑数字之间的差距小于或等于9。

a + 24 = 33

a = 33 - 24

a = 9

因此，9是使该数能被3整除的最大数字。

6. 在下列各数的空白处填入一个数字，使所得的数能被11整除

如果一个数从右边开始的奇数位数字之和与偶数位数字之和的差是0或11的倍数，则该数可以被11整除。

(a) 92 __ 389

答案：8

设空白处的数字为a。

奇数位数字之和：9 + 3 + 2 = 14

偶数位数字之和：8 + a + 9 = 17 + a

差 = (17 + a) - 14

= 3 + a

最接近3且能被11整除的数是11。

3 + a = 11

a = 8

我们不能取0，因为数字可能变为负数。

3 + a = 0, a = -3

这不是所需的数字。我们只需要正数。

(b) 8 __ 9484

答案：6

设空白处的数字为a。

奇数位数字之和：4 + 4 + a = 8 + a

偶数位数字之和：8 + 9 + 8 = 25

差 = 25 - (8 + a)

= 25 - 8 - a

= 17 - a

最接近能被11整除的数是11。

17 - a = 11

a = 17 - 11

a = 6

我们不能取22，因为数字(a)会是负数。取22时，我们可能会得到一个负数。

17 - a = 22

a = -5

这不是所需的数字。我们只需要正数。

如果取0，我们可能会得到一个两位数。我们只需要在空白处填入一个数字。

17 - a = 0, a = 17

这也不符合要求。

练习3.4

1. 求下列各数的公因数

(a) 20 和 28

答案 1, 2, 4

20的因数：1, 2, 4, 5, 10, 20

28的因数：1, 2, 4, 7, 14, 28

这两个数有1, 2, 和 4是公有的。

(b) 15 和 25

答案 1, 5

15的因数：1, 3, 5, 15

25的因数：1, 5, 25

这两个数有1和5是公有的。

(c) 35 和 50

答案 1, 5

35的因数：1, 5, 7, 35

50的因数：1, 2, 5, 10, 25, 50

这两个数有1和5是公有的。

(d) 56 和 120

答案: 1, 2, 4, 8

56的因数：1, 2, 4, 7, 8, 14, 28, 56

120的因数：1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

这两个数有1, 2, 4, 和 8是公有的。

2. 求下列各数的公因数

(a) 4, 8 和 12

答案 1, 2, 4

4的因数：1, 2, 4

8 的因子：1、2、4、8

12的因数：1, 2, 3, 4, 6, 12

这三个数有1, 2, 和 4是公有的。

(b) 5, 15 和 25

答案 1, 5

5的因数：1, 5

15的因数：1, 3, 5

25的因数：1, 5, 25

这三个数有1和5是公有的。

3. 求下列各数的前三个公倍数

(a) 6 和 8

答案 24, 48, 72

公倍数是指能同时被6和8整除的数。

6的倍数：6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90

8的倍数：8, 16, 24, 32, 40, 48, 56, 64, 72, 80

因此，前三个公倍数是24, 48, 和 72。

(b) 12 和 18

答案 36, 72, 108

公倍数是指能同时被12和18整除的数。

12的倍数：12, 24, 36, 48, 60, 72, 84, 96, 108, 120

18的倍数：18, 36, 54, 72, 90, 108, 126, 144, 162, 180

因此，前三个公倍数是36, 72, 和 108。

4. 写出100以内所有是3和4公倍数的数。

答案 12, 24, 36, 48, 60, 72, 84, 96.

3的倍数：3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99

4的倍数：4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96

因此，100以内3和4的公倍数是12, 24, 36, 48, 60, 72, 84, 和 96。

5. 下列哪些数字是互质数？

只有公因数1的两个数称为互质数。

(a) 18 和 35

答案：它是一个互质数。

18和35只有1是公因数。

18的因数：1, 2, 3, 6, 9, 18

35的因数：1, 5, 7, 35

(b) 15 和 37

答案：它是一个互质数。

15和37只有1是公因数。

15的因数：1, 3, 5, 15

37的因数：1, 37

(c) 30 和 415

答案：它不是一个互质数。

30的因数：1, 2, 3, 5, 6, 10, 15, 30

415的因数：1, 5, 83, 415

30和415有公因数1和5。因此，它不是一个互质数。

(d) 17 和 68

答案：它不是一个互质数。

17的因数：1, 17

68的因数：1, 2, 4, 17, 34, 68

17和68有公因数1和17。因此，它不是一个互质数。

(e) 216 和 215

答案：它是一个互质数。

216的因数：1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216。

215的因数：1, 5, 45, 215

(f) 81 和 16

答案：它是一个互质数。

81的因数：1, 3, 9, 27, 81

16的因数：1, 2, 4, 8, 16

6. 一个数同时能被5和12整除。它还能被哪个数整除？

答案 60

12和5是互质数，因为它们只有一个公因数1。因此，如果一个数同时能被5和12整除，它就能被它们的乘积，即12 × 5 = 60整除。

7. 一个数能被12整除。它还能被哪些数整除？

答案: 1, 2, 3, 4, 6, 12

如果一个数能被12整除，它也能被12的因数整除。

12的因数：1, 2, 3, 4, 6, 和 12

练习 3.5

1. 下列哪些陈述是真？

(a) 如果一个数能被3整除，它必须能被9整除。

答案：假

解释：如果一个数能被3整除，它不一定能被9整除。

例如：

数字：6, 12, 15, 21, 24

这些数能被3整除，但不能被9整除。

(b) 如果一个数能被9整除，它必须能被3整除。

答案：真

解释：如果一个数能被9整除，它总能被3整除。

例如：

数字：9, 18, 27, 36, 45

这些数能被9整除。因此，也能被3整除。

(c) 一个数能被3和6同时整除，则它能被18整除。

答案：假

解释：如果一个数能被3和6同时整除，它不一定能被18整除。

例如：

数字：12, 24, 30, 42

上述数字能被3和6整除，但不能被18整除。

在某些情况下，可能是真的。

例如：

数字：18, 36, 54, 72

这些数字能被3, 6, 以及18整除。

(d) 如果一个数同时能被9和10整除，那么它必须能被90整除。

答案：真

解释：9和10是互质数。因此，如果一个数同时能被9和10整除，它必须能被它们的乘积，即9 × 10 = 90整除。

例如：

90, 180, 270, 360

(e) 如果两个数是互质数，其中至少一个必须是质数。

答案：假

解释：只有1是公因数的数是互质数。任何类型的数都可以是互质数，如果它们的公因数是1。

例如：

9 和 20

9的因数：1, 3, 9

20的因数：1, 2, 5, 10, 20

它们只有1是公因数，而且它们都不是质数。

(f) 所有能被4整除的数也必须能被8整除。写出16, 28, 38的质因数分解。

答案：假

解释：如果一个数能被4整除，它不一定能被8整除。

例如：

数字：12, 16, 20, 24, 28, 32, 36

这些数都能被4整除。但在这些数中，只有16, 24, 和 32能被8整除。

(g) 所有能被8整除的数也必须能被4整除。

答案：真

解释：如果一个数能被8整除，它也能被4整除。

8的因数：1, 2, 4, 和 8

因此，如果一个数能被8整除，它总是能被它的因数整除。

例如：

数字：8, 16, 24, 32, 40, 48, 56

这些数既能被4整除，也能被8整除。

(h) 如果一个数分别整除两个数，那么它必须整除它们的和。

答案：真

解释：如果一个数分别整除两个数，那么它必须整除它们的和。

例如：

数字：4

4整除8和16。

和：8 + 16 = 24

因此，数字4分别整除8和16，并且也整除它们的和（8 + 16 = 24）。

(i) 如果一个数整除两个数的和，那么它必须分别整除这两个数。

答案：假

解释：如果一个数整除两个数的和，它不一定分别整除这两个数。

例如：

数字：6

6整除24。

但是，它不整除它们的和（10 + 14）。

只有在某些情况下才可能。

例如：

6整除24，也分别整除18和6。

因此，上述条件仅在某些情况下为真。

2. 这里有两个不同的60的因数树。写出缺失的数字。

(a)

2 × 3 = 6

5 × 2 = 10

(b)

30 × 2 = 60

10 × 3 = 30

2 × 5 = 10

3. 合数的质因数分解中不包括哪些因数？

答案：每个数的公因数是1和它本身。因此，合数的质因数分解中不包括因数1和它本身。

4. 写出最大的四位数，并将其表示为其质因数。

答案 9999

9999是最大的四位数。

9999的质因数 3, 3, 11, 101

101 × 11 × 3 × 3 = 9999

9999 = 9 × 1111

9999 = (3 × 3) × (101 × 11)

5. 写出最小的五位数，并将其表示为其质因数形式。

答案 10000

10000是最小的五位数。

10000的质因数 2, 2, 2, 2, 5, 5, 5, 5

2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 = 10000

10000 = 4 × 2500

10000 = (2 × 2) × (25 × 100)

10000 = (2 × 2) × (5 × 5 × 4 × 25)

10000 = (2 × 2) × (5 × 5 × 2 × 2 × 5 × 5)

10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5

6. 找出1729的所有质因数，并按升序排列。现在，陈述两个连续质因数之间是否存在任何关系。

答案: 7, 13, 19

1729的质因数是7, 13, 和 19。

7 × 13 × 19 = 1729

有三个质因数。它们之间的关系是

13 - 7 = 6

19 - 13 = 6

因此，升序排列的三个连续质因数相差6。

注意：因数和质因数是不同的术语。质因数不包括因数1和它本身。

7. 三个连续数的乘积总是能被6整除。通过一些例子来验证这个陈述。

答案：三个连续数总是包含一个能被2或3整除的数。这三个数的乘积能同时被2和3整除。因此，如果一个数能被2和3同时整除，它就能被6整除。

示例 1: 1, 2, 3

1 × 2 × 3 = 6

示例 2 3, 4, 5

3 × 4 × 5 = 60

示例 3: 6, 7, 8

6 × 7 × 8 = 336

示例 4: 8, 9, 10

8 × 9 × 10 = 720

8. 两个连续奇数的和能被4整除。通过一些例子来验证这个陈述.

答案：奇数的和总是偶数。同样，两个连续奇数的和能被4整除。

例如：

1 和 3

1 + 3 = 4

4能被4整除。

3 和 5

3 + 5 = 8

8能被4整除。

5 和 7

5 + 7 = 12

12能被4整除。

7 和 9

7 + 9 = 16

16能被4整除。

9 和 11

9 + 11 = 20

20能被4整除。

9. 在下列哪些表达式中，进行了质因数分解？

质因数是能反复除以该数，直到商不能再被该数整除的因数。

(a) 24 = 2 × 3 × 4

答案：这不是正确的质因数分解。因为4的因数是(2, 2)。

正确： 24 = 2 × 3 × 2 × 2

(b) 56 = 7 × 2 × 2 × 2

答案：这是正确的质因数分解。

(c) 70 = 2 × 5 × 7

答案：这是正确的质因数分解。

(d) 54 = 2 × 3 × 9

答案：这不是正确的质因数分解。因为9的因数是(3, 3)。

正确： 24 = 2 × 3 × 3 × 3

10. 判断25110是否能被45整除。

[提示：5和9是互质数。测试该数能否被5和9整除]。

答案

45 = 9 × 5

由于5和9是互质数。因此，如果一个数能被5和9整除，它就能被它们的乘积（9 × 5 = 45）整除。

能被9整除

如果一个数的各位数字之和能被9整除，则该数本身能被9整除。

2 + 5 + 1 + 1 + 0 = 9

9 × 1 = 9

9能被9整除。

因此，25110能被9整除。

能被5整除

如果一个数的个位数是0或5，则该数能被5整除。25110的个位数是0。因此，它能被5整除。

25110同时能被5和9整除。因此，它也能被它们的乘积（9 × 5 = 45）整除。

11. 18同时能被2和3整除。它也能被2 × 3 = 6整除。类似地，一个数同时能被4和6整除。我们能说这个数也一定能被4 × 6 = 24整除吗？如果不能，请举例说明。

答案：不能。

如果一个数同时能被4和6整除，并不一定能被24整除。

例如：

12, 36, 60

上述数字能被4和6整除，但不能被24整除。

12. 我是最小的数，有四个不同的质因数。你能找到我吗？

答案：最小数的四个不同质因数必须是最小的。设因数为2, 3, 5, 7。

数：2 × 3 × 5 × 7

数字：210 我们不能取4和6作为因数，因为它们包含重复的数字2和3。

练习 3.6

1. 求下列各数的最大公约数

两个或多个给定数的最大公约数 (HCF) 是它们公因数中最大的（或最高的）。

(a) 18, 48

答案: 6

18的因数：2 × 3 × 3

48的因数：2 × 2 × 2 × 2 × 3

18和48的公因数是：2 × 3

因此，最大公约数 = 6

(b) 30, 42

答案: 6

30的因数：2 × 3 × 5

42的因数：2 × 3 × 7

30和42的公因数是：2 × 3

因此，最大公约数 = 6

(c) 18, 60

答案 6

18的因数：2 × 3 × 3

60的因数：2 × 3 × 2 × 5

18和60的公因数是：2 × 3

因此，最大公约数 = 6

(d) 27, 63

答案 9

27的因数：3 × 3 × 3

63的因数：3 × 3 × 7

27和63的公因数是：3 × 3

因此，最大公约数 = 9

(e) 36, 84

答案

36的因数：2 × 2 × 3 × 3

84的因数：2 × 2 × 3 × 7

36和84的公因数是：2 × 2 × 3

因此，最大公约数 = 12

(f) 34, 102

答案 34

34的因数：2 × 17

102的因数：2 × 3 × 17

34和102的公因数是：2 × 17

因此，最大公约数 = 34

(g) 70, 105, 175

答案 35

70的因数：2 × 7 × 5

105的因数：7 × 5 × 3

175的因数：7 × 5 × 5

70, 105, 和 175的公因数是：7 × 5

因此，最大公约数 = 35

(h) 91, 112, 49

答案 7

91的因数：7 × 13

112的因数：2 × 2 × 2 × 2 × 7

49的因数：7 × 7

91, 112, 和 49的公因数是：7

因此，最大公约数 = 7

(i) 18, 54, 81

答案 9

18的因数：2 × 3 × 3

54的因数：2 × 3 × 3 × 3

81的因数：3 × 3 × 3 × 3

18, 54, 和 81的公因数是：3 × 3

因此，最大公约数 = 9

(j) 12, 45, 75

答案 3

18的因数：2 × 2 × 3

45的因数：5 × 3 × 3

75的因数：5 × 5 × 3

12, 45, 和 75的公因数是：3

因此，最大公约数 = 3

2. 任意两个

(a) 连续数的最大公约数是多少？

答案 1

任意两个连续数之间只有一个公因数，即1。因此，任意两个连续数的最大公约数是1。

例如：

1 和 2

3 和 4

5 和 6

6 和 7

(b) 连续偶数的最大公约数是多少？

答案 2

任意两个连续偶数之间只有一个公因数，即2。因此，任意两个连续偶数的最大公约数是2。

例如：

2 和 4

4 和 6

6 和 8

8 和 10

(c) 连续奇数的最大公约数是多少？

答案 1

任意两个连续奇数之间只有一个公因数，即1。因此，任意两个连续奇数的最大公约数是1。

例如：

1 和 3

5 和 7

7 和 9

11 和 13

3. 互质数4和15的最大公约数通过因数分解找到如下：4 = 2 × 2 和 15 = 3 × 5 因为没有共同的质因数，所以4和15的最大公约数是0。答案正确吗？如果不正确，正确的最大公约数是多少？

解答：不正确

正确的答案是：1

任何两个数的最大公约数都不可能为0。任何两个互质数的公因数是1。因此，没有共同质因数的这类数的最大公约数总是1。

练习 3.7

1. Renu购买了两袋重75公斤和69公斤的化肥。找出能够精确次数衡量化肥重量的最大重量值。

解决方案

两袋化肥的重量 = 75公斤和69公斤

最大重量值 = HCF (75, 69)

75的因数：5 × 5 × 3

69的因数：3 × 23

75和69的公因数是：3

因此，最大公约数 = 3

能够精确次数衡量75公斤和69公斤化肥重量的最大重量值是3公斤。

2. 三个男孩从同一点一起迈步。他们的步长分别为63厘米、70厘米和77厘米。每个人应该走多远，才能让他们都走完完整的步数？

解决方案

第一个男孩的步长 = 63厘米

第二个男孩的步长 = 70厘米

第三个男孩的步长 = 77厘米

最小距离 = LCM (63, 70, 77)

LCM = 3 × 7 × 3 × 10 × 11

LCM = 6930

因此，每个人应该走的最小距离是6930厘米，这样他们都能走完完整的步数。

3. 一个房间的长、宽、高分别为825厘米、675厘米和450厘米。找出能够精确测量房间三个尺寸的最长卷尺。

解决方案

房间的长度 = 825厘米

房间的宽度 = 675厘米

房间的高度 = 450厘米

最长卷尺 = HCF (825, 675, 450)

825的因数：5 × 5 × 3 × 11

675的因数：5 × 5 × 3 × 3 × 3

450的因数：5 × 5 × 3 × 3 × 2

825, 675, 450的公因数是：5 × 5 × 3

因此，HCF = 75

能够精确测量房间三个尺寸的最长卷尺长度是75厘米。

4. 找出能被6, 8和12整除的最小三位数。

解决方案

为了找到最小的三位数，我们需要找到LCM。

6, 8和12的LCM（最低公倍数）是

LCM = 3 × 2 × 2 × 2

LCM = 24

最小的三位数应该大于100。最接近100的24的倍数是24 × 5 = 120。

因此，能被6, 8和12整除的最小三位数是120。

5. 找出能被8, 10和12整除的最大三位数。

解答：最大的三位数是999。

LCM (8, 10, 12)

LCM = 2 × 2 × 2 × 5 × 3

= 120

最接近999的120的三位数倍数是120 × 8 = 960。

因此，能被8, 10和12整除的最大三位数是960。

6. 三个不同路口的交通灯分别以48秒、72秒和108秒的间隔变绿。如果它们在早上7点同时变绿，那么它们将再次同时变绿的时间是？

解决方案

LCM (48, 72, 108)

LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3

= 432

= 60 × 7 + 12

= 7分钟12秒

因此，三个不同路口的交通灯将同时变绿的时间是早上7点7分钟12秒。

7. 三个油罐分别装有403升、434升和465升柴油。找出能够精确次数衡量这三个油罐柴油容量的容器的最大容量。

解决方案

最大容量 = HCF (403, 434, 465)

403的因数：13 × 31

434的因数：14 × 31

465的因数：15 × 31

公因数：31

因此，能够精确次数衡量这三个油罐柴油容量的容器的最大容量是31升。

8. 找出能被6, 15和18整除，且在每种情况下余数为5的最小数字。

解答：LCM (6, 5, 18)

LCM = 2 × 3 × 3 × 5

= 90

最小数字 = 90

余数为5的最小数字 = 90 + 5 = 95

因此，95是能被6, 15和18整除，且在每种情况下余数为5的最小数字。

9. 找出能被18, 24和32整除的最小四位数。

解答：最小的四位数是1000。

LCM (18, 24, 32)

LCM = 2 × 2 × 2 × 2 × 2 × 3 × 3

LCM = 288

最接近1000的288的倍数是288 × 4 = 1152

因此，能被18, 24和32整除的最小四位数是1152。

10. 求下列各数的LCM

(a) 9 和 4 解答 36

LCM = 3 × 3 × 2 × 2

= 9 × 4

= 36

(b) 12 和 5

解决方案 60

LCM = 3 × 2 × 2 × 5

= 60

(c) 6 和 5

解决方案 30

LCM = 3 × 2 × 5

= 30

(d) 15 和 4

解决方案 60

LCM = 3 × 5 × 2 × 2

= 60

观察得到的LCM中的共同属性。LCM是否是每个情况下的两个数的乘积？

答案：是的，如果这两个数是互质数。

上述两个数是互质数，即只有一个公因数1。这类数的LCM是它们的乘积。

11. 求下列各数的LCM，其中一个数是另一个数的因数。

(a) 5, 20

答案 20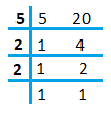

LCM = 5 × 2 × 2

LCM = 20

(b) 6, 18

答案 18

LCM = 2 × 3 × 3

LCM = 18

(c) 12, 48

答案 48

LCM = 2 × 3 × 2 × 2 × 2

LCM = 48

(d) 9, 45

答案 45

LCM = 3 × 3 × 5

LCM = 45

你从得到的结果中观察到了什么？

解答：我们观察到上述两数的LCM是较大的那个数。这意味着如果一个数是另一个数的因数，那么LCM将是较大的那个数。