NCERT 10年级第13章解决方案：表面积和体积

练习 13.1

除非另有说明，否则取 π = 22/7

1. 将两个体积均为64 cm³的立方体端对端连接起来。求所得长方体的表面积。

解决方案

1个立方体的体积 = 64 cm³

a³ = 64

a = 4 cm

每个立方体的边长 = 4 cm

连接两个立方体时，长方体的长度 = a = 4 cm

连接两个立方体时，长方体的宽度 = a = 4 cm

连接两个立方体时，长方体的高度 = 2a = 8 cm

立方体的总表面积 = 2(lb + bh + hl)

= 2(4 × 4 + 4 × 8 + 8 × 4)

= 2(16 + 32 + 32)

= 2(80)

= 160 cm²

2. 一个容器是空心半球，上面装有空心圆柱体。半球的直径为14厘米，容器的总高度为13厘米。求容器的内表面积。

解决方案

圆柱体和半球的半径 = 14/2 = 7 cm

圆柱体的侧面积 = 2πrh

= 2 × 22/7 × 7 × 6

= 264 cm²

半球的侧面积 = 2πr²

= 2 × 22/7 × 7 × 7

= 308 cm²

容器的内表面积 = 圆柱体侧面积 + 半球侧面积

= 264 + 308

= 572 cm²

3. 一个玩具的形状是半径为3.5厘米的圆锥，安装在相同半径的半球上。玩具的总高度为15.5厘米。求玩具的总表面积。

解决方案

圆锥的高度 = h = 玩具高度 - 半球半径

= 15.5 - 3.5

= 12 cm

圆锥的斜高 = l = √(h² + r²)

= √(12² + 3.5²)

= √(144 + 12.25)

= √(156.25)

= 12.5 cm

圆锥的侧面积 = πrl

= 22/7 × 3.5 × 12.5

= 137.5 cm²

半球的侧面积 = 2πr²

= 2 × 22/7 × 3.5 × 3.5

= 77 cm²

玩具的总表面积 = 圆锥侧面积 + 半球侧面积

= 137.5 + 77

= 214.5 cm²

4. 一个边长为7厘米的立方体块上方有一个半球。半球可以有的最大直径是多少？求固体的表面积。

解决方案

因为立方体的每条边长为7厘米。因此，半球可能的最大直径为7厘米。

半球的侧面积 = 2πr²

= 2 × 22/7 × 7/2 × 7/2

= 77 cm²

半球底面积 = πr²

= 22/7 × 7/2 × 7/2

= 38.5 cm²

正方形的表面积 = 6a²

= 6 × 7²

= 6(49)

= 294 cm²

给定固体的总表面积 = 立方体表面积 + 半球侧面积 - 半球底面积

= 294 + 77 - 38.5

= 294 + 38.5

= 332.5 cm²

5. 从一个立方体木块的一个面上切出一个半球形凹陷，使得半球的直径l等于立方体的边。确定剩余固体的表面积。

解决方案

半球的侧面积 = 半球的侧面积 = 2πr²

= 2 × 22/7 × l/2 × l/2

= 11l²/7 平方单位

半球底面积 = πr²

= 22/7 × l/2 × l/2

= 11l²/14 平方单位

立方体的表面积 = 6l² 平方单位

固体的总表面积 = 立方体表面积 + 半球侧面积 - 半球底面积

= 6l² + 11l²/7 + 11l²/14

= (154l² + 22l² + 11l²)/14

= (187l²)/14 平方单位

6. 一个药胶囊的形状是圆柱体，两端连接着半球（见图13.10）。整个胶囊的长度为14毫米，直径为5毫米。求其表面积。

解决方案

圆柱部分的长度 = 胶囊长度 - 2 × 半球端半径

= 14 - 5

= 9 mm

圆柱体的侧面积 = 2πrh

= 2 × 22/7 × 5/2 × 9

= 990/7 mm²

一个半球的侧面积 = 2πr²

= 2 × 22/7 × 5/2 × 5/2

= 275/7 mm²

两个半球的侧面积 = 2 × 275/7 = 550/7 mm²

胶囊的总表面积 = 两个半球侧面积 + 圆柱体侧面积

= 550/7 + 990/7

= 1540/7

= 220 mm²

7. 一个帐篷的形状是圆柱体，顶部是圆锥形。如果圆柱部分的高度和直径分别为2.1米和4米，顶部斜高为2.8米，求制作帐篷所用帆布的面积。同时，以每平方米500卢比的价格计算帐篷帆布的成本。（注意帐篷底部不覆盖帆布。）

解决方案

圆锥顶部的侧面积 = πrl

= 22/7 × 4/2 × 2.8

= 17.6 m²

圆柱底部侧面积 = 2πrh

= 2 × 22/7 × 4/2 × 2.1

= 26.4 m²

总帆布用量 = 圆锥侧面积 + 圆柱体侧面积

= 17.6 + 26.4

= 44 m²

每平方米帆布价格 = 500卢比

44平方米帆布的价格 = 500 × 44

= 22000卢比

因此，帐篷帆布的成本是22000卢比。

8. 从一个高2.4厘米，直径1.4厘米的实心圆柱体中，挖出一个相同高度和相同直径的圆锥形空腔。求剩余固体的总表面积（精确到最接近的平方厘米）。

解决方案

圆柱体半径 = 1.4/2 = 0.7 cm

圆锥形空腔的斜高 = l = √(h² + r²)

= √(2.4² + 0.7²)

= √(5.76 + 0.49)

= √(6.25)

= 2.5 cm

圆锥的侧面积 = πrl

= 22/7 × 0.7 × 2.5

= 5.5 cm²

圆柱体的侧面积 = 2πrh

= 2 × 22/7 × 0.7 × 2.4

= 10.56 cm²

圆柱体底面积 = πr²

= 22/7 × 0.7 × 0.7

= 1.54 cm²

剩余固体的总表面积 = 圆锥侧面积 + 圆柱体侧面积 + 圆柱体底面积

= 5.5 + 10.56 + 1.54

= 17.6 cm²

9. 一个木制物品由一个实心圆柱体的两端挖出半球制成（如图13.11所示）。如果圆柱体的高度为10厘米，底面半径为3.5厘米，求该物品的总表面积。

解决方案

圆柱体的半径 = 半球的半径

一个半球的侧面积 = 2πr²

= 2 × 22/7 × 3.5 × 3.5

= 77 cm²

圆柱体的侧面积 = 2πrh

= 2 × 22/7 × 3.5 × 10

= 220 cm²

给定固体的总表面积 = 2 × 一个半球侧面积 + 圆柱体侧面积

= 2 × 77 + 220

= 154 + 220

= 374 cm²

练习 13.2

除非另有说明，否则取 π = 22/7

1. 一个固体是圆锥形，底部在半球上，两个半径均为1厘米，圆锥高度等于其半径。求以π表示的固体体积。

解决方案

圆锥体积 = 1/3 × πr²h

= 1/3 × 22/7 × 1² × 1

= 22/21 cm³

半球体积 = 2/3 × πr³

= 2/3 × 22/7 × 1³

= 44/21 cm³

给定固体的总体积 = 圆锥体积 + 半球体积

= 22/21 + 44/21

= 66/21

= 22/7 = π cm³

2. 工程专业的学生瑞秋被要求用薄铝板制作一个模型，该模型形状为圆柱体，两端连接着两个圆锥体。模型的直径为3厘米，长度为12厘米。如果每个圆锥体的高度为2厘米，求瑞秋制作的模型所含空气的体积。（假设模型的外部尺寸和内部尺寸大致相同。）

解决方案

圆柱体的半径 = 圆锥体的半径 = 3/2 = 1.5 cm

圆柱体的长度 = H = 12 - 2 - 2 = 8 cm

一个圆锥的体积 = 1/3 × πr²h

= 1/3 × 22/7 × 1.5 × 1.5 × 2

= 33/7 cm³

圆柱体的体积 = πr²H

= 22/7 × 1.5 × 1.5 × 8

= 396/7 cm²

模型的总体积 = 圆柱体体积 + 2 × 圆锥体体积

= 396/7 + 2 × 33/7

= 396/7 + 66/7

= 462/7

= 66 cm³

3. 一个 gulaab jamun 含有约30%体积的糖浆。每件 gulaab jamun 的形状是圆柱体，两端为半球形，长度为5厘米，直径为2.8厘米（见图13.15）。求45个 gulaab jamuns 中大约有多少糖浆？

解决方案

两个半球端的半径 = 圆柱体的半径 = 2.8/2 = 1.4 cm

圆柱部分的体积 = πr²h

= 22/7 × 1.4² × (5 - 1.4 - 1.4)

= 22 × 0.28 × 2.2

= 13.552 cm³

一个半球端的体积 = 2/3 × πr³

= 2/3 × 22/7 × 1.4³

= 17.248/3 cm³

一个 gulaab jamun 的体积 = 2 × 一个半球端的体积 + 圆柱部分体积

= 2 × 17.248/3 + 13.552

= 34.496/3 + 13.552

= (34.496 + 40.656)/3

= 75.152/3 cm³

一个 gulaab jamun 中的糖浆体积 = 30/100 × 75.152/3

= 7.5152 cm³

45个 gulaab jamuns 中的糖浆体积 = 7.5152 × 45

= 338.184 cm³

4. 一个用木头制成的笔筒，形状是带四个圆锥形凹槽的立方体，用于存放笔。立方体的尺寸为15厘米×10厘米×3.5厘米。每个凹槽的半径为0.5厘米，深度为1.4厘米。求整个笔筒的木材体积（见图13.16）。

解决方案

立方体的体积 = l × b × h

= 15 × 10 × 3.5

= 525 cm³

一个圆锥形凹槽的体积 = 1/3 × πr²h

= 1/3 × 22/7 × 0.5² × 1.4

= 1.1/3 cm³

笔筒的木材体积 = 立方体体积 - 4 × 圆锥形凹槽体积

= 525 - 4.4/3

= (1575 - 4.4)/3

= 1570.6/3

= 523.533 cm³

5. 一个容器呈倒置的圆锥形。高度为8厘米，顶部（开口处）半径为5厘米。它装满了水。当铅球（每个铅球都是半径为0.5厘米的球体）放入容器时，四分之一的水流出。求放入的铅球数量。

解决方案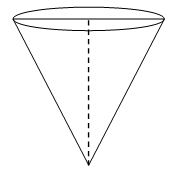

圆锥中的水量 = 圆锥体积 = 1/3 × πRr²h

= 1/3 × 22/7 × 5² × 8

= 4400/21 cm³

从容器中流出的水量 = 1/4 × 4400/21

= 1100/21 cm³

一个铅球的体积 = 4/3 × πr³

= 4/3 × 22/7 × 0.5³

= 11/21 cm³

放入的铅球数量 = 流出的水量/一个铅球的体积

= 1100/21 × 21/11

= 100

因此，放入了100个铅球。

6. 一根实心铁杆由一个高220厘米、底径24厘米的圆柱体组成，其顶部还有一个高60厘米、半径8厘米的圆柱体。求铁杆的质量，已知1立方厘米的铁的质量约为8克。（使用π = 3.14）

解决方案

顶部圆柱体的体积 = πr²h

= 3.14 × 8² × 60

= 12057.6 cm³

底部圆柱体的体积 = πR²H

= 3.14 × (24/2)² × 220

= 99475.2 cm³

铁杆的体积 = 顶部圆柱体体积 + 底部圆柱体体积

= 12057.6 + 99475.2

= 111532.8 cm³

1立方厘米铁的质量 = 8克

铁杆的质量 = 111532.8 × 8

= 892262.4 cm³

7. 将一个高120厘米、半径60厘米的直圆锥体，与一个半径60厘米的半球体组成一个实心体，该实心体竖直放置在一个装满水的直圆柱体中，使其触及底部。若圆柱体的半径为60厘米，高为180厘米，求圆柱体中剩余的水的体积。

解决方案

圆柱体中的水量 = 圆柱体体积 = πr²H

= 22/7 × 60² × 180

= 14256000/7 cm³

圆锥体积 = 1/3 × πr²h

= 1/3 × 22/7 × 60² × 120

= 3168000/7 cm³

半球体积 = 2/3 × πr³

= 2/3 × 22/7 × 60³

= 3168000/7 cm³

圆柱体中剩余的水的体积 = 圆柱体体积 - 圆锥体积 - 半球体积

= 14256000/7 - 3168000/7 - 3168000/7

= 7920000/7 cm³ 或 7.92/7 m³

8. 一个球形玻璃容器有一个圆柱形颈，长8厘米，直径2厘米；球形部分的直径为8.5厘米。通过测量其容水量，一个孩子发现其体积为345立方厘米。以π=3.14计算，检查她是否正确。

解决方案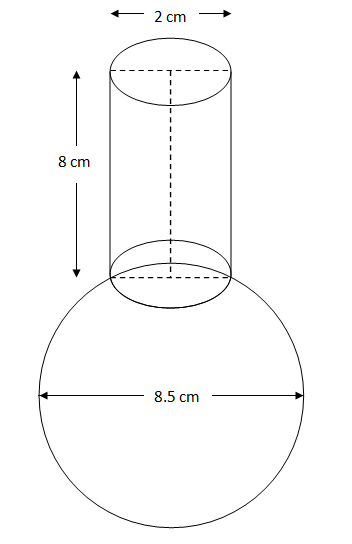

圆柱形颈的半径 = 2/2 = 1 cm

圆柱体的体积 = πr²h

= 3.14 × 1² × 8

= 25.12 cm³

球形部分的半径 = 8.5/2 = 4.25 cm

球体的体积 = 4/3 × πR³

= 4/3 × 3.14 × 4.25³

= 964.17625/3 cm³

容器的总体积 = 圆柱体体积 + 球体体积

= 25.12 + 964.17625/3

= (75.36 + 964.17625)/3

= 1039.54625/3

= 346.51 cm³

因此，这个孩子是错误的。正确的体积是346.51立方厘米。

练习13.3

除非另有说明，否则取 π = 22/7。

1. 一个半径为4.2厘米的金属球被熔化并重铸成一个半径为6厘米的圆柱体。求圆柱体的高度。

解决方案

金属球的体积 = 4/3 × πr³

= 4/3 × π × 4.2³

= 98.784π cm³

由于球体被重铸成圆柱体。因此，体积将保持不变。

圆柱体的体积 = 98.784π

πR²h = 98.784π

6² × h = 98.784

36h = 98.784

h = 2.744 cm

因此，圆柱体的高度是2.744厘米。

2. 将半径分别为6厘米、8厘米和10厘米的金属球熔化成一个单一的实心球体。求所得球体的半径。

解决方案

第一个球体的体积 = 4/3 × πr₁³

第二个球体的体积 = 4/3 × πr₂³

第三个球体的体积 = 4/3 × πr₃³

由于这三个球体都被重铸成一个。因此，组成球体的体积将等于组成球体体积的总和。

所得球体的体积 = 4/3 × πr₁³ + 4/3 × πr₂³ + 4/3 × πr₃³

4/3 × πR³ = 4/3 × π(r₁³ + r₂³ + r₃³)

R³ = 6³ + 8³ + 10³

R³ = 216 + 512 + 1000

R³ = 1728

R = 12 cm

因此，所得球体的半径为12厘米。

3. 一个深20米、直径7米的水井被挖开，挖出的土均匀地铺开形成一个22米×14米的平台。求平台的高度。

解决方案

圆柱形水井的体积 = πr²H

平台的体积 = l × b × h

由于从水井挖出的土被用来建造平台。因此，它们的体积将相等。

πr²H = l × b × h

22/7 × 7/2 × 7/2 × 20 = 22 × 14 × h

35 = 14h

5/2 = h

h = 2.5 m

因此，平台的高度是2.5米。

4. 一个直径3米的水井被挖深14米。挖出的土被均匀地铺开在水井周围，形成一个宽4米的圆形环形堤。求堤的高度。

解决方案

圆柱形水井的体积 = πr²H

堤的体积 = πR²h

由于从水井挖出的土被用来建造堤。因此，它们的体积将相等。

πr²H = πR²h

3/2 × 3/2 × 14 = 4/2 × 4/2 × h

126 = 16h

63/8 = h

h = 7.875 m

因此，堤的高度是7.875米。

5. 一个圆柱形容器，直径12厘米，高15厘米，装满了冰淇淋。冰淇淋将装入高12厘米、直径6厘米的圆锥体中，其顶部呈半球形。求可以装满冰淇淋的这种圆锥体的数量。

解决方案

圆柱形容器的体积 = πR²H

= π × 12/2 × 12/2 × 15

= 540π cm³

一个圆锥的体积 = 1/3 × πr²h

= 1/3 × π × 6/2 × 6/2 × 12

= 36π cm³

圆锥顶部的半球部分的体积 = 2/3 × πr³

= 2/3 × π × 6/2 × 6/2 × 6/2

= 18π cm³

每个冰淇淋圆锥中的冰淇淋体积 = 圆锥体积 + 半球体积

= 36π + 18π = 54π cm³

可以装满的冰淇淋圆锥数量 = 容器体积/每个冰淇淋圆锥中的冰淇淋体积

= 540π/54π

= 10

因此，容器中的冰淇淋可以装满10个冰淇淋圆锥。

6. 需要熔化多少枚直径1.75厘米、厚度2毫米的银币，才能铸成一个尺寸为5.5厘米×10厘米×3.5厘米的长方体？

解决方案

一枚银币的体积 = πr²h

= 22/7 × 1.75/2 × 1.75/2 × 0.2

= 0.48125 cm³

长方体的体积 = 5.5 × 10 × 3.5

= 192.5 cm³

所需的硬币数量 = 长方体体积/一枚硬币的体积

= 192.5/0.48125

= 400

因此，需要400枚银币才能铸成所需的长方体。

7. 一个圆柱形桶，高32厘米，底面半径18厘米，装满了沙子。将这个桶倒空在地上，形成一个圆锥形的沙堆。如果圆锥形沙堆的高度为24厘米，求沙堆的半径和斜高。

解决方案

沙子的体积 = 桶的体积 = πr²H

= π × 18² × 32

= 10368π cm³

圆锥形沙堆的体积 = 1/3 × πR²h

= 1/3 × π × R² × 24

= 8πR² cm³

由于桶里的沙子被用来制作圆锥形沙堆。因此，体积将保持不变。

10368π = 8πR²

1296 = R²

R = 36 cm

圆锥形沙堆的斜高 = √(h² + R²)

= √(24² + 36²)

= √(576 + 1296)

= √(1872)

= 12√13 cm

因此，圆锥形沙堆的半径为36厘米，斜高为12√13厘米。

8. 一条宽6米、深1.5米的运河中的水，以10公里/小时的速度流动。如果需要8厘米深的静止水，那么30分钟后它将灌溉多少面积？

解决方案

1小时内被水覆盖的运河长度 = 10公里 = 10000米

1分钟内被水覆盖的运河长度 = 10000/60米

30分钟内被水覆盖的运河长度 = 10000/60 × 30

= 5000米

被覆盖的运河宽度 = 6米

被覆盖的运河高度 = 1.5米

30分钟内通过运河的水的体积 = 5000 × 6 × 1.5

= 45000 m³

灌溉面积的体积 = 流经运河的水的体积

灌溉面积 × 水高 = 45000

A × 0.08 = 45000

A = 562500 m²

因此，在30分钟内，通过运河的水流将灌溉562500平方米的面积。

9. 一位农民将一条内径20厘米的管道连接到她田里的圆柱形水箱，该水箱直径10米，深2米。如果水流通过管道的速度为3公里/小时，那么水箱需要多长时间才能注满？

解决方案

1小时内通过管道的水流长度 = 3公里 = 3000米

1小时内通过管道的水流体积 = πr²H

= π × 0.2/2 × 0.2/2 × 3000

= 30π m³

1分钟内通过管道的水流体积 = 30π × 1/60 = 0.5π m³

注满水箱所需的水的体积 = 水箱体积 = πR²h

= π × 10/2 × 10/2 × 2

= 50π m³

注满水箱所需时间 = 水箱体积/1分钟内流过的水量

= 50π/0.5π

= 100分钟

因此，水流通过管道注满给定水箱需要100分钟。

练习13.4

除非另有说明，否则使用 π = 22/7。

1. 一个饮水杯是圆锥台形状，高14厘米。其两个圆形端部的直径分别为4厘米和2厘米。求杯子的容量。

解决方案

上半径 = 4/2 = 2 cm

下半径 = 2/2 = 1 cm

杯子的体积 = 圆锥台的体积

= 1/3 × π(r₁² + r₂² + r₁r₂)h

= 1/3 × 22/7 × (2² + 1² + 2(1))14

= 1/3 × 22/7 × (4 + 1 + 2)14

= 22/3 × 7 × 2

= 308/3 cm³

因此，杯子的容量 = 308/3 cm³

2. 一个圆锥台的斜高为4厘米，其圆形端部的周长（周长）分别为18厘米和6厘米。求圆锥台的侧面积。

解决方案

较大的圆形端的周长 = 2πr₁

18 = 2πr₁

r₁ = 9/π cm

较小圆形端的周长 = 2πr₂

6 = 2πr₂

r₂ = 3/π cm

圆锥台的侧面积 = πl(r₁ + r₂)

= π × 4 × (9/π + 3/π)

= π × 4 × 12/π

= 48 cm²

3. 一个土耳其人戴的帽子——菲斯帽，形状是圆锥台（见图13.24）。如果其开口侧半径为10厘米，顶端半径为4厘米，斜高为15厘米，求制作帽子所需的材料面积。

解决方案

闭合底部的半径 = r₁ = 4 cm

开口底部的半径 = r₂ = 10 cm

圆锥台的侧面积 = πl(r₁ + r₂)

= 22/7 × 15 × (4 + 10)

= 22/7 × 15 × 14

= 660 cm²

闭合底面积 = πr₁²

= 22/7 × 4²

= 352/7 cm²

制作帽子所需的材料面积 = 圆锥台侧面积 + 闭合底面积 = 660 + 352/7

= (4620 + 352)/7

= 4972/7 cm²

因此，制作帽子需要4972/7平方厘米的材料。

4. 一个顶部开口、由金属板制成的容器，呈圆锥台形状，高16厘米，其下端和上端的半径分别为8厘米和20厘米。求容器的容量（可装满的牛奶量）的成本，按每升20卢比计算。同时，求制作容器所需的金属板的成本，如果成本是每100平方厘米8卢比。（取π = 3.14）

解决方案

上端的半径 = r₁ = 20 cm

下端的半径 = r₂ = 8 cm

可完全装满容器的牛奶体积 = 圆锥台的体积

= 1/3 × πh(r₁² + r₂² + r₁r₂)

= 1/3 × 3.14 × 16 × (20² + 8² + 20(8))

= 1/3 × 3.14 × 16 × (624)

= 10449.92 cm³

= 10.44992 L

每升牛奶成本 = 20卢比

10.44992升牛奶的成本 = 20 × 10.44992 = 208.9984卢比或209卢比

容器的斜高 = l = √(h² + (r₁ - r₂)²)

= √(16² + (12)²)

= √(256 + 144)

= √(400)

= 20 cm

容器的侧面积 = πl(r₁ + r₂)

= 3.14 × 20 × (20 + 8)

= 62.8 × 28

= 1758.4 cm²

容器底面积 = πr₂²

= 3.14 × 8²

= 200.96 cm²

制作容器所需的金属面积 = 容器侧面积 + 底部面积

= 1758.4 + 200.96

= 1959.36 cm²

每100平方厘米金属板成本 = 8卢比

每平方厘米金属板成本 = 8/100 = 0.08卢比

1959.36平方厘米金属板的成本 = 0.08 × 1959.36

= 156.7488卢比或157卢比。

因此，装满容器所需的牛奶成本为209卢比，制作容器所需的金属板成本为157卢比（近似值）。

5. 一个高20厘米、竖直角为60°的金属直圆锥，在其高度中间处被一个与其底面平行的平面分成两部分。如果得到的圆锥台被拉成直径为1/16厘米的细线，求细线的长度。

解决方案

圆锥在其高度中间被分成两部分。因此，AO = DO = 20/2 = 10 cm

我们知道∠B和∠C为60°，这意味着

∠A = 180° - ∠B - ∠C （ABC的角度和为180°）

∠A = 180° - 60° - 60°

∠A = 60°

ABC构成一个等边三角形。因此，垂直线AD将平分∠A。

∠BAD = ∠CAD = 30°

在? AEO中

tan 30° = EO/AO

1/√3 = EO/10

EO = 10/√3 cm

在? ABD中

tan 30° = BD/AD

1/√3 = BD/20

BD = 20/√3 cm

圆锥台较大的圆形端的半径 = r₁ = 20/√3 cm

圆锥台较小的圆形端的半径 = r₂ = 10/√3 cm

圆锥台的体积 = 1/3 × πh(r₁² + r₂² + r₁r₂)

= 1/3 × π × 10((20/√3)² + (10/√3)² (20/√3) (10/√3))

= 1/3 × π × 10(400/3 + 100/3 + 200/3)

= 1/3 × π × 10(700/3)

= 7000π/9 cm³

由于圆锥台被拉成了细线。因此，它们的体积将相等。

圆柱形细线的体积 = 圆锥台的体积

πr²H = 7000π/9

1/32 × 1/32 × H = 7000/9

H = 7000/9 × 1024

H = 796444.44 cm 或 7964.44 m

因此，细线的长度是7964.44米。

练习13.5（可选）

1. 一根直径为3毫米的铜丝，缠绕在一个长12厘米、直径10厘米的圆柱体上，以覆盖圆柱体的曲面。求铜丝的长度和质量，假设铜的密度为每立方厘米8.88克。

解决方案

圆柱体的半径 = R = 10/2 = 5 cm

完成圆柱体一圈所需的铜丝长度 = 2πR

= 2 × 22/7 × 5 = 31.42 cm

铜丝的直径 = 3毫米 = 0.3厘米

覆盖圆柱体0.3厘米高度所需的铜丝圈数 = 1

覆盖圆柱体1厘米高度所需的铜丝圈数 = 1/0.3 = 10/3

覆盖圆柱体12厘米高度所需的铜丝圈数 = 12 × 10/3 = 40

覆盖圆柱体曲面所需的铜丝长度 = 一圈铜丝长度 × 40

= 31.42 × 40 = 1256 cm

铜丝的体积 = πr²H

= 22/7 × 0.3/2 × 0.3/2 × 1256

= 88.81 cm³

铜丝的质量 = 体积 × 密度

= 88.81 × 8.88

= 788.63克

2. 一个直角三角形，其边长为3厘米和4厘米（斜边除外），使其绕其斜边旋转。求所得双圆锥的体积和表面积。（选择合适的π值。）

解决方案

根据ABC中的勾股定理，我们得到

BC² = AB² + AC²

BC² = 3² + 4²

BC² = 9 + 16

BC² = 25

BC = 5 cm

在? ABC 和 ? AOC 中

∠BAC = ∠AOC （直角）

∠ACB = ∠ACO （公共角）

因此，根据AA相似准则 ? ABC ~ ? AOC。

这意味着

AB/AO = BC/AC （相似三角形的对应边）

AO = AB × AC/BC

AO = 3 × 4/5 = 12/5 cm

类似地，

BO = AB²/BC

BO = 3²/5 = 9/5 cm

CO = BC - BO = 5 - 9/5 = 16/5 cm

两个圆锥体的半径 = AO = DO = 12/5 cm

较小圆锥体的体积 = 1/3 × πr²h

= 1/3 × 3.14 × 12/5 × 12/5 × 9/5

= 10.85 cm³

较大圆锥体的体积 = 1/3 × πr²H

= 1/3 × 3.14 × 12/5 × 12/5 × 16/5

= 19.29 cm³

形成的双圆锥体的体积 = 10.85 + 19.29

= 30.14 cm³

较小圆锥体的侧面积 = πrl

= 3.14 × 12/5 × 3

= 22.6 cm²

较大圆锥体的侧面积 = πrL

= 3.14 × 12/5 × 4

= 30.14 cm²

形成的双圆锥体的表面积 = 较小圆锥侧面积 + 较大圆锥侧面积

= 22.6 + 30.14 = 52.74 cm²

3. 一个水箱，内部尺寸为150厘米×120厘米×110厘米，里面有129600立方厘米的水。将多孔砖放入水中，直到水箱满溢。每块砖吸收其自身体积的十七分之一的水。在不溢出的情况下，最多可以放入多少块砖，每块砖的尺寸为22.5厘米×7.5厘米×6.5厘米？

解决方案

水箱完全排空时的体积 = 150 × 120 × 110

= 1980000 cm³

注满水后的剩余体积 = 1980000 - 129600 = 1850400 cm³

一块砖的体积 = 22.5 × 7.5 × 6.5

= 1096.875 cm³

一块砖吸收的水的体积 = 1096.875/17 cm³

所需砖块数量 = (水箱剩余体积 + 一块砖吸收的水的体积)/ 一块砖的体积

= (1850400 + 1096.875/17)/1096.875

? 1792

因此，最多可以向水箱中放入1792块砖而不溢出。

4. 在给定月份的两个星期中，一个河流流域的降雨量为10厘米。如果流域面积为7280平方公里，则表明总降雨量约等于三个河流的正常水量增加，每个河流长1072公里，宽75米，深3米。

解决方案

一条河的水量 = 1072 × 1000 × 75 × 3

= 241200000 m³

三条河的水量 = 241200000 × 3 = 723600000 m³

降雨量的高度 = 10厘米 = 0.1米

由于降雨而导致河流流域的水量 = 河流流域的表面积 × 降雨高度

= (7280 × 1000000) × 0.1

= 728000000 m³

三条河流正常水量的增加量为7.236 × 10⁸立方米，而河流流域因降雨而水量为7.28 × 10⁸立方米。因此，它们近似相等。

因此，证明完毕。

5. 一个用锡板制成的油漏斗，由一个10厘米长的圆柱形部分和一个圆锥台组成。如果总高度为22厘米，圆柱形部分的直径为8厘米，漏斗顶部的直径为18厘米，求制作漏斗所需的锡板面积（见图13.25）。

解决方案

圆锥台较大端的半径 = r₁ = 18/2 = 9 cm

圆锥台较小端的半径 = r₂ = 8/2 = 4 cm

漏斗的圆锥台部分的高度 = H = 22 - 10 = 12 cm

圆锥台的斜高 l = √((r₁ - r₂)² + H²)

= √((9 - 4)² + 12²)

= √(5² + 144)

= √(25 + 144)

= √169

= 13 cm

圆锥台的侧面积 = π(r₁ + r₂)l

= 22/7 × (9 + 4) × 13

= 22/7 × 13 × 13

= 3718/7 cm²

圆柱形部分的半径 = r = 8/2 = 4 cm

圆柱形部分的侧面积 = 2πrh

= 2 × 22/7 × 4 × 10

= 1760/7 cm²

制作漏斗所需的锡板面积 = 圆锥台侧面积 + 圆柱体侧面积

= 3718/7 + 1760/7

= 5478/7

= 782.57 cm²

因此，制作漏斗将需要782.57平方厘米的锡板。

6. 根据第13.5节中给出的符号，推导圆锥台侧面积和总表面积的公式。

解决方案

设有一个圆锥ABC，由平行于底边BC的线PQ分割成圆锥台PBCQ，PQ垂直于圆锥的垂直线AD于点O。

考虑绘制的图形。

在? AOP 和 ? ADB 中

∠AOP = ∠ADB （直角）

∠PAO = ∠BAD （公共角）

因此，根据AA相似准则 ? AOP ~ ? ADB。

这意味着：

PO/BD = AO/AD = AP/AB （相似三角形的对应边）

r₂/r₁ = (H - h)/H = (L - l)/L

r₂/r₁ = 1 - h/H = 1 - l/L

因此，r₂/r₁ = 1 - l/L

l/L = 1 - r₂/r₁ = (r₁ - r₂/r₁)

L = lr₁/(r₁ - r₂)

圆锥ABC的侧面积 = πr₁L

圆锥APQ的侧面积 = πr₂(L - l)

圆锥台PBCQ的侧面积 = πr₁L - πr₂(L - l)

= πr₁ × (lr₁/(r₁ - r₂)) - πr₂ × (lr₁/(r₁ - r₂) - l)

= πr₁²l/(r₁ - r₂) - πr₂ × (lr₁ - lr₁ + lr₂)/(r₁ - r₂)

= πr₁²l/(r₁ - r₂) - πr₂²l/(r₁ - r₂)

= πl × (r₁² - r₂²)/(r₁ - r₂)

= πl × (r₁ - r₂)(r₁ + r₂)/(r₁ - r₂)

= π(r₁ + r₂)l

圆锥台PBCQ的总表面积 = 侧面积 + 上底面积 + 下底面积

= π(r₁ + r₂)l + πr₂² + πr₁²

= π((r₁ + r₂)l + r₁² + r₂²)

因此，推导出了所需的公式。

7. 根据第13.5节中给出的符号，推导圆锥台体积的公式。

解决方案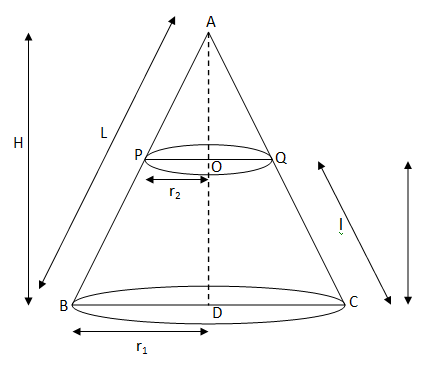

设有一个圆锥ABC，由平行于底边BC的线PQ分割成圆锥台PBCQ，PQ垂直于圆锥的垂直线AD于点O。

考虑绘制的图形。

在? AOP 和 ? ADB 中

∠AOP = ∠ADB （直角）

∠PAO = ∠BAD （公共角）

因此，根据AA相似准则 ? AOP ~ ? ADB。

这意味着：

PO/BD = AO/AD = AP/AB （相似三角形的对应边）

r₂/r₁ = (H - h)/H = (L - l)/L

r₂/r₁ = 1 - h/H = 1 - l/L

因此，r₂/r₁ = 1 - h/H

h/H = 1 - r₂/r₁ = (r₁ - r₂/r₁)

H = hr₁/(r₁ - r₂)

圆锥ABC的体积 = 1/3 × πr₁²H

圆锥APQ的体积 = 1/3 × πr₂²(H - h)

圆锥台PBCQ的体积 = ABC的体积 - APQ的体积

= 1/3 × πr₁²H - 1/3 × πr₂²(H - h)

= 1/3 × (πr₁²hr₁/(r₁ - r₂) - πr₂²(hr₁/(r₁ - r₂) - h))

= π/3 × (hr₁³/(r₁ - r₂) - r₂²(hr₁ - hr₁ + hr₂)/(r₁ - r₂))

= π/3 × (hr₁³/(r₁ - r₂) - hr₂³/(r₁ - r₂))

= πh/3 × (r₁³ - r₂³)/(r₁ - r₂)

= πh/3 × (r₁ - r₂)(r₁² + r₂² + r₁r₂)/(r₁ - r₂)

= 1/3 × πh(r₁² + r₂² + r₁r₂)

因此，推导出了所需的公式。