NCERT 10年级数学第7章：坐标几何

练习 7.1

1. 求下列两点间的距离

1. (2, 3), (4, 1)
2. (- 5, 7), (- 1, 3)
3. (a, b), (- a, - b)

解决方案

I. 令 (2, 3) = (x₁, y₁) 且 (4, 1) = (x₂, y₂)。

两点间的距离

因此，给定两点间的距离为 2√2 单位。

II. 令 (-5, 7) = (x₁, y₁) 且 (-1, 3) = (x₂, y₂)。

两点间的距离

因此，给定两点间的距离为 4√2 单位。

III. 令 (a, b) = (x₁, y₁) 且 (-a, -b) = (x₂, y₂)。

两点间的距离

因此，给定两点间的距离为 2√(a² + b²) 单位。

2. 求点 (0, 0) 和 (36, 15) 之间的距离。现在你能求出第 7.2 节中讨论的 A 和 B 两镇之间的距离吗？

解决方案

令 (0, 0) = (x₁, y₁) 且 (36, 15) = (x₂, y₂)。

两点间的距离

(第 7.2 节中的两镇 A 和 B 具有与问题第一部分相同的坐标，因此它们之间的距离为 39 公里。)

3. 判断点 (1, 5), (2, 3) 和 (- 2, - 11) 是否共线。

解决方案

令给定的坐标 (1, 5), (2, 3) 和 (- 2, - 11) 分别为 A, B 和 C。

如果这些点共线，则较短距离之和等于最长距离。

A 和 B 之间的距离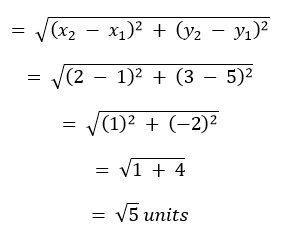

B 和 C 之间的距离

A 和 C 之间的距离

较短距离之和 = √5 + √212 = √217 单位

因为 √217 ? √265，所以给定的点不共线。

4. 检查 (5, - 2), (6, 4) 和 (7, - 2) 是否为等腰三角形的顶点。

解决方案

令给定的坐标 (5,-2), (6, 4) 和 (7,-2) 分别为 A, B 和 C。

如果这些点构成一个等腰三角形，那么两点对之间必须有两个距离相等。

因为 AB = BC。所以，给定的点将构成一个等腰三角形。

5. 在教室里，4 个朋友按图 7.8 所示的点 A、B、C 和 D 入座。Champ 和 Chameli 走进教室，观察了几分钟后，Champ 问 Chameli：“你不觉得 ABCD 是个正方形吗？” Chameli 不同意。使用距离公式，找出谁是正确的。

解决方案

如果 ABCD 构成一个正方形，那么所有边都必须相等，即 AB = BC = CD = AD，并且对角线 AC 和 BD 也必须相等。

因为 AB = BC = CD = AD。所以，ABCD 构成一个四边形，所有边都相等，即菱形或正方形。我们将计算对角线的长度来找出 ABCD 是菱形还是正方形。

因为 ABCD 的对角线相等。所以，该四边形是正方形。

因此，Champ 是正确的。

6. 如果有，请命名由下列点形成的四边形的类型，并给出原因

1. (- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
2. (-3, 5), (3, 1), (0, 3), (-1, - 4)
3. (4, 5), (7, 6), (4, 3), (1, 2)

解决方案

I. 令给定的坐标 (-1, -2), (1, 0), (-1, 2) 和 (-3, 0) 分别为 A, B, C 和 D。

因为 AB = BC = CD = AD。所以，ABCD 构成一个四边形，所有边都相等，即菱形或正方形。我们将计算对角线的长度来找出 ABCD 是菱形还是正方形。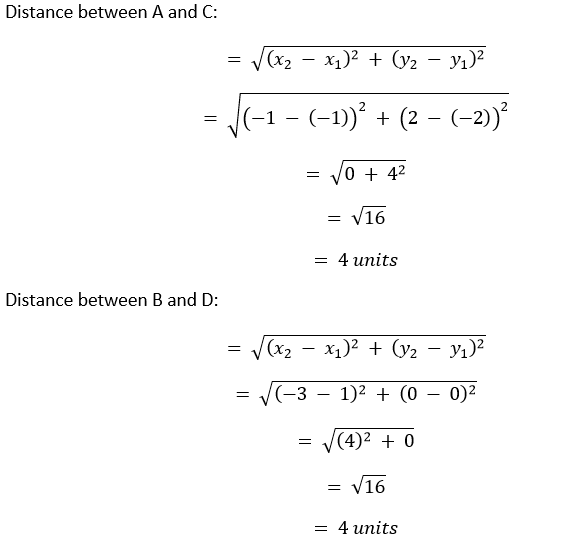

因此，给定的点构成一个正方形。

II. 令给定的坐标 (-3, 5), (3, 1), (0, 3) 和 (-1, -4) 分别为 A, B, C 和 D。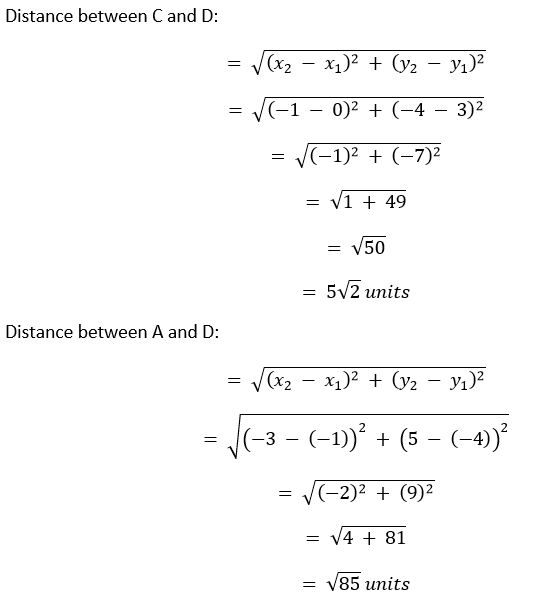

给定的点不构成四边形。

III. 令给定的坐标 (4, 5), (7, 6), (4, 3) 和 (1, 2) 分别为 A, B, C 和 D。

因为 AB = CD 且 BC = AD。所以，ABCD 构成一个四边形，对边相等，即平行四边形或矩形。我们将计算对角线的长度来找出 ABCD 是平行四边形还是矩形。

对角线不相等。

因此，给定的点构成一个平行四边形。

7. 求 x 轴上与点 (2, -5) 和 (-2, 9) 等距的点。

解决方案

所求点位于 x 轴上，这意味着其 y 坐标为 0。然后，令所求点为 (x, 0)。

根据问题

点 (2, -5) 与 (x, 0) 之间的距离 = 点 (x, 0) 与 (-2, 9) 之间的距离

因此，所求点为 (-7, 0)。

8. 求 y 的值，使得点 P(2, - 3) 和 Q(10, y) 之间的距离为 10 单位。

解决方案

已知

P 和 Q 之间的距离 = 10 单位

9. 如果 Q(0, 1) 与 P(5, -3) 和 R(x, 6) 等距，则求 x 的值。还求 QR 和 PR 的距离。

解决方案

根据问题，我们有

Q 和 P 之间的距离 = Q 和 R 之间的距离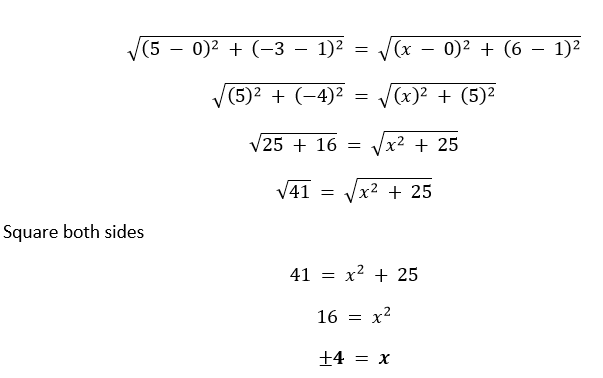

因此，x 是 4 或 -4。

情况 I：当 x = 4 时。

情况 II：当 x = -4 时。

因此，x = �4 且 QR 和 PR 的距离分别为 √41 单位和 √82 单位，或者分别为 √41 单位和 9√2 单位。

10. 求 x 和 y 之间的关系，使得点 (x, y) 与点 (3, 6) 和 (- 3, 4) 等距。

解决方案

根据问题，我们有

点 (3, 6) 与 (x, y) 之间的距离 = 点 (-3, 4) 与 (x, y) 之间的距离

因此，3x - y = 5 是所需的关系。

练习 7.2

1. 求分点 (-1, 7) 和 (4, -3) 所连线段的比为 2 : 3 的点的坐标。

解决方案

令给定的点为 A (-1, 7) 和 C (4, -3)，它们的连线被点 B (x, y) 分成比。

B 的坐标将是

因此，所需点为 (1, 3)。

2. 求分点 (4, -1) 和 (-2, -3) 所连线段的三等分点的坐标。

解决方案

令点为 A (4, -1) 和 D (-2, -3)，它们被两个点 B (x, y) 和 C (X, Y) 三等分。

由于线段 AD 被三等分，因此 AD 被 B 按 1 : 2 的比例，被 C 按 2 : 1 的比例分。

因此，

因此，所需点为 (2, -5/3) 和 (0, -7/3)。

3. 为了进行运动会活动，在你的长方形学校操场 ABCD 中，每隔 1 米画了线。按照图 7.12 所示，在 AD 上每隔 1 米放置了 100 盆花。Niharika 在第 2 条线上跑了 AD 距离的 1/4，并插了一面绿旗。Preet 在第 8 条线上跑了 AD 距离的 1/5，并插了一面红旗。两面旗子之间的距离是多少？如果 Rashmi 要在两面旗子所连线段的正中间插一面蓝旗，她应该把旗子插在哪里？

解决方案

AD 的总距离 = 100 米

Niharika 在第 2 条线上跑步，并将旗子插在 AD 距离的 1/4 处。因此，绿旗的位置 = (2, 1/4 × 100) = (2, 25)

Preet 在第 8 条线上跑步，并将旗子插在 AD 距离的 1/5 处。因此，红旗的位置 = (8, 1/5 × 100) = (8, 20)

两面旗子之间的距离

因此，红旗和绿旗之间的距离为 √61 米。

蓝旗需要插在连接红旗和绿旗的线段的中点。那么，蓝旗的坐标是

因此，Rashmi 需要在第 5 条线上将蓝旗插在 45/2 米处。

4. 求线段 (- 3, 10) 和 (6, - 8) 被 (- 1, 6) 分成的比例。

解决方案

令给定的点为 A (-3, 10) 和 C (6, -8)，被点 B (-1, 6) 分割。

根据分点公式

因此，所需比例为 m : n = 2 : 7。

5. 求线段 A(1, - 5) 和 B(- 4, 5) 被 x 轴分成的比例。还求分点的坐标。

解决方案

因为给定的线段被 x 轴分成，所以分点的坐标将是 (x, 0)。

根据分点公式，我们可以说

因此，线段 AB 按 1 : 1 的比例被分割。

这意味着 x 轴上的分点是 AB 的中点。

因此，

因此，所需点为 (-3/2, 0)。

6. 如果 (1, 2), (4, y), (x, 6) 和 (3, 5) 是按顺序排列的平行四边形的顶点，则求 x 和 y。

解决方案

令给定的点为 A (1, 2), B (4, y), C (x, 6) 和 D (3, 5)。

因为 ABCD 构成一个平行四边形，所以对角线 AC 和 BD 将在 (X, Y) 处相互平分。因此，

因此，x = 6 且 y = 3。

7. 求一个点 A 的坐标，其中 AB 是圆的直径，该圆的圆心是 (2, - 3) 且 B 是 (1, 4)。

解决方案

令 A 为 (x₁, y₁)。

圆心是直径的中点。因此，(2, -3) 是 AB 的中点。这意味着

因此，点 A 将是 (3, -10)。

8. 如果 A 和 B 分别是 (- 2, - 2) 和 (2, - 4)，则求 P 的坐标，使得 AP = 3/7 AB 且 P 位于线段 AB 上。

解决方案

因此，点 P 将 AB 按 3 : 4 的比例分。那么，P 的坐标将是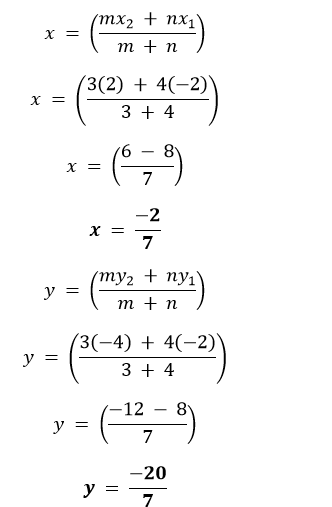

因此，P 的坐标是 (-2/7, -20/7)。

9. 求将线段 A(- 2, 2) 和 B(2, 8) 分成四等份的点的坐标。

解决方案

令 P (a, b), Q (x, y) 和 R (α, β) 为三个所需点。

已知 P, Q 和 R 将线段 AB 分成四等份。这意味着 Q 将是 AB 的中点，P 将是 AQ 的中点，而 R 将是 BQ 的中点。

Q 的坐标

因此，Q 是 (0, 5)。

P 的坐标

因此，P 是 (-1, 7/2)。

R 的坐标

因此，R 是 (1, 13/2)。

因此，所需点为 (-1, 7/2), (0, 5), 和 (1, 13/2)。

10. 求一个菱形的面积，其顶点按顺序为 (3, 0), (4, 5), (- 1, 4) 和 (- 2, - 1)。[提示：菱形面积 = ½(对角线乘积)]

解决方案

令菱形的顶点为 A (3, 0), B (4, 5), C (-1, 4) 和 D (-2, -1)。

给定菱形的面积 = ½ × AC × BD

= ½ × 4√2 × 6√2

= ½ × 48

= 24 平方单位。

因此，给定菱形的面积为 24 平方单位。

练习 7.3

1. 求顶点为下列的三角形的面积

1. (2, 3), (-1, 0), (2, - 4)
2. (-5, -1), (3, -5), (5, 2)

解决方案

I. 给定三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[2(0 - (-4)) - 1(-4 - 3) + 2(3 - 0)]

= ½[2(4) - 1(-7) + 2(3)]

= ½[8 + 7 + 6]

= ½[21]

= 21/2 = 10.5 平方单位

II. 给定三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[-5(-5 - 2) + 3(2 - (-1)) + 5(-1 - (-5))]

= ½[-5(-7) + 3(3) + 5(4)]

= ½[35 + 9 + 20]

= ½[64]

= 64/2 = 32 平方单位

1. (7, -2), (5, 1), (3, k)
2. (8, 1), (k, - 4), (2, -5)。

解决方案

I. 如果点共线，则由它们形成的三角形的面积将为 0。

由点形成的三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

0 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

0 = [7(1 - k) + 5(k - (-2)) + 3(-2 - 1)]

0 = [7 - 7k + 5(k + 2) + 3(-3)]

0 = [7 - 7k + 5k + 10 - 9]

0 = [- 2k + 8]

-8 = -2k

k = 4

II. 如果点共线，则由它们形成的三角形的面积将为 0。

由点形成的三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

0 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

0 = [8(-4 - (-5)) + k(-5 - 1) + 2(1 - (-4))]

0 = [8(-4 + 5) + k(-6) + 2(5)]

0 = [8(1) - 6k + 10]

0 = [8 - 6k + 10]

0 = - 6k + 18

-18 = -6k

k = 3

3. 求由顶点为 (0, -1), (2, 1) 和 (0, 3) 的三角形各边中点连接而成的三角形的面积。求此面积与给定三角形面积之比。

解决方案

令给定的点为 A (0, -1), B (2, 1) 和 C (0, 3)，D, E 和 F 分别为 AB, BC, 和 AC 的中点。

D 的坐标

D 是 (1, 0)。

E 的坐标

E 是 (1, 2)。

F 的坐标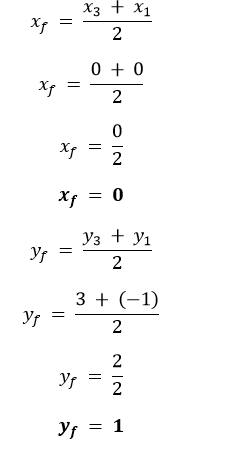

F 是 (0, 1)。

DEF 的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[1(2 - 1) + 1(1 - 0) + 0(0 - 2)]

= ½[1(1) + 1(1) + 0]

= ½[1 + 1 + 0]

= ½[2]

= 1 平方单位

ABC 的面积 =

= ½[0(1 - 3) + 2(3 + 1) + 0(-1 - 1)]

= ½[0 + 2(4) + 0]

= ½[0 + 8 + 0]

= ½[8]

= 4 平方单位

DEF 和 ABC 的面积之比 = DEF 的面积/ ABC 的面积

= ¼ = 1 : 4

因此，由给定三角形的中点连接而成的三角形的面积为 1 平方单位，两个三角形的面积之比为 1 : 4。

4. 求按顺序排列的顶点为 (- 4, - 2), (- 3, - 5), (3, - 2) 和 (2, 3) 的四边形的面积。

解决方案

令给定四边形的顶点为 A (-4, -2), B(-3, -5), C(3, -2), 和 D(2, 3)。

我们可以将 ABCD 分成两个三角形 ABC 和 ADC，并求它们的面积之和以求 ABCD 的面积。

三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

ABC 的面积 = ½[-4(-5 - (-2)) - 3(-2 - (-2)) + 3(-2 - (-5))]

= ½[-4(-5 + 2) - 3(-2 + 2) + 3(3)]

= ½[-4(-3) - 3(0) + 9]

= ½[12 + 9]

= ½[21]

= 21/2 = 10.5 平方单位

ADC 的面积 = ½[-4(-2 - 3) + 3(3 - (-2)) + 2(-2 - (-2))]

= ½[-4(-5) + 3(3 + 2) + 2(-2 + 2)]

= ½[20 + 3(5) + 2(0)]

= ½[20 + 15]

= ½[35]

= 35/2 = 17.5 平方单位

ABCD 的面积 = 10.5 + 17.5 = 28 平方单位

因此，给定四边形的面积为 28 平方单位。

5. 你在九年级（第 9 章，例 3）学过，三角形的中线将其分成面积相等的两个三角形。对于顶点为 A(4, - 6), B(3, -2) 和 C(5, 2) 的 ∆ ABC，验证此结果。

解决方案

令 AD 为三角形 ABC 的中线。

D 将是 BC 的中点。因此，D 的坐标将是

D 是 (4, 0)。

三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

ADB 三角形的面积 = ½[4(0 - (-2)) + 4(-2 - (-6)) + 3(-6 - 0)]

= ½[4(2) + 4(-2 + 6) + 3(-6)]

= ½[8 + 4(4) - 18]

= ½[8 + 16 - 18]

= ½[6]

= 6/2 = 3 平方单位

ADC 三角形的面积 = ½[4(0 - 2) + 4(2 - (-6)) + 3(-6 - 0)]

= ½[4(-2) + 4(2 + 6) + 3(-6)]

= ½[-8 + 4(8) - 18]

= ½[-8 + 32 - 18]

= ½[6]

= 6/2 = 3 平方单位

因此，证明了三角形的中线将其分成面积相等的两个三角形。

练习 7.4 (可选)

1. 确定直线 2x + y - 4 = 0 分割点 A(2, - 2) 和 B(3, 7) 所连线段的比例。

解决方案

令 AB 被 2x + y - 4 = 0 分割的比例为 k : 1。

交点的坐标可以得到为

因为交点也将位于 2x + y - 4 = 0 上。因此，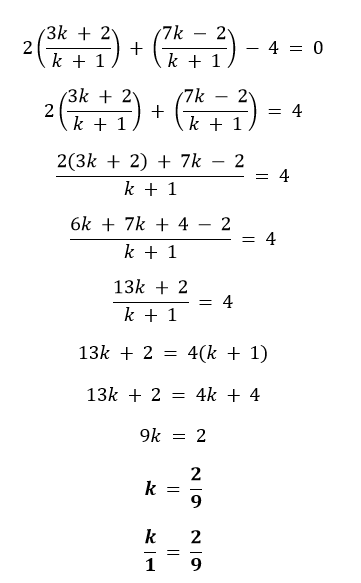

因此，AB 被 2x + y - 4 = 0 分割的比例为 2 : 9。

2. 如果点 (x, y), (1, 2) 和 (7, 0) 共线，则求 x 和 y 之间的关系。

解决方案

因为已知这些点共线。因此，由它们形成的三角形的面积将为 0。

三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

0 = ½[x(2 - 0) + 1(0 - y) + 7(y - 2)]

0 = ½[x(2) + 1(-y) + 7y - 14]

0 = ½[2x - y + 7y - 14]

0 = ½[2x + 6y - 14]

2x + 6y - 14 = 0

2(x + 3y - 7) = 0

x + 3y - 7 = 0

因此，x + 3y - 7 = 0 是所需的关系。

3. 求通过点 (6, - 6), (3, - 7) 和 (3, 3) 的圆的圆心。

解决方案

令圆心为 O (x, y) 且它经过的三点为 A (6, -6), B (3, -7), 和 C (3, 3)。

因为 OA, OB 和 OC 都是同一个圆的半径。因此，

OA = OB = OC

从方程 (II) 开始，我们得到

x - 3y = 9

x = 9 + 3y

将 x = 9 + 3y 代入方程 (I)，

3x + y = 7

3(9 + 3y) + y = 7

27 + 9y + y = 7

10y = -20

y = -2

x = 9 + 3y = 9 + 3(-2) = 9 - 6

x = 3

因此，圆心位于 (3, -2)。

4. 正方形的两个相对顶点为 (-1, 2) 和 (3, 2)。求另外两个顶点的坐标。

解决方案

令正方形为 ABCD，其中 A (-1, 2) 和 C (3, 2)。

AB = BC，因为 ABCD 是正方形。

AD = DC，因为 ABCD 是正方形。

通过在 ABC 中应用勾股定理，我们得到

AB² + BC² = AC²

(x_B - (-1))² + (y_B - 2)² + (3 - x_B)² + (2 - y_B)² = (3 - (-1))² + (2 - 2)²

(x_B + 1)² + (y_B - 2)² + (3 - x_B)² + (2 - y_B)² = (3 + 1)² + (0)²

(1 + 1)² + (y_B - 2)² + (3 - 1)² + (2 - y_B)² = (4)² + 0

(2)² + (y_B - 2)² + (2)² + (2 - y_B)² = 16

4 + (y_B - 2)² + 4 + (2 - y_B)² = 16

(y_B - 2)² + (-(y_B - 2))² = 8

(y_B - 2)² + (y_B - 2)² = 8

2(y_B - 2)² = 8

(y_B - 2)² = 4

y_B - 2 = �2

y_B = 4 或 y_B = 0

类似地，我们可以发现 y_D = 0 或 4。

由于 B 和 D 具有相同的 x 坐标，因此它们的 y 坐标不能相同，因为这将意味着正方形的点 B 和 D 重合，这是不可能的。

因此，B 和 D 分别是 (1, 4) 和 (1, 0)，或者 B 和 D 分别是 (1, 0) 和 (1, 4)。

因此，给定正方形的另外两个顶点是 (1, 4) 和 (1, 0)。

5. Krishinagar 一所中学的十年级学生被分配了一块矩形土地用于园艺活动。每隔 1 米在边界上种植了凤凰木幼苗。图 7.14 所示的场地内有一个三角形草坪。学生将在地块的剩余区域播种观赏植物的种子。

1. 以 A 为原点，求三角形顶点的坐标。
2. 如果 C 为原点，∆ PQR 的顶点坐标是多少？

还计算这些情况下的三角形面积。你有什么发现？

解决方案

I. 从图中可以看出 P = (4, 6), Q = (3, 2) 和 R = (6, 5)。

以 A 为原点的 PQR 面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[4(2 - 5) + 3(5 - 6) + 6(6 - 2)]

= ½[4(-3) + 3(-1) + 6(4)]

= ½[-12 - 3 + 24]

= ½[9]

= 9/2 = 4.5 m²

II. 从图中可以看出 P = (12, 2), Q = (13, 6) 和 R = (10, 3)。

以 C 为原点的 PQR 面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[12(6 - 3) + 13(3 - 2) + 10(2 - 6)]

= ½[12(3) + 13(1) + 10(-4)]

= ½[36 + 13 - 40]

= ½[9]

= 9/2 = 4.5 m²

观察：无论原点如何，三角形的面积都保持不变。

6. ∆ABC 的顶点为 A(4, 6), B(1, 5) 和 C(7, 2)。画一条线与边 AB 和 AC 分别相交于 D 和 E，使得 AD/AB = AE/AC = ¼。计算 ∆ ADE 的面积，并将其与 ∆ABC 的面积进行比较。(回忆定理 6.2 和定理 6.6)。

[供参考
定理 6.2：如果一条直线按相同比例分割三角形的两条边，则该直线平行于第三边。

定理 6.6：两个相似三角形的面积之比等于其对应边之比的平方。]

解决方案

D 和 E 将 AB 和 AC 按 1 : 3 的比例分。

D 的坐标

D 是 (13/4, 23/4)。

E 的坐标

E 是 (19/4, 5)。

ADE 三角形的面积 = ½[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

= ½[4(23/4 - 5) + 13/4(5 - 6) + 19/4(6 - 23/4)]

= ½[4(23/4 - 20/4) + 13/4(-1) + 19/4(24/4 - 23/4)]

= ½[4(3/4) - 13/4 + 19/4(1/4)]

= ½[3 - 13/4 + 19/16]

= ½[48/16 - 52/16 + 19/16]

= ½[15/16]

= 15/32 平方单位

ABC 三角形的面积 = ½[4(5 - 2) + 1(2 - 6) + 7(6 - 5)]

= ½[4(3) + 1(-4) + 7(1)]

= ½[12 - 4 + 7]

= ½[15]

= 15/2 平方单位

两个三角形面积之比 = ADE 面积/ ABC 面积 = (15/32)?(15/2)

= 1 : 16

因此，ADE 与 ABC 的面积之比为 1 : 16。

7. 令 ∆ABC 的顶点为 A (4, 2), B(6, 5) 和 C(1, 4)。

1. 从 A 点画出的中线与 BC 相交于 D。求点 D 的坐标。
2. 求 AD 上点 P 的坐标，使得 AP : PD = 2 : 1
3. 求中线 BE 和 CF 上的点 Q 和 R 的坐标，使得 BQ : QE = 2 : 1 且 CR : RF = 2 : 1。
4. 你有什么发现？

[注意：所有三条中线都经过的点称为重心，该点将每条中线按 2 : 1 的比例分割。]

解决方案

I. D 将是 BC 的中点，因为 AD 是中线。因此，D 的坐标是

D 是 (7/2, 9/2)。

II. P 的坐标是

P 是 (11/3, 11/3)。

III. E 将是 AC 的中点，因为 BE 是中线。因此，D 的坐标是

E 是 (5/2, 3)。

现在，Q 的坐标

Q 是 (11/3, 11/3)。

类似地，我们也可以发现 R 也是 (11/3, 11/3)。

IV. P, Q 和 R 重合，因为它们是所有三条中线的交点，称为三角形的重心。

V. 对于给定的三角形，重心坐标可以计算为

8. ABCD 是由点 A(-1, -1), B(- 1, 4), C(5, 4) 和 D(5, - 1) 形成的矩形。P, Q, R 和 S 分别是 AB, BC, CD 和 DA 的中点。四边形 PQRS 是正方形吗？矩形？还是菱形？证明你的答案。

解决方案

因为 P 是 AB 的中点。因此，它的坐标是

P 是 (-1, 3/2)。

类似地，我们可以发现

Q 是 (2, 4)

R 是 (5, 3/2)

以及 S 是 (2, -1)。

P 和 Q 之间的距离

类似地，我们可以发现

这意味着所有边都相等，因此 PQRS 是菱形或正方形。

因此，我们可以得出结论 PQRS 是一个所有边相等但对角线不相等的四边形。

因此，PQRS 是一个菱形。