10年级数学第九章：三角学在某些方面的应用 解决方案

练习 9.1

1. 一个马戏团的艺术家正在爬一根长20米的绳子，这根绳子被拉紧并从一根垂直杆的顶部固定到地面。如果绳子与地面形成的夹角为30°，则求出杆的高度（参见图9.11）。

解决方案

可以看出，ABC是一个直角三角形，AC是斜边。因此，

sin C = AB/AC

sin 30° = AB/20

1/2 = AB/20

AB = 20/2 = 10米

因此，垂直杆的高度为10米。

2. 一棵树因风暴而折断，折断的部分弯曲，使得树顶接触地面，与地面形成30°角。树脚到树顶接触地点的距离为8米。求出树的高度。

解决方案

设树剩余的垂直部分为AB，倒下的部分为AC。

可以看出，ABC构成一个直角三角形，AC是它的斜边。

因此，

cos C = BC/AC

cos 30° = 8/AC

√3/2 = 8/AC

AC = 16/√3米

tan C = AB/BC

1/√3 = AB/8

AB = 8/√3米

树的高度 = AB + AC = 8/√3米 + 16/√3米 = 24/√3米

有理化，

24/√3 × √3/√3 = 8√3米

因此，树的高度为8√3米。

3. 一位承包商计划为公园里的孩子们安装两个滑梯。对于5岁以下的孩子，她倾向于建造一个高度为1.5米、与地面成30°角的滑梯；而对于年龄较大的孩子，她想要建造一个陡峭的滑梯，高度为3米，并与地面成60°角。两种情况下滑梯的长度应为多少？

解决方案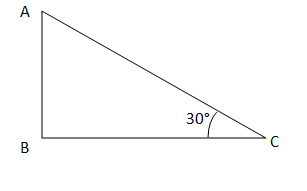

设5岁以下儿童的滑梯由ABC表示，大龄儿童的滑梯由PQR表示。

AB = 1.5米，PQ = 3米。

在ABC中，我们有

sin C = AB/AC

sin 30° = 1.5/AC

1/2 = 1.5/AC

AC = 3米

在PQR中，我们有

sin R = PQ/PR

sin 60° = 3/PR

√3/2 = 3/PR

PR = 6/√3米

有理化，

6/√3 × √3/√3 = 2√3米

因此，年幼儿童的滑梯长度为3米，

大龄儿童的滑梯长度为2√3米。

4. 从离塔基30米处的地面上的一个点看，塔顶的仰角为30°。求塔的高度。

解决方案

设AB为塔，C为离塔基B处30米的点。

tan C = AB/BC

tan 30° = AB/30

1/√3 = AB/30

AB = 30/√3米

有理化，

30/√3 × √3/√3 = 10√3米

因此，塔的高度为10√3米。

5. 一只风筝在离地面60米的高度飞行。与风筝相连的绳子暂时系在地面上的一个点。绳子与地面的倾角为60°。求绳子的长度，假设绳子没有松弛。

解决方案

设PQ为风筝离地面的高度，PR为与风筝相连的绳子。

sin R = PQ/PR

sin 60° = 60/PR

√3/2 = 60/PR

PR = 120/√3米

有理化，

120/√3 × √3/√3 = 40√3米

因此，假设绳子没有松弛，绳子的长度为40√3米。

6. 一个1.5米高的男孩站在离30米高的建筑物一定距离处。当他走向建筑物时，从他的眼睛仰望建筑物顶端的仰角从30°增加到60°。求他朝建筑物走去的距离。

解决方案

设上图表示给定的情况。

AE = 建筑物高度 = 30米

CF = 男孩身高 = 1.5米

BC = 男孩与建筑物之间的距离

DC = 男孩从原始位置C移动的距离

在ABC中，我们有

tan C = AB/BC

tan 30° = (AE - CF)/BC

1/√3 = (30 - 1.5)/BC

BC = 28.5√3米

在ABD中，我们有

tan D = AB/BD

tan 60° = 28.5/BD

√3 = 28.5/BD

BD = 28.5/√3米

有理化，

28.5/√3 × √3/√3 = 9.5√3米

CD = BC - BD = 28.5√3米 - 9.5√3米

= 19√3米

因此，男孩朝建筑物走去了19√3米。

7. 从地面上的一个点看，固定在20米高建筑物顶部的一个传输塔的底部和顶部的仰角分别为45°和60°。求塔的高度。

解决方案

设AB为建筑物顶部的传输塔，BC为建筑物。E为地面上的点。

在BCE中，我们有

tan CEB = BC/CE

tan 45° = 20/CE

1 = 20/CE

CE = 20米

在ACE中，我们有

tan CEA = AC/CE

tan 60° = AC/20

√3 = AC/20

AC = 20√3米

传输塔的高度 = AB = AC - BC = 20√3 - 20 = 20(√3 - 1)米

因此，传输塔的高度为20(√3 - 1)米。

8. 一个1.6米高的雕像矗立在一个基座的顶部。从地面上的一个点看，雕像顶部的仰角为60°，从同一点看基座顶部的仰角为45°。求基座的高度。

解决方案

设AB为基座BC上的雕像，E为地面上的点。

在ACE中，我们有

tan CEA = AC/CE

tan 60° = (AB + BC)/CE

√3 = (1.6 + BC)/CE

(1.6 + BC)/√3 = CE

在BCE中，我们有

tan CEB = BC/CE

tan 45° = BC/CE

1 = BC/CE

CE = BC

因此，

(1.6 + BC)/√3 = BC

1.6 + BC = BC√3

1.6 = BC(√3 - 1)

BC = 1.6/(√3 - 1)

有理化，

BC = 1.6/(√3 - 1) × (√3 + 1)/(√3 + 1)

BC = 1.6(√3 + 1)/2

BC = 0.8(√3 + 1)米

因此，基座的高度为0.8(√3 + 1)米。

9. 从塔脚看楼顶的仰角为30°，从楼脚看塔顶的仰角为60°。如果塔高50米，求楼的高度。

解决方案

设AB为楼，DC为塔。

在BCD中，我们有

tan B = DC/BC

tan 60° = 50/BC

√3 = 50/BC

BC = 50/√3

有理化，

BC = 50/√3 × √3/√3

= 50√3/3米

在ABC中，我们有

tan C = AB/BC

1/√3 = AB/(50√3/3)

AB = 50/3米

因此，楼的高度为50/3米。

10. 两根等高的灯杆分别立在马路的两侧，马路宽80米。从路上的一个点看，灯杆顶端的仰角分别为60°和30°。求灯杆的高度以及该点到灯杆的距离。

解决方案

设AB和DC为路BC上的灯杆，E为路上的点。

在DCE中，我们有

tan E = CD/EC

tan 30° = CD/EC

1/√3 = CD/EC

CD = EC/√3

在ABE中，我们有

tan E = AB/BE

tan 60° = AB/BE

√3 = AB/BE

AB = BE√3

我们知道AB = CD（已知）。因此，

EC/√3 = BE√3

我们也知道EC = 80 - BE。因此，

(80 - BE)/√3 = BE√3

80 - BE = 3BE

80 = 4BE

BE = 20米

因此，

EC = 80 - 20 = 60米

AB = CD = 20√3米

因此，灯杆的高度为20√3米，该点到灯杆的距离分别为20米和60米。

11. 一座电视塔垂直矗立在运河的一岸。从运河另一岸正对塔的点看，塔顶的仰角为60°。从离这一点20米远的、沿着连接该点和塔脚的直线上的另一点看，塔顶的仰角为30°（见图9.12）。求塔的高度和运河的宽度。

解决方案

在ABD中，我们有

tan D = AB/BD

tan 30° = AB/BD

1/√3 = AB/(20 + BC)

AB = (20+BC)/√3

在ABC中，我们有

tan C = AB/BC

tan 60° = AB/BC

√3 = AB/BC

AB = √3 BC

因此，

√3 BC = (20 + BC)/√3

3BC = 20 + BC

2 BC = 20

BC = 10米

AB = 10√3米

因此，塔的高度为10√3米，运河的宽度为10米。

12. 从7米高的建筑物顶部看，电缆塔顶的仰角为60°，其底部俯角为45°。确定塔的高度。

解决方案

设AB为7米高的建筑物，EC为电缆塔。AD是一条平行于地面BC的虚线。

AB = CD = 7米

在ACD中，我们有

tan A = CD/AD

tan 45° = 7/AD

1 = 7/AD

AD = 7米

在ADE中，我们有

tan A = DE/AD

tan 60° = DE/7

√3 = DE/7

DE = 7√3米

EC = DE + CD = 7√3 + 7 = 7(√3 + 1)米

因此，电缆塔的高度为7(√3 + 1)米。

13. 从海平面75米高的灯塔顶部观察，两艘船的俯角分别为30°和45°。如果一艘船正好在另一艘船的后面，位于灯塔的同一侧，则求两艘船之间的距离。

解决方案

设AB为灯塔，C和D分别为海中的船的位置。

画一条虚线AE，平行于海平面BD。

在ABC中，我们有

tan C = AB/BC

tan 45° = AB/BC

1= 75/BC

BC = 75米

在ABD中，我们有

tan D = AB/BD

tan 30° = AB/BD

1/√3 = 75/BD

BD = 75√3米

CD = BD - BC = 75√3 - 75 = 75(√3 - 1)米

因此，海中两艘船之间的距离为75(√3 - 1)米。

14. 一个1.2米高的女孩发现一个气球在风的作用下以水平直线运动，离地面高度为88.2米。在任何一个瞬间，从女孩眼睛看气球的仰角为60°。过了一段时间，仰角减小到30°（见图9.13）。求气球在此期间飞行的距离。

解决方案

设A和B为气球的初始和最终位置。设C为女孩的头部。AD和BE是从气球位置垂直于地面的虚线。

AD = BE = 88.2 - 1.2 = 87米（气球的高度不变）

在ACD中，我们有

tan C = AD/CD

tan 60° = AD/CD

√3 = 87/CD

CD = 87/√3

有理化，

CD = 87/√3 × √3/√3 = 29√3米

在BCE中，我们有

tan C = BE/CE

tan 30°= 87/CE

1/√3 = 87/CE

CE = 87√3米

DE = CE - CD = 87√3 - 29√3 = 58√3米

因此，气球飞行的距离为58√3米。

15. 一条笔直的公路通向塔的底部。塔顶的一个男人观察到一辆以匀速驶向塔底的汽车，俯角为30°。六秒后，汽车的俯角为60°。求汽车从该点到达塔底所需的时间。

解决方案

设AB为塔。设D和C为汽车的初始和最终位置。

画一条虚线AE，平行于地面。

在ABC中，我们有

tan C = AB/BC

tan 60° = AB/BC

√3 = AB/BC

BC = AB/√3

AB = √3 BC

在ABD中，我们有

tan D = AB/AD

tan 30° = AB/BD

1/√3 = AB/BD

AB = BD/√3

有理化，

AB = BD/√3 × √3/√3 = BD√3/3

因此，

BD√3/3 = √3 BC

BD = 3BC

3BC = BC + CD

2BC = CD

BC = CD/2

行驶距离CD所需时间 = 6秒

因此，行驶距离BC所需时间 = CD/2 = 6/2 = 3秒。

16. 从离塔基4米和9米处、位于同一条直线上的两个点看塔顶的仰角互为余角。证明塔的高度为6米。

解决方案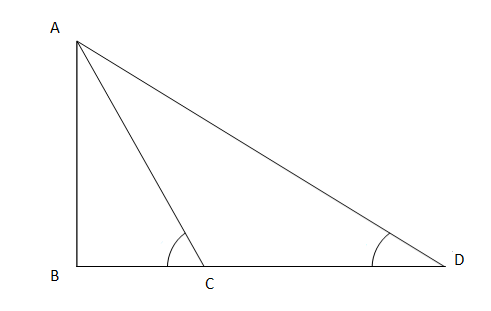

设AB为塔，C和D为地面上的两个点。

设角ACB为x，则角ABD = 90 - x

在ABC中，我们有

tan x = AB/BC

tan x = AB/4

AB = 4 tan x

在ABD中，我们有

tan (90°-x) = AB/BD

cot x = AB/9

AB = 9 cot x

将得到的两个方程相乘

AB² = 36 tan x cot x

AB² = 36 tan x (1/tan x)

AB² = 36

AB = 6米（高度不能为负）。

因此，已证明塔的高度为6米。