NCERT六年级数学第七章分数解决方案17 Mar 2025 | 阅读38分钟 练习 7.11. 写出表示阴影部分的でしょうか。 i.  答案 2/4 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 2 总部分的数量 = 4 分数 = 2/4 ii.  答案 8/9 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 8 总部分的数量 = 9 分数 = 8/9 iii.  答案 4/8 解释: 分数 = 阴影球的数量/总球的数量 阴影球的数量 = 4 总球的数量 = 8 分数 = 4/8 iv.  答案 1/4 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 1 总部分的数量 = 4 分数 = � v.  答案 3/7 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 3 总部分的数量 = 7 分数 = 3/7 vi.  答案 3/12 解释: 分数 = 阴影花的数量/总花的数量 阴影花的数量 = 3 总花的数量 = 12 分数 = 3/12 vii.  答案 10/10 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 10 总部分的数量 = 10 分数 = 10 这意味着所有部分都被涂上了颜色。 viii.  答案 4/9 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 4 总部分的数量 = 9 分数 = 4/9 ix.  答案 4/8 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 4 总部分的数量 = 8 分数 = 4/8 x. 答案 1/2 解释: 分数 = 阴影部分的数量/总部分的数量 阴影部分的数量 = 1 总部分的数量 = 2 分数 = 1/2 2. 根据给出的分数给部分涂上颜色。 i. 1/6 这意味着在总共6个部分中,有1个部分被涂上了颜色。所以,这里我们只涂上给定图形的一个部分。  ii. 1/4 这意味着在总共4个部分中,有1个部分被涂上了颜色。所以,这里我们只涂上给定图形的一个部分。  iii. 1/3 这意味着在总共3个部分中,有1个部分被涂上了颜色。所以,这里我们只涂上给定图形的一个部分。  iv. 3/4 这意味着在总共4个部分中,有3个部分被涂上了颜色。所以,这里我们只涂上给定图形的三个部分。  v. 4/9 这意味着在总共9个部分中,有4个部分被涂上了颜色。所以,这里我们只涂上给定图形的四个部分。  3. 找出错误,如果有的话。  上面显示的所有图形都是不正确的。 解释: 分数代表阴影部分除以总部分。表示分数的每个部分都是等大的。上面三个图形中的部分尺寸不同,这是不正确的。因此,我们可以说给定图形中的阴影部分不代表一个分数。 4. 一天是8小时,占全天的几分之几? 答案 8/24 一天总共有24小时 所以,一天8小时的分数是8/24 5. 一小时是40分钟,占一小时的几分之几? 答案 40/60 一小时总共有60分钟 所以,一小时40分钟的分数是40/60 6. Arya、Abhimanyu 和 Vivek 一起吃午饭。Arya 带了两个三明治,一个是蔬菜的,一个是果酱的。另外两个男孩忘了带午饭。Arya 同意分享他的三明治,以便每个人都能平等地分享每个三明治。 (a) Arya 如何分配他的三明治,才能让每个人都得到公平的份额? 答案: 男孩总数 = 3 Arya 需要将每个三明治分成三等份,这样每个男孩都能公平地分享蔬菜三明治和果酱三明治。 分数 = 一个三明治/男孩总数 = 1/3 (b) 每个男孩会得到三明治的几分之几? 答案: 三明治总数 = 2 男孩总数 = 3 每个人得到的份额 = 2/3 因此,每个男孩将得到2/3块三明治。 7. Kanchan 给连衣裙染色。她需要染30件连衣裙。她至今已经完成了20件。她完成了连衣裙的几分之几? 答案 2/3 解释: 连衣裙总数 = 30 Kanchan 完成的连衣裙数量 = 20 她完成的连衣裙的分数 = 完成的连衣裙数量/连衣裙总数 分数 = 20/30 将分子和分母都除以10,我们得到 她完成的连衣裙的分数 = 2/3 8. 写出从2到12的自然数。其中有几分之几是素数? 答案 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; 5/11 解释: 从2到12的自然数是 2、3、4、5、6、7、8、9、10、11 和 12。 从2到12的自然数总数 = 11 2到12之间的素数是 2、3、5、7 和 11 从2到12的素数总数 = 5 因此,素数的比例 = 从2到12的素数总数/从2到12的自然数总数 = 5/11 9. 写出从102到113的自然数。其中有几分之几是素数? 答案 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113; 4/12 解释: 从102到113的自然数是 102、103、104、105、106、107、108、109、110、111、112 和 113。 从102到113的自然数总数 = 12 102到113之间的素数是 103、107、109 和 113 从102到113的素数总数 = 4 因此,素数的比例 = 从102到113的素数总数/从102到113的自然数总数 = 4/12 10. 这些圆中有几分之几带有X?  答案 4/8 解释: 圆的总数 = 8 带有X的圆的数量 = 4 带有X的圆的比例 = 带有X的圆的数量/圆的总数 带有X的圆的比例 = 4/8 将分子和分母都除以4,我们得到 带有X的圆的比例 = ½ 因此,4/8和1/2都是这个问题的答案。 11. Kristin 在生日时收到一个 CD 播放器。她买了3张 CD,收到了5张作为礼物。她买的 CD 占总数的几分之几,收到的 CD 占总数的几分之几? 答案 3/8, 5/8 解释: Kristin 生日购买的 CD 数量 = 3 生日收到的 CD 数量 = 5 CD 总数 = 5 + 3 = 8 购买的 CD 的比例 = 购买的 CD 数量/CD 总数 购买的 CD 的比例 = 3/8 收到的 CD 的比例 = 收到的 CD 数量/CD 总数 收到的 CD 的比例 = 5/8 练习 7.21. 画出数轴并定位点 (a) 1/2, 1/4, 3/4, 4/4  (b) 1/8, 2/8, 3/8, 7/8  (c) 2/5, 3/5, 8/5, 4/5 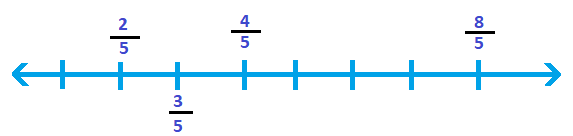 2. 将下列分数表示为带分数 (a) 20 /3 答案 6 2/3 说明 当20除以3时 6 × 3 = 18 余数 = 20 - 18 = 2 商 = 6 带分数 = 商 余数/除数 带分数 = 6 2/3 (b) 11/ 5 答案 2 1/5 说明 当11除以5时 5 × 2 = 10 余数 = 11 - 10 = 1 商 = 2 带分数 = 商 余数/除数 带分数 = 2 1/5 (c) 17 /7 答案 2 3/7 说明 当17除以7时 7 × 2 = 14 余数 = 17 - 14 = 3 商 = 2 带分数 = 商 余数/除数 带分数 = 2 3/7 (d) 28/ 5 答案 5 3/5 说明 当28除以5时 5 × 5 = 25 余数 = 28 - 25 = 3 商 = 5 带分数 = 商 余数/除数 带分数 = 5 3/5 (e) 19 /6 答案 3 1/6 说明 当19除以6时 6 × 3 = 18 余数 = 19 - 18 = 1 商 = 3 带分数 = 商 余数/除数 带分数 = 3 1/6 (f) 35/ 9 答案 3 8/9 说明 当35除以9时 9 × 3 = 27 余数 = 35 - 27 = 8 商 = 3 带分数 = 商 余数/除数 带分数 = 3 8/9 3. 将下列分数表示为假分数 (a) 7 3/4 答案 31/4 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 7 ¾ = (7 × 4 + 3)/4 = 31/4 (b) 5 6/7 答案 41/7 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 5 6/7= (5 × 7 + 6)/7 = 41/7 (c) 2 5/6 答案 17/6 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 2 5/6 = (2 × 6 + 5)/6 = 17/6 (d) 10 3/5 答案 53/5 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 10 3/5 = (10 × 5 + 3)/5 = 53/5 (e) 9 3/7 答案 66/7 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 9 3/7= (9 × 7 + 3)/7 = 66/7 (f) 8 4/9 答案 76/9 说明 假分数 = 被除数/除数 带分数 = 商 余数/除数 将带分数转换为假分数, 假分数 = (商 × 除数 + 余数) / 除数 8 4/9 = (8 × 9 + 4)/9 = 76/9 练习 7.3写出分数。这些分数都相等吗? a. 答案  分数 = 阴影部分/给定图形的总部分数 分数 = 1/2  分数 = 阴影部分/给定图形的总部分数 分数 = 2/4 将分子和分母都除以2,我们得到 分数 = 1/2  分数 = 阴影部分/给定图形的总部分数 分数 = 3/6 将分子和分母都除以3,我们得到 分数 = 1/2  分数 = 阴影部分/给定图形的总部分数 分数 = 4/8 将分子和分母都除以4,我们得到 分数 = 1/2 因此,我们可以说所有这些分数都是相等的。 b. 答案  分数 = 阴影圆/给定图形的总圆数 分数 = 4/12 将分子和分母都除以4,我们得到 分数 = 1/3  分数 = 阴影圆/给定图形的总圆数 分数 = 3/9 将分子和分母都除以3,我们得到 分数 = 1/3  分数 = 阴影圆/给定图形的总圆数 分数 = 2/6 将分子和分母都除以2,我们得到 分数 = 1/3  分数 = 阴影圆/给定图形的总圆数 分数 = 1/3  分数 = 阴影圆/给定图形的总圆数 分数 = 6/15 将分子和分母都除以3,我们得到 分数 = 2/5 因此,所有这些分数都不相等,因为最后一个分数等于2/5,而其他分数等于1/3。 2. 写出分数,并将每行的等值分数配对。 (a)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 1 总部分的数量 = 2 分数 = 1/2 (b)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 4 总部分数 = 6 分数 = 4/6 将分子和分母都除以2,我们得到 分数 = 2/3 这是最简分数形式,即分子和分母只有1作为公因数。 (c)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 3 总部分的数量 = 9 分数 = 3/9 将分子和分母都除以3,我们得到 分数 = 1/3 (d)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 2 总部分的数量 = 8 分数 = 2/8 将分子和分母都除以2,我们得到 分数 = 1/4 (e)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 3 总部分的数量 = 4 分数 = 3/4 上述分数已处于最简形式。 (i)  分数 = 阴影三角形/给定图形的总三角形数 阴影三角形 = 6 总三角形数 = 18 分数 = 6/18 将分子和分母都除以6,我们得到 分数 = 1/3 (ii)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 4 总部分的数量 = 8 分数 = 4/8 将分子和分母都除以4,我们得到 分数 = 1/2 (iii)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 12 总部分数 = 16 分数 = 12/16 将分子和分母都除以4,我们得到 分数 = 3/4 (iv)  分数 = 阴影部分/给定图形的总部分数 阴影部分 = 8 总部分数 = 12 分数 = 8/12 将分子和分母都除以4,我们得到 分数 = 2/3 (v)  分数 = 阴影三角形/给定图形的总三角形数 阴影三角形 = 4 总三角形数 = 16 分数 = 4/16 将分子和分母都除以4,我们得到 分数 = 1/4 为了配对等值分数,让我们将所有上面的答案表示在一个表格中。
因此,等值分数是 (a)- (ii) 3. 在下列各数中用正确的数字替换 A 这里我们将块视为A。 (a)  答案 28 说明 2 × A = 8 × 7 展开数字8 2 × A = 2 × 4 × 7 比较两边,我们得到 A = 4 × 7 A = 28 (b)  答案 16 说明 5 × A = 8 × 10 展开数字10 5 × A = 8 × 2 × 5 5 × A =5 × 8 × 2 比较两边,我们得到 A = 8 × 2 A = 16 (c)  答案 12 说明 3 × 20 = A × 5 展开数字20 3 × 4 × 5 = A × 5 比较两边,我们得到 A = 3 × 4 A = 12 (d)  答案 20 说明 45 × A = 60 × 15 展开数字60 45 × A = 3 × 20 × 15 45 × A = 3 × 15 × 20 45 × A = 45 × 20 比较两边,我们得到 A = 20 (e)  答案 3 说明 18 × 4 = 24 × A 展开数字18 6 × 3 × 4 = 24 × A 6 × 4 × 3 = 24 × A 24 × 3 = 24 × A 比较两边,我们得到 A = 3 4. 找到分子为3/5的等值分数,其 (a) 分母为20 答案 12/20 说明 设分子为A。 3/5 = A/20 3 × 20 = 5 × A 展开数字20 3 × 5 × 4 = 5 × A 5 × 4 × 3 = 5 × A 5 × 12 = 5 × A 比较两边,我们得到 A = 12 分数 = 12/20 因此,分数3/5的等值是12/20,其中12是分子,20是分母。 (b) 分子为9 答案 9/15 说明 设分母为A。 3/5 = 9/A 3 × A = 5 × 9 展开数字9 3 × A = 5 × 9 3 × A = 5 × 3 × 3 3 × A = 3 × 3 × 5 比较两边,我们得到 A = 3 × 5 A = 15 分数 = 9/15 因此,分数3/5的等值是9/15,其中9是分子,15是分母。 (c) 分母为30 答案 18/30 说明 设分子为A。 3/5 = A/30 3 × 30 = 5 × A 展开数字30 3 × 5 × 6 = 5 × A 5 × 6 × 3 = 5 × A 5 × 18 = 5 × A 比较两边,我们得到 A = 18 分数 = 18/30 因此,分数3/5的等值是18/30,其中18是分子,30是分母。 (d) 分子为27 答案 27/45 说明 设分母为A。 3/5 = 27/A 3 × A = 5 × 27 展开数字27 3 × A = 5 × 9 3 × A = 5 × 9 × 3 3 × A = 3 × 9 × 5 比较两边,我们得到 A = 9 × 5 A = 45 分数 = 27/45 因此,分数3/5的等值是27/45,其中27是分子,45是分母。 5. 找到36/48的等值分数,其 (a) 分子为9 答案 9/12 说明 设分母为A。 36/48 = 9/A 36 × A = 9 × 48 展开数字48 36 × A = 9 × 12 × 4 36 × A = 9 × 4 × 12 36 × A = 36 × 12 比较两边,我们得到 A = 12 分数 = 9/12 因此,分数36/48的等值是9/12,其中9是分子,12是分母。 (b) 分母为4 答案 3/4 说明 设分子为A。 36/48 = A/4 36 × 4 =48 × A 展开数字36 3 × 12 × 4 = 48 × A 12 × 4 × 3 = 48 × A 48 × 3 = 48 × A 比较两边,我们得到 A = 3 分数 = 3/4 因此,分数36/48的等值是3/4,其中3是分子,4是分母。 6. 检查给定的分数是否相等 要检查等值分数,我们将把分数转换为最简形式,即分数中分子和分母都只有一个公因数1。 (a) 5/9, 30/54 答案: 是的,给定的分数是相等的 说明 第一种分数 5/9已处于最简形式。 第二种分数 让我们考虑第二种分数。 30的因数:2 × 5 × 3 54的因数:2 × 3 × 3 × 3 公因数 = 2 × 3 = 6 将30/54的分子和分母都除以6,我们得到 5/9 因此,两个分数是相等的。 (b) 3/10, 12/50 答案: 否,给定的分数不相等。 说明 第一种分数 3/10已处于最简形式。 第二种分数 让我们考虑第二种分数。 12的因数:2 × 2 × 3 50的因数:2 × 5 × 5 公因数 = 2 将12/50的分子和分母都除以2,我们得到 6/25 因此,两个分数不相等。 3/10不等于6/25 (c) 7/13, 5/11 答案: 否,给定的分数不相等 说明 第一种分数 7/13已处于最简形式。 第二种分数 5/11也已处于最简形式。 因此,两个分数不相等。 7. 将下列分数化为最简形式 (a) 48/60 答案 4/5 说明 48的因数:2 × 2 × 2 × 2 × 3 60的因数:2 × 2 × 3 × 5 公因数:2 × 2 × 3 = 12 将给定分数的分子和分母都除以12,我们得到 4/5 因此,4/5是48/60的最简形式。 (b) 150/ 60 答案 5/2 说明 150的因数:3 × 5 × 2 × 5 60的因数:2 × 2 × 3 × 5 公因数:2 × 3 × 5 = 30 将给定分数的分子和分母都除以30,我们得到 5/2 因此,5/2是150/60的最简形式。 (c) 84/98 答案 6/7 说明 84的因数:2 × 2 × 7 × 3 98的因数:2 × 7 × 7 公因数:2 × 7 = 14 将给定分数的分子和分母都除以14,我们得到 6/7 因此,6/7是84/98的最简形式。 (d) 12/52 答案 3/13 说明 12的因数:2 × 2 × 3 52的因数:2 × 2 × 13 公因数:2 × 2 = 4 将给定分数的分子和分母都除以4,我们得到 3/13 因此,3/13是12/52的最简形式。 (e) 7/28 答案 1/4 说明 7的因数:1 × 7 28的因数:2 × 2 × 7 公因数:7 将给定分数的分子和分母都除以7,我们得到 1/4 因此,1/4是7/28的最简形式。 8. Ramesh 有20支铅笔,Sheelu 有50支铅笔,Jamaal 有80支铅笔。4个月后,Ramesh 用掉了10支铅笔,Sheelu 用掉了25支铅笔,Jamaal 用掉了40支铅笔。每个人用掉了几分之几的铅笔?检查他们是否用掉了相同比例的铅笔? 答案: 1/2, 1/2, 1/2;是 说明 Ramesh 的铅笔总数 = 20 Ramesh 用掉的铅笔数量 = 10 分数 = 用掉的铅笔/总铅笔数 分数 = 10/20 = 1/2 因此,Ramesh 用掉了1/2比例的铅笔。 Sheelu 的铅笔总数 = 50 Sheelu 用掉的铅笔数量 = 25 分数 = 用掉的铅笔/总铅笔数 分数 = 25/50 = 1/2 因此,Sheelu 用掉了1/2比例的铅笔。 Jamaal 的铅笔总数 = 80 Jamaal 用掉的铅笔数量 = 40 分数 = 用掉的铅笔/总铅笔数 分数 = 40/80 = 1/2 因此,Jamaal 也用掉了1/2比例的铅笔。 是的,他们每个人都用掉了相同比例的铅笔。 9. 将等值分数配对,并为每个分数写出另外两个。 在这里,我们将给定的分数转换为最简分数,以便与给定的值进行匹配。
练习 7.41. 写出阴影部分作为分数。使用分数之间的正确符号将它们按升序和降序排列 (a) 答案 升序:1/8 < 3/8 < 4/8 < 6/8 降序:6/8 > 4/8 > 3/8 > 1/8 说明  阴影部分的数量 = 3 总部分的数量 = 8 分数 = 阴影部分/总部分数 分数 = 3/8  阴影部分的数量 = 6 总部分的数量 = 8 分数 = 阴影部分/总部分数 分数 = 6/8  阴影部分的数量 = 4 总部分的数量 = 8 分数 = 阴影部分/总部分数 分数 = 4/8  阴影部分的数量 = 1 总部分的数量 = 8 分数 = 阴影部分/总部分数 分数 = 1/8 要比较分数,我们需要确保分数有相同的分母。 数字的升序是从最小分数到最大分数的顺序。 1/8 < 3/8 < 4/8 < 6/8 数字的降序是从最大分数到最小分数的顺序。 6/8 > 4/8 > 3/8 > 1/8 (b) 答案 升序:3/9 < 4/9 < 6/9 < 8/9 降序:8/9 > 6/9 > 4/9 > 3/9 说明  阴影部分的数量 = 8 总部分的数量 = 9 分数 = 阴影部分/总部分数 分数 = 8/9  阴影部分的数量 = 4 总部分的数量 = 9 分数 = 阴影部分/总部分数 分数 = 4/9  阴影部分的数量 = 3 总部分的数量 = 9 分数 = 阴影部分/总部分数 分数 = 3/9  阴影部分的数量 = 6 总部分的数量 = 9 分数 = 阴影部分/总部分数 分数 = 6/9 要比较分数,我们需要确保分数有相同的分母。 数字的升序是从最小分数到最大分数的顺序。 3/9 > 4/9 > 6/9 > 8/9 数字的降序是从最大分数到最小分数的顺序。 8/9 > 6/9 >4/9 > 3/9 (c) 在数轴上显示 2/6, 4/6, 8/6, 和 6/6。 数轴  在给出的分数之间填入合适的符号。 5/6 > 2/6 由于两个分母相同,分数5/6大于分数2/6。 3/6 > 0 3/6 > 0/6 我们也可以将0写成0/6。任何数除以任何数都等于0。 由于两个分母现在相同,分数3/6大于分数0/6或0。 1/6 < 6/6 分数6/6大于分数1/6。 8/6 > 5/6 分数8/6大于分数5/6。 2. 比较分数并填入合适的符号。 (a) 3/6 < 5/6 解释: 分数5/6大于分数3/6,因为数字5大于数字3。 (b) 1/7 < 1/4 说明 这里,分母不同。要比较分数,我们需要相同的分母。 所以,将左边的分数乘以4。 1 × 4/ (7 × 4) = 4/28 同样,将右边的分数乘以7。 1 × 7/ (4 × 7) = 7/28 现在,比较两个分数, 4/28 < 7/28 故, 1/7 < 1/4 (c) 4/5 < 5/5 解释: 分数4/5小于分数5/5。 (d) 3/5 > 3/7 说明 这里,分母不同。要比较分数,我们需要相同的分母。 所以,将左边的分数乘以7。我们可以选择任何倍数使分母相等。 3 × 7/ (5 × 7) = 21/35 同样,将右边的分数乘以5 3 × 5/ (7 × 5) = 15/35 现在,比较两个分数, 21/35 > 15/35 故, 3/5 > 3/7 3. 再造五个类似的对子,并填入合适的符号。 答案: 再造五个类似的对子如下:
4. 看图,并在给定的分数对之间填入“<”、“>”或“=”号。  上面的所有数字都按升序排列。 (a) 1/6 < 1/3 为了比较,给定分数的denominator必须相等。 将右边的分数乘以2,我们得到 1 × 2/ (3 × 2) = 2/6 现在比较, 1/6 < 2/6 故, 1/6 < 1/3 (b) 3/4 > 2/6 为了比较,给定分数的denominator必须相等。 将左边的分数乘以3,我们得到 3 × 3/ (4 × 3) = 9/12 将右边的分数乘以2,我们得到 2 × 2/ (6 × 2) = 4/12 现在比较, 9/12 > 4/12 故, 3/4 > 2/6 (c) 2/3 > 2/4 为了比较,给定分数的denominator必须相等。 将左边的分数乘以4,我们得到 2 × 4/ (3 × 4) = 8/12 将右边的分数乘以3,我们得到 2 × 3/ (4 × 3) = 6/12 现在比较, 8/12 > 6/12 故, 2/3 > 2/4 (d) 6/6 = 3/3 一个数除以它本身总是等于1。 1 = 1 故, 6/6 = 3/3 (e) 5/6 < 5/5 为了比较,给定分数的denominator必须相等。 将左边的分数乘以5,我们得到 5 × 5/ (6 × 5) = 25/30 将右边的分数乘以3,我们得到 2 × 3/ (4 × 3) = 6/12 现在比较, 8/12 > 6/12 故, 2/3 > 2/4 5. 你能多快完成这个?填入合适的符号。(‘<’、‘>’或‘=’)。。 a. 1/2 > 1/5 为了比较,给定分数的denominator必须相等。 将左边的分数乘以5,我们得到 1 × 5/ (2 × 5) = 5/10 将右边的分数乘以2,我们得到 1 × 2/ (5 × 2) = 2/10 现在比较, 5/10 > 2/10 故, 1/2 > 1/5 b. 2/4 = 3/6 为了比较,给定分数的denominator必须相等。两个给定的分数都不是最简形式。所以,我们先将两个分数都化为最简形式。 将左边的分数除以2,我们得到 1/2 将右边的分数除以3,我们得到 1/2 现在比较, 1/2= 1/2 故, 2/4 = 3/6 c. 3/5 < 2/3 为了比较,给定分数的denominator必须相等。 将左边的分数乘以3,我们得到 3 × 3/ (5 × 3) = 9/15 将右边的分数乘以5,我们得到 2 × 5/ (3 × 5) = 10/15 现在比较, 9/15 < 10/15 故, 1/2 > 1/5 3/5 < 2/3 d. 3/4 > 2/8 为了比较,给定分数的denominator必须相等。 第二个分数可以化为最简形式。 将右边的分数除以2,我们得到 1/4 两个分数的denominator现在相等了。 通过比较, 3/4 > 1/4 因此, 3/4 > 2/8 e. 3/5 < 6/5 分母是相同的。 因此, 6/5大于3/5。 f. 7/9 > 3/9 分母是相同的。 因此, 7/9 > 3/9 g. 1/4 = 2/8 为了比较,给定分数的denominator必须相等。 第二个分数可以化为最简形式。 将右边的分数除以2,我们得到 1/4 两个分数的denominator现在相等了。 通过比较, � = 1/4 因此, 1/4 = 2/8 h. 6/10 < 4/5 为了比较,给定分数的denominator必须相等。 第一个分数可以化为最简形式。 将左边的分数除以2,我们得到 3/5 两个分数的denominator现在相等了。 通过比较, 3/5 < 4/5 因此, 6/10 < 4/5 i. 3/4 < 7/8 为了比较,给定分数的denominator必须相等。 将左边的分数乘以2,我们得到 3 × 2/ (4 × 2) = 6/8 现在比较, 6/8 < 7/8 故, 3/4 < 7/8 j. 6/10 = 3/5 为了比较,给定分数的denominator必须相等。 第一个分数可以化为最简形式。 将左边的分数除以2,我们得到 3/5 2 × 3 = 6 2 × 5 = 10 两个分数的denominator现在相等了。 通过比较, 3/5 = 3/5 因此, 6/10 = 3/5 k. 5/7 = 15/21 为了比较,给定分数的denominator必须相等。 第二个分数可以化为最简形式。 将右边的分数除以3,我们得到 5/7 3 × 5 = 15 3 × 7 = 21 两个分数的denominator现在相等了。 通过比较, 5/7 = 5/7 因此, 5/7 = 15/21 6. 以下分数仅表示三个不同的数字。将它们分成三组等值分数,方法是将每个分数化为最简形式。 最简形式是指分数的形式,其中分子和分母只有1作为公因数。这里,我们将找到公倍数并将分子和分母除以该公倍数。 a. 2/12 答案 1/6 解释: 将分子和分母都除以2,我们得到 1/6 2 × 1 = 2 2 × 6 = 12 b. 3/15 答案 1/5 解释: 将分子和分母都除以3,我们得到 1/5 3 × 1 = 3 3 × 5 = 15 c. 8/50 答案 4/25 解释: 将分子和分母都除以2,我们得到 4/25 2 × 4 = 8 2 × 25 = 50 d. 16 /100 答案 4/25 解释: 将分子和分母都除以4,我们得到 4/25 4 × 4 = 16 4 × 25 = 100 e. 10/60 答案 1/6 解释: 将分子和分母都除以10,我们得到 1/6 10 × 1 = 10 10 × 6 = 60 f. 15/75 答案 1/5 解释: 将分子和分母都除以15,我们得到 1/5 15 × 1 = 15 15 × 5 = 75 g. 12/60 答案 1/5 解释: 将分子和分母都除以12,我们得到 1/5 12 × 1 = 12 12 × 5 = 60 h. 16/96 答案 1/6 解释: 将分子和分母都除以16,我们得到 1/6 16 × 1 = 16 16 × 6 = 96 i. 12/75 答案 4/25 解释: 将分子和分母都除以3,我们得到 4/25 3 × 4 = 12 3 × 25 = 75 j. 12/72 答案 1/6 解释: 将分子和分母都除以12,我们得到 1/6 12 × 1 = 12 12 × 6 = 72 k. 3/18 答案 1/6 解释: 将分子和分母都除以3,我们得到 1/6 3 × 1 = 3 3 × 6 = 18 l. 4/25 上述分数已处于最简形式。 三组等值分数显示在下面的表格中
7. 找到下列问题的答案。写出来并说明你是如何解决的。 (a) 5/9 是否等于 4/5? 答案: 否 解释: 为了比较,给定分数的denominator必须相等。 将左边的分数乘以5,我们得到 5 × 5/ (9 × 5) = 25/45 将右边的分数乘以9,我们得到 9 × 4/ (5 × 9) = 36/45 通过比较, 25/45 < 36/45 因此, 5/9不等于4/5。 (b) 9/16 是否等于 5/9? 答案: 否 解释: 为了比较,给定分数的denominator必须相等。 将左边的分数乘以9,我们得到 9 × 9/ (9 × 16) = 81/144 将右边的分数乘以16,我们得到 16 × 5/ (16 × 9) = 80/144 通过比较, 81/144 > 80/144 因此, 9/16不等于5/9。 (c) 4/5 是否等于 16/20? 答案: 是 解释: 让我们将第二个分数转换为最简形式。 将分子和分母都除以4,我们得到 (4 × 4)/(4 × 5) = 4/5 与第一个分数比较, 4/5 = 4/5 因此, 4/5等于16/20。 (d) 1/15 是否等于 4/30? 答案: 否 解释: 让我们将第二个分数转换为最简形式。 将分子和分母都除以2,我们得到 (2 × 2)/(2 × 15) = 2/15 与第一个分数比较, 1/15 < 2/15 因此, 1/15不等于4/30。 8. Ila 读了一本100页的书中的25页。Lalita 读了这本书的2/5。谁读得少? 答案: Ila 读得少 解释: Ila 读的页数 = 25 Lalita 读的页数 = 分数 × 书的总页数 = 2/5 × 100 = 200/5 = 40 Lalita 读的页数 = 40 因此,Lalita 读了40页,Ila 读了25页。 9. Rafiq 锻炼了1/6小时,而 Rohit 锻炼了3/4小时。谁锻炼的时间更长?长多少? 答案: Rohit 锻炼的时间更长 解释: 1小时 = 60分钟 Rafiq 锻炼的分钟数 = 分数 × 分钟数 = 3/6 × 60 = 30分钟 Rohit 锻炼的分钟数 = 分数 × 分钟数 = 3/4 × 60 = 45分钟 因此,Rohit 锻炼了45分钟,Rafiq 锻炼了30分钟。 10. A班有25名学生,20名学生得分60%或更高;B班有30名学生,24名学生得分60%或更高。哪个班级获得60%或更高分数的学生比例更大? 答案: 两个班级获得一等成绩的学生比例相同(4/5)。 解释: A班学生人数 = 25 A班得分60%或更高分数的学生人数 = 20 及格学生比例 = 及格学生人数/总学生人数 = 20/25 = 4/5 A班及格学生比例 = 4/5 B班学生人数 = 30 B班得分60%或更高分数的学生人数 = 24 及格学生比例 = 及格学生人数/总学生人数 = 24/30 = 4/5 B班及格学生比例 = 4/5 因此,两个班级及格的学生比例相等。 练习7.51. 以加法或减法形式写出这些分数  答案: + (加法) 说明 在这里,我们首先计算每个部分的比例。  分数 = 阴影部分/总部分数 阴影部分 = 1 总部分数 = 5 分数 = 1/5  分数 = 阴影部分/总部分数 阴影部分 = 2 总部分数 = 5 分数 = 2/5  分数 = 阴影部分/总部分数 阴影部分 = 3 总部分数 = 5 分数 = 3/5 这表明, 1/5 + 2/5 = 3/5 因此,它表示加法。   答案: - (减法) 说明  分数 = 阴影部分/总部分数 阴影部分 = 5 总部分数 = 5 分数 = 5/5  分数 = 阴影部分/总部分数 阴影部分 = 3 总部分数 = 5 分数 = 3/5  分数 = 阴影部分/总部分数 阴影部分 = 2 总部分数 = 5 分数 = 2/5 这表明, 5/5 - 3/5 = 2/5 因此,它表示减法。   答案: + (加法) 说明  分数 = 阴影部分/总部分数 阴影部分 = 2 总部分数 = 6 分数 = 2/6  分数 = 阴影部分/总部分数 阴影部分 = 3 总部分数 = 6 分数 = 3/6  分数 = 阴影部分/总部分数 阴影部分 = 5 总部分数 = 6 分数 = 5/6 因此, 2/6 + 3/6 = 5/6 上述分数表示加法。  2. 求解 (a) 1/18 + 1/18 答案: 2/18 或 1/9 说明 对于加法,分母必须相同。 1/18 + 1/18 = (1 + 1)/18 = 2/18 分子和分母都有2作为公因数。让我们将分数除以2,化为最简形式。 1/9 2 × 1 = 2 2 × 9 = 18 因此, 1/18 + 1/18 = 1/9 (b) 8/15 + 3/15 对于加法,分母必须相同。 答案 11/15 说明 8/15 + 3/15 = (8 + 3)/15 = 11/15 该分数已处于最简形式。 11/15 (c) 7/7 - 5/7 答案 2/7 说明 7/7 - 5/7 = (7 - 5)/7 = 2/7 该分数已处于最简形式。 2/7 (d) 1/22 + 21/22 答案 1 说明 1/22 + 21/22 = (1 + 21)/22 = 22/22 分子和分母都有22作为公因数。让我们将分数除以22,化为最简形式。 1/1 22 × 1 = 22 因此, 1/22 + 21/22 = 1 (e) 12/15 - 7/15 答案 5/15 说明 12/15 - 7/15 = (12 - 7)/15 = 5/15 分子和分母都有5作为公因数。让我们将分数除以5,化为最简形式。 1/3 5 × 1 = 5 5 × 3 = 15 因此, 12/15 - 7/15 = 1/3 (f) 5/8 + 3/8 答案 1 说明 5/8 + 3/8 = (5 + 3)/8 = 8/8 分子和分母都有8作为公因数。让我们将分数除以8,化为最简形式。 1/1 8 × 1 = 8 因此, 5/8 + 3/8 = 1 (g) 1 - 2/3 答案 1/3 说明 1/1 - 2/3 为了相减,分母必须相等。 我们可以写任何数字的分母为1。 例如: 1 可以写成 1/1 将分数(1/1)乘以3,我们得到 3/3 1 × 3/ 1 × 3 = 3/3 现在相减, 3/3 - 2/3 = (3 - 2)/3 = 1/3 (h) 1/4 + 0/4 答案 1/4 说明 1/4 + 0/4 = (1 + 0)/4 = 1/4 (i) 3 - 12/5 答案 3/5 解释: 为了相减,分母必须相等。 我们可以写任何数字的分母为1。 例如: 3 可以写成 3/1 将分数(3/1)乘以5,我们得到 5 × 3/ 1 × 5 = 15/5 现在相减, 15/5 - 12/5 = (15 - 12)/5 =3/5 3. Shubham 漆了他房间墙壁空间的2/3。他的姐姐 Madhavi 帮忙漆了墙壁空间的1/3。他们一起漆了多少? 答案: Shubham 漆的墙壁比例 = 2/3 Madhavi 漆的墙壁比例 = 1/3 一起漆的总墙壁 = 2/3 + 1/3 = (2 + 1)/3 = 3/3 将分子和分母都除以3,我们得到 1/1 因此,Shubham 和 Madhavi 一起漆了整面墙。 4. 填入缺失的分数。 (a) 7/10 - 3/10 答案 2/5 说明 7/10 - 3/10 = (7 - 3)/10 = 4/10 上述分数中的分子和分母有2作为公因数。将分数除以2,我们得到 2/5 2 × 2 = 4 2 × 5 = 10 (b) 8/21 ? 3/21 = 5/21 答案 8/21 说明 设空白处为A。 A - 3/21 = 5/21 A = 5/21 + 3/21 A = (5 + 3)/21 A = 8/21 = (7 - 3)/10 = 4/10 上述分数中的分子和分母有2作为公因数。将分数除以2,我们得到 2/5 2 × 2 = 4 2 × 5 = 10 (c) 6/6 - 3/6 = 3/6 答案 6/6 说明 设空白处为A。 A - 3/6 = 3/6 A = 3/6 + 3/6 A = (3 + 3)/6 A = 6/6 (d) 7/27 + 5/27 = 12/27 答案 7/27 说明 设空白处为A。 A + 5/27 = 12/17 A = 12/27 - 5/27 A = (12 - 5)/27 A = 7/27 5. Javed 得到了一篮子橙子中的5/7。篮子里还剩下多少比例的橙子? 答案:2/7 Javed 拥有的橙子比例 = 5/7 篮子里的橙子总数 = 1/1 完整的比例总是表示为1或1/1。 篮子里剩下的橙子比例 = 1/1 - 5/7 为了相减,分母必须相等。 将分数乘以7,我们得到 (1× 7)/ (1 × 7) = 7/7 现在相减, 7/7 - 5/7 = (7 - 5)/7 = 2/7 因此,篮子里剩下2/7比例的橙子。 练习7.61. 求解 (a) 2/3 + 1/7 答案 17/21 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 7 × 3 = 21 将分数(2/3)乘以7,我们得到 (2 × 7)/ (3 × 7) = 14/21 将分数(1/7)乘以3,我们得到 (1 × 3)/ (7 × 3) = 3/21 现在,相加 = 14/21 + 3/21 = 17/21 我们也可以将分数化为最简形式。但是,上面的分数已经是最简形式了,因为分子和分母只有1作为公因数。 (b)3/10 + 7/15 答案 23/30 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 将分数(3/10)乘以3,我们得到 (3 × 3)/ (10 × 3) = 9/30 将分数(7/15)乘以2,我们得到 (7 × 2)/ (15 × 2) = 14/30 现在,相加 = 9/30 + 14/30 = 23/30 (c) 4/9 + 2/7 答案 46/63 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 9 × 7 = 63 将分数(4/9)乘以7,我们得到 (4 × 7)/(9 × 7) = 28/63 将分数(2/7)乘以9,我们得到 (9 × 2)/ (7 × 9) = 18/63 现在,相加 = 28/63 + 18/63 = (28 + 18)/63 = 46/63 (d) 5/7 + 1/3 答案 22/21 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 7 × 3 = 21 将分数(5/7)乘以3,我们得到 (5 × 3)/ (3 × 7) = 15/21 将分数(1/3)乘以7,我们得到 (1 × 7)/ (7 × 3) = 7/21 现在,相加 = 15/21 + 7/21 = (15 + 7)/21 = 22/21 (e) 2/5 + 1/6 答案 17/30 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 5 × 6 = 30 将分数(2/5)乘以6,我们得到 (2 × 6)/ (5 × 6) = 12/30 将分数(1/6)乘以5,我们得到 (1 × 5)/ (6 × 5) = 5/30 现在,相加 = 12/30 + 5/30 = (12 + 5)/30 = 17/30 (f) 4/5 + 2/3 答案 22/15 解释: 为了相加,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 5 × 3 = 15 将分数(4/5)乘以3,我们得到 (4 × 3)/ (3 × 5) = 12/15 将分数(2/3)乘以5,我们得到 (2 × 5)/ (5 × 3) = 10/15 现在,相加 = 12/15 + 10/15 = (12 + 10)/15 = 22/15 (g) 3/4 - 1/3 答案 5/12 解释: 为了相减,分母必须相等。 所以,我们将两个分数都乘以一个数,使分母相等。 4 × 3 = 12 将分数(3/4)乘以3,我们得到 (3 × 3)/ (4 × 3) = 9/12 将分数(1/3)乘以4,我们得到 (1 × 4)/ (4 × 3) = 4/12 现在,相减 = 9/12 - 4/12 = (9 - 4)/12 = 5/12 (h) 5/6 - 1/3 答案: 3/6 或 1/2 解释: 为了相减,分母必须相等。。 2 × 3 = 6 这里,我们将分数(1/3)乘以2,使两个分母相等。 将分数(1/3)乘以2,我们得到 (1 × 2)/ (3 × 2) = 2/6 现在,相减, = 5/6 - 2/6 = (5 - 2)/6 = 3/6 让我们将上述分数除以2,化为最简形式。 1/2 3 × 1 = 3 3 × 2 = 6 (i) 2/3 + 3/4 + 1/2 答案 23/12 解释: 为了相加,分母必须相等。 为了使分母相等,我们将找到所有分母的LCM。 LCM (3, 4, 2) = 12 所以,我们将三个分数都乘以一个数,使分母等于12。 将分数(2/3)乘以4,我们得到 (2 × 4)/ (3 × 4) = 8/12 将分数(3/4)乘以3,我们得到 (3 × 3)/ (4 × 3) = 9/12 将分数(1/2)乘以6,我们得到 (1 × 6)/ (2 × 6) = 6/12 现在,相加 8/12 + 9/12 + 6/12 = (8 + 9 + 6)/12 = 23/12 (j)1/2 + 1/3 + 1/6 答案: 6/6 或 1 解释: 为了相加,分母必须相等。 为了使分母相等,我们将找到所有分母的LCM。 LCM (2, 3, 6) = 6 所以,我们将三个分数都乘以一个数,使分母等于6。 将分数(1/2)乘以3,我们得到 (1 × 3)/ (2 × 3) = 3/6 将分数(1/3)乘以2,我们得到 (1 × 2)/ (3 × 2) = 2/6 第三个分数已经有6作为分母。 现在,相加 3/6 + 2/6 + 1/6 = (3 + 2 + 1)/6 = 6/6 将上述分数除以6,我们得到 1/1 或 1 (k) 1 1/3 + 3 2/3 答案 5 解释: 分数和整数部分可以分开相加。 (1 + 3) + (1/3 + 2/3) = 4 + (3/3) = 4 + 1 = 5 (l) 4 2/3 + 3 1/4 答案 95/12 解释: 分数和整数部分可以分开相加。 整数部分 (4 + 3) = 7 分数部分 2/3 + 1/4 为了相加,分母必须等于12。 3 × 4 = 12 将分数(2/3)乘以4,我们得到 (2 × 4)/ (3 × 4) = 8/12 将分数(1/4)乘以3,我们得到 (1 × 3)/ (4 × 3) = 3/12 现在相加, 8/12 + 3/12 = (8 + 3)/12 = 11/12 让我们将分数部分和整数部分相加, 7 + 11/12 7/1 + 11/12 将分数(7/1)乘以12,我们得到 7 × 12/ 1 × 12 = 84/12 现在相加, 84/12 + 11/12 = 95/12 (m) 16/5 - 7/5 答案 9/5 说明 = 16/5 - 7/5 = (16 - 7)/5 = 9/5 (n) 4/3 - 1/2 答案 5/6 解释: 为了相减,分母必须相等。 为了使分母相等,我们将找到所有分母的LCM。 LCM (3, 2) = 6 所以,我们将两个分数都乘以一个数,使分母等于6。 将分数(4/3)乘以2,我们得到 (2 × 4)/ (3 × 2) = 8/6 将分数(1/2)乘以3,我们得到 (1 × 3)/ (2 × 3) = 3/6 现在相减, 8/6 - 3/6 = (8 - 3)/6 = 5/6 2. Sarita 买了2/5 米的丝带,Lalita 买了3/4 米的丝带。她们买的丝带总长度是多少? 答案 23/20 Sarita 买的丝带长度 = 2/5 米 Lalita 买的丝带长度 =3/4 米 总长度 = Sarita 买的长度 + Lalita 买的长度 = 2/5 + 3/4 让我们将分数(2/5)乘以4,将分数(3/4)乘以5,使分母等于20。 (2 × 4)/ (5 × 4) = 8/20 (3 × 5)/ (4 × 5) = 15/20 总长度 = 8/20 + 15/20 = 23/20 因此,Sarita 和 Lalita 一起买了23/20 米的丝带。 3. Naina 得到了一块1 1/2块的蛋糕,Najma 得到了一块1 1/3块的蛋糕。两人总共得到了多少蛋糕? 答案 Naina 得到的蛋糕块 = 1 1/2 Najma 得到的蛋糕块 = 1 1/3 蛋糕总量 = 1 1/2 + 1 1/3 让我们分别相加整数部分和分数部分,得到 (1 + 1) + (1/2 + 1/3) 将分数(1/2)乘以3,将分数(1/3)乘以2,得到 2 + ((1 × 3)/(2 × 3) + (1 × 2)/ (3 × 2)) = 2 + (3/6 + 2/6) = 2 + 5/6 = 2 5/6 因此,两人总共得到了2 5/6块蛋糕。 4. 填入方框。  答案 7/8 说明 设空白处为A。 A - 5/8 = 1/4 A = 1/4 + 5/8 将分数(1/4)乘以2,我们得到 (1 × 2)/ (4 × 2) = 2/8 现在相加, A = 2/8 + 5/8 A = 7/8  答案 7/10 说明 设空白处为A。 A - 1/5 = 1/2 负号移到另一边变成正号。 A = 1/2 + 1/5 将分数(1/2)乘以5,将分数(1/5)乘以2,使分母等于10,我们得到 A = 5/10 + 2/10 A = (5 + 2)/10 A = 7/10  答案 1/3 说明 设空白处为A。 1/2 - A = 1/6 A = 1/2 - 1/6 将分数(1/2)乘以3,我们得到 A = 3/6 - 1/6 A = (3 - 1)/6 A = 2/6 将分子和分母除以公因数(2),我们得到 A = 1/3 5. 完成加减方框。  6. 一根7/8米长的电线断成两截。一截长1/4米。另一截有多长? 答案: 5/8 米 电线的总长度 = 7/8 米 一截的长度 = 1/4 米 另一截的长度 = 总长度 - 一截的长度 = 7/8 - 1/4 将分数(1/4)乘以2,我们得到 = 7/8 - 2/8 = (7 - 2)/8 = 5/8 因此,另一截的长度是5/8米。 7. Nandini 的家离学校9/10公里。她走了一段距离,然后搭乘了1/2公里的公交车到达学校。她走了多远? 答案: 2/5公里 或 4/10公里 Nandini家到学校的总距离 = 9/10公里 搭乘公交车的距离 = 1/2公里 Nandini 走的路程 = 9/10 - 1/2 将第二个分数乘以5,我们得到 9/10 - 5/10 = (9 - 5)/10 = 4/10 将上述分数除以2, = 2/5 因此,Nandini 走了2/5公里到达学校。 8. Asha 和 Samuel 的书架大小相同,部分放满了书。Asha 的书架是5/6满,Samuel 的书架是2/5满。谁的书架更满?多多少? 答案: Asha;13/30 Asha 书架装书的比例 = 5/6 Samuel 书架装书的比例 = 2/5 为了比较,让我们使它们的分母相等。 将分数(5/6)乘以5,我们得到 (5 × 5)/ (6 × 5) = 25/30 将分数(2/5)乘以6,我们得到 (2 × 6)/ (5 × 6) = 12/30 通过比较, 25/30 > 12/30 因此,Asha 的书架比 Samuel 的书架更满。 差值 = 25/30 - 12/30 = (25 - 12)/30 = 13/30 因此,Asha 的书架比 Samuel 的书架多13/30。 9. Jaidev 走过操场用了 2 1/5 分钟。Rahul 用了 7/4 分钟做同样的事情。谁花的时间更少,少多少? 答案: Rahul;9/20分钟 Jaidev 走过操场用的时间 = 2 1/5 = 11/5 Rahul 走过操场用的时间 = 7/4 将分数(11/5)乘以4,我们得到 (11 × 4)/ (5 × 4) = 44/20 将分数(7/4)乘以5,我们得到 (7 × 5)/ (4 × 5) = 35/20 通过比较, 35/20 < 44/20 因此,Rahul 花的时间更少。 差值 = 44/20 - 35/20 = (44 - 35)/20 = 9/20 Rahul 比 Jaidev 少花9/20分钟。 下一主题六年级数学第八章 |
我们请求您订阅我们的新闻通讯以获取最新更新。