NCERT 10年级数学第14章解答：统计

练习 14.1

1. 一群学生在进行一项环保意识项目时，进行了一项调查，收集了以下关于一个地区20户家庭的植物数量的数据。求每户家庭的平均植物数量。

您使用了哪种方法来计算平均数，为什么？

解决方案

f_i 和 x_i 的值都比较小，所以我们使用直接法来计算平均数。

平均数 = x? =∑ f_ix_i/∑ f_i

= 162/20 = 8.1

每户家庭的平均植物数量 = 8.1

2. 考虑以下一家工厂50名工人每日工资的分布。

使用适当的方法计算该工厂工人的平均日工资。

解决方案

我们假设平均数为 A = 150。

组区间 = h = 上限 - 下限 = 20

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 150 + 20(-12)/50

= 145.2

工人的平均日工资 = 145.2 卢比

3. 以下分布显示了一个地区儿童的每日零用钱。平均零用钱为 18 卢比。求缺失频率 f。

解决方案

平均数 = x? = ∑f_ix_i/∑f_i = (752 + 20f)/(f + 44)

我们知道 x? = 18。因此

18 = (752 + 20f)/(f + 44)

18(f + 44) = 752 + 20f

18f + 792 = 752 + 20f

40 = 2f

f = 20

4. 在医院，医生检查了30名女性，并记录了她们每分钟的心跳次数，总结如下。选择一个合适的方法，计算这些女性的平均每分钟心跳次数。

解决方案

假设平均数为 A = 75.5

组距 = 上限 - 下限 = 3

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 75.5 + 3(4)/10

= 75.9

女性的平均每分钟心跳次数是 75.9

5. 在一个零售市场，水果商贩出售装在包装箱里的芒果。这些箱子包含不同数量的芒果。以下是按箱子数量划分的芒果分布。

求每个包装箱的平均芒果数量。您选择了哪种计算平均数的方法？

解决方案

给定的数据没有连续的组区间。因此，我们将给所有上限值加上 0.5，并从所有下限值减去 0.5。

给定的 f_i 值数值较大，所以我们将使用步进偏差法。

假设平均数为 A = 57

组距 = h = 上限 - 下限 = 3

真实平均数 = x? = A + h∑ f_id_i/∑ f_i

= 57 + 0.1875

= 57.19

每个包装箱的平均芒果数量是 57.19

6. 下表显示了一个地区25户家庭的每日食物支出。

使用合适的方法计算每日食物支出的平均值。

解决方案

假设平均数为 A = 225

组距 = h = 上限 - 下限 = 50

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 225 + 50(-7)/25

= 211

每日食物支出的平均值为 211 卢比。

7. 为了找出空气中 SO₂ 的浓度（以百万分之一，即 ppm 为单位），收集了某城市30个地区的有关数据，并如下呈现

计算空气中 SO₂ 的平均浓度。

解决方案

平均数 = x? = ∑ f_ix_i/∑ f_i

= 2.96/30

= 0.0986

空气中 SO₂ 的平均浓度为 0.0986 ppm。

8. 一位班主任记录了一个班级40名学生整个学期的缺勤情况。计算每名学生平均缺勤天数。

解决方案

平均数 = x? = ∑ f_ix_i/∑ f_i

= 499/40

= 12.48

学生平均缺勤天数为 12.48

9. 下表给出了35个城市的识字率（以百分比计）。计算平均识字率。

解决方案

假设平均数为 A = 70

组距 = 上限 - 下限 = 10

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 70 + 10(-2)/35

= 69.428

城市的平均识字率为 69.428 %

练习 14.2

1. 下表显示了一年中住进医院的病人的年龄

计算所给数据的众数和平均数。比较并解释这两种中心趋势度量。

解决方案

所给数据中的最高频率是 23。因此，众数组将是 35 - 45。

l = 35

f₁ = 23

f₂ = 14

f₀ = 21

组宽 = h = 10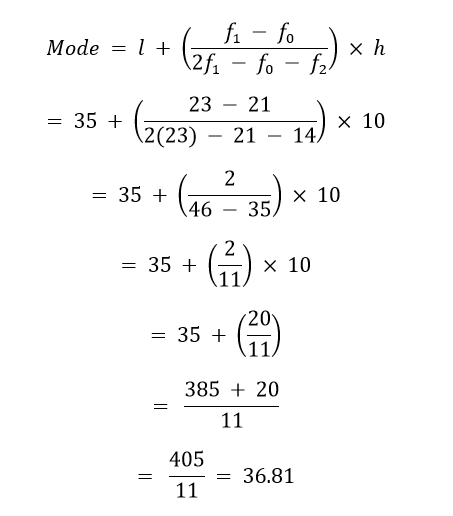

众数 = 36.81 岁

平均数 = x? = ∑ f_ix_i/∑ f_i

= 2830/80

= 35.375 岁

病人的平均年龄是 35.375 岁

2. 以下数据提供了225个电气元件的寿命（小时）信息

确定元件的众数寿命。

解决方案

所给数据中的最高频率是 61。因此，众数组将是 60 - 80。

l = 60

f₁ = 61

f₂ = 38

f₀ = 52

组宽 = h = 20

3. 以下数据给出了一个村庄200个家庭的总月家庭支出分布。求家庭的众数月支出。也求月支出的平均值

解决方案

所给数据中的最高频率是 40。因此，众数组将是 1500 - 2000。

l = 1500

f₁ = 40

f₂ = 33

f₀ = 24

组宽 = h = 500

假设平均数为 A = 2750

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 2750 + 500(-35)/200

= 2662.5

家庭的平均月支出 = 2662.5 卢比

4. 以下分布给出了印度高中教师与学生比例的地区分布。计算此数据的众数和平均数。解释这两种度量。

解决方案

所给数据中的最高频率是 10。因此，众数组将是 30 - 35。

l = 30

f₁ = 10

f₂ = 3

f₀ = 9

组宽 = h = 5

平均数 = x? = ∑f_ix_i/∑f_i

= 1022.5/35

= 29.214

州/联邦直辖区的平均师生比例 = 29.214

5. 给定的分布显示了世界上一些顶级板球运动员在一日国际板球比赛中得分。

计算数据的众数。

解决方案

所给数据中的最高频率是 18。因此，众数组将是 4000 - 5000。

l = 4000

f₁ = 18

f₂ = 9

f₀ = 4

组宽 = h = 1000

6. 一名学生记录了一个路口在100个每段3分钟的时段内经过的汽车数量，并将其总结在下表中。计算数据的众数

解决方案

所给数据中的最高频率是 20。因此，众数组将是 40 - 50。

l = 40

f₁ = 20

f₂ = 11

f₀ = 12

组宽 = h = 10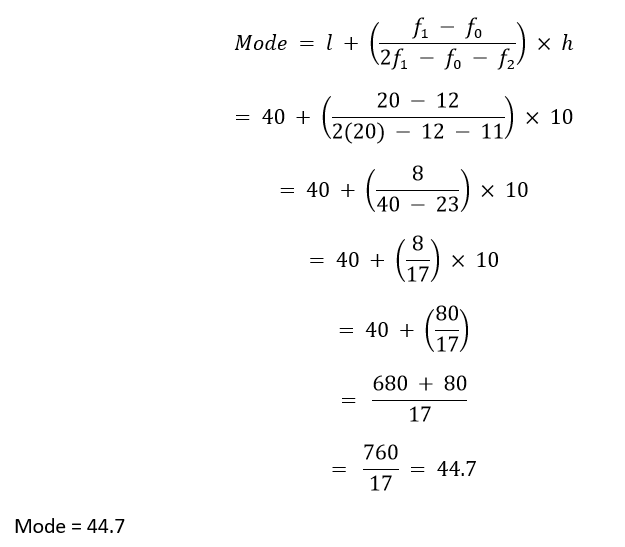

练习 14.3

1. 以下频率分布给出了一个地区68个消费者的月用电量。计算数据的中位数、平均数和众数，并进行比较。

解决方案

n = 68

n/2 = 34

因此，中位数类将是 125 - 145，累积频率为 42

l = 125

f = 20

cf = 22

组距 = h = 20

月用电量的中位数 = 137 单位

所给数据中的最高频率是 20。因此，众数组将是 125 - 145。

l = 125

f₁ = 20

f₂ = 14

f₀ = 13

组宽 = h = 20

众数 = 103.823

假设平均数为 A = 135

真实平均数 = x? = A + h∑ f_iu_i/∑ f_i

= 135 + 20(7)/68

= 137.06

月用电量的平均值是 137.06 单位。

通过比较数据的平均数、中位数和众数，我们可以得出它们彼此近似相等。

2. 如果下面分布的中位数是 28.5，求 x 和 y 的值。

解决方案

n = 60

n/2 = 30

因此，中位数类将是 20 - 30，累积频率为 25 + x

l = 20

f = 20

cf = 5 + x

组距 = h = 10

∑ f_i = 45 + x + y = n

45 + 8 + y = 60

53 + y = 60

y = 7

因此，x 和 y 的值分别为 8 和 7。

3. 一位人寿保险代理人发现了以下100名保单持有人的年龄分布数据。计算中位年龄，前提是保单仅授予年龄在18岁及以上但不到60岁的人。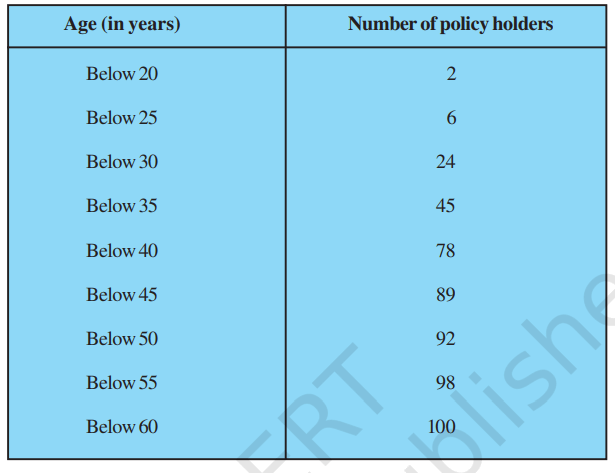

解决方案

n = 100

n/2 = 50

因此，中位数类将是 35 - 40，累积频率 = 78

l = 35

f = 33

cf = 45

组距 = h = 5

中位年龄 = 35.75 岁

4. 一种植物的40片叶子的长度已测量到最接近的毫米，并得到的数据如表所示

计算叶子的中位长度。

(提示：在计算中位数时，需要将数据转换为连续的组别，因为公式假定组别是连续的。组别然后变为 117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5。)

解决方案

由于数据不是连续的，我们将给所有上限值加上 0.5，并从所有下限值减去 0.5。

n = 40

n/2 = 20

因此，中位数类将是 144.5 - 153.5，累积频率为 29

l = 144.5

f = 12

cf = 17

组距 = h = 9

叶子的中位长度 = 146.25 毫米。

5. 下表显示了400个氖灯的寿命分布

计算灯泡的中位寿命。

解决方案

n = 400

n/2 = 200

因此，中位数类将是 3000 - 3500，累积频率为 216

l = 3000

f = 86

cf = 130

组距 = h = 500

灯泡的中位寿命 = 3406.976 小时

6. 从当地电话簿中随机抽取了100个姓氏，并获得了姓氏中英文字母数量的频率分布，如下所示

确定姓氏的中位数字母数量。计算姓氏的平均字母数量？也计算姓氏的众数组。

解决方案

n = 100

n/2 = 50

因此，中位数类将是 7 - 10，累积频率为 76

l = 7

f = 40

cf = 36

组距 = h = 3

字母的中位数数量 = 8.05

平均数 = x? = ∑ f_ix_i/∑ f_i

= 825/100 = 8.25

平均字母数量 = 8.25

所给数据中的最高频率是 40。因此，众数组将是 7 - 10。

l = 7

f₁ = 40

f₂ = 16

f₀ = 30

组宽 = h = 3

姓氏的众数字母数量 = 7.882

7. 下面的分布显示了一个班级30名学生体重的分布。计算学生的体重中位数。

解决方案

n = 30

n/2 = 15

因此，中位数类将是 55 - 60，累积频率为 19

l = 55

f = 6

cf = 13

组距 = h = 5

学生的体重中位数 = 56.667 千克

练习 14.4

1. 下面的分布给出了一个工厂50名工人的日收入。

将上述分布转换为“小于型”累积频率分布，并绘制其 ogive 曲线。

解决方案

我们需要将数据转换为“小于型”分布并计算累积频率。

使用上限和相应的累积频率，我们可以得到点 (120, 12), (140, 26), (160, 34), (180, 40), 和 (200, 50)。我们将绘制一个坐标图，并将这些点连接起来以获得“小于型”ogive 曲线。

2. 在对一个班级35名学生的体检过程中，记录了他们的体重如下

为给定数据绘制“小于型”ogive 曲线。然后从图表中得到中位体重，并通过公式验证结果。

解决方案

使用上限和相应的累积频率，我们可以得到点 (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32) 和 (52, 35)。我们将绘制一个坐标图，并将这些点连接起来以获得“小于型”ogive 曲线。

频率之和为 35。因此，我们将定位 y 轴或累积频率轴上的点 35/2 = 17.5。

通过点 (0, 17.5) 向 x 轴画一条平行线，直到它与 ogive 曲线相交。

在与 ogive 曲线相交的点处绘制垂直线。

该点的坐标发现为 (46.5, 17.5)。因此，根据给定数据，46.5 是学生的体重中位数。

验证

我们需要计算实际频率。

n = 35

n/2 = 17.5

因此，中位数类将是 46 - 48，累积频率为 28

l = 46

f = 14

cf = 14

组距 = h = 2

学生的体重中位数 = 46.5 千克

因此，学生体重的中位数已得到验证。

3. 下表给出了一个村庄100个农场的每公顷小麦产量。

将分布更改为“大于型”分布，并绘制其 ogive 曲线。

解决方案

我们需要将给定数据转换为“大于型”分布并找出累积频率。

使用上限和相应的累积频率，我们可以得到点 (50, 100), (55, 90), (60, 90), (65, 78), (70, 54) 和 (75, 16)。我们将绘制一个坐标图，并将这些点连接起来以获得“大于型”ogive 曲线。