NCERT 解决方案 六年级数学

第4章：基本几何概念

练习 4.1

1. 使用图形命名

(a) 五个点

答案：O、B、C、D、E

解释：点是确定位置的点。

(b) 一条直线

答案：DE、DO、DB、ED、EB

解释：两条线段组成一条直线。图中有多条直线。

例如：

OB, OE, OD, OC

DE, DO, DB

EO, ED, EB

(c) 四条射线

答案：ED、EB、DB、DE

解释：射线是一种直线，它在一个方向上无限延伸。

图中有多条射线。

OB, OE, OD, OC

DE, DO, DB

EO, ED, EB

(d) 五条线段

答案：ED、EB、DB、DE、OC

解释：图中有多条线段。

OB, OE, OD, OC

DE, DO, DB

EO, ED, EB

2. 用所给的四个字母，每次选两个字母，写出所有可能的（十二种）表示法来命名直线。

答案:

1. AB
2. AC
3. AD
4. BA
5. BC
6. BD
7. CA
8. CB
9. CD
10. DA
11. DB
12. DC

3. 使用图形命名

(a) 包含点 E 的直线。

答案：AE

解释：有几条包含点 E 的直线。

例如：

AE, BE, DE, FE

(b) 通过点 A 的直线。

答案：AE

解释：有几条通过点 A 的直线。

例如：

AE, AD, and AB

(c) 点 O 所在的直线

答案：OC 或 CO

解释：O 位于直线 OC 上，也称为 CO。

(d) 两对相交直线。

答案:

第一对：CO 和 AE

第二对：AE 和 EF

解释：相交直线的交点只有一个。

这些相交直线的两对有多种名称。

例如：

1.

OC and EA

EA and FE

2.

OC and AB

EF and DE

3.

OC and AD

FE and EB

4. 有多少条直线可以通过

(a) 一个给定的点？

答案：无数 / 数不清

解释：无数条直线可以穿过一个点。

(b) 两个给定的点？

答案: 1

解释：只有一条直线可以穿过两个给定的点。

5. 画一个粗略的图形，并按以下情况标记

(a) 点 P 在 AB 上。

图:

(b) XY 和 PQ 相交于 M。

图:

(c) 直线 l 包含 E 和 F，但不包含 D。

图:

(d) OP 和 OQ 在 O 点相交。

图:

6. 考虑直线 MN 的以下图形。根据给定图形判断以下陈述是真还是假。

(a) Q、M、O、N、P 都在直线 MN 上。

答案：真

解释：Q、M、O、N、P 都在直线 MN 上。Q 和 P 也都在直线 MN 上，

(b) M、O、N 都在线段 MN 上。

答案：真

解释：Q、M、O、N、P 都在线段 MN 上。

(c) M 和 N 是线段 MN 的端点。

答案：真

解释：线段由两个端点形成。它根据两个端点命名。因此，直线 MN 有两个端点 M 和 N。

(d) O 和 N 是线段 OP 的端点。

答案：假

解释：线段由两个端点形成。它根据两个端点命名。因此，直线 OP 有两个端点 O 和 P。

(e) M 是线段 QO 的一个端点。

答案：假

解释：直线 QO 有两个端点 O 和 Q。M 只是直线 QO 上的一个点，而不是端点。

(f) M 是射线 OP 上的一个点。

答案：假

解释：射线是直线的一个方向。射线 OP 不包含点 O，因为它们的方向相反。

(g) 射线 OP 不同于射线 QP。

答案：真

解释：射线 OP 包含点 O、P 和 N，而射线 QP 包含点 Q、M、O、N、P。

(h) 射线 OP 与射线 OM 相同。

答案：假

解释：射线 OP 包含点 O、P 和 N，而射线 OM 包含点 O 和 M。

(i) 射线 OM 与射线 OP 不相对。

答案：假

解释：射线 OM 与射线 OP 相对，因为它们的方向相反。

(j) O 不是 OP 的起点。

答案：假

解释：射线从一个起点开始。因此，O 是射线 OP 的起点。

(k) N 是 NP 和 NM 的起点。

答案：真

解释：射线从一个起点开始。因此，N 是射线 NP 和 NM 的起点。

练习 4.2

1. 将以下曲线分为（i）开放或（ii）封闭。

(a) 开放曲线

(b) 封闭曲线

(c) 开放曲线

(d) 封闭曲线

(e) 封闭曲线

说明:

开放曲线是指首尾不相连的曲线。这意味着曲线的端点没有连接在一起。

封闭曲线是指有开口端的曲线。这意味着曲线的端点是不同的。

2. 画粗略的图来说明以下内容

(a) 开放曲线

图:

(b) 封闭曲线。

图:

我们可以画任何类型的开放或封闭曲线。

3. 画一个多边形并涂上其内部。

多边形是由三个或更多线段组成的图形。有不同类型的多边形。

图:

说明:

1. 这是一个有六条边的多边形。
2. 这是一个有三条边的多边形。
3. 这是一个有五条边的多边形。

4. 考虑给定图形并回答问题

(a) 它是一条曲线吗？

答案：是

它是一条曲线，因为曲线是由首尾相连的线段组成的。

(b) 它是封闭的吗？

答案：它是一个封闭图形，因为上述图形的端点是首尾相连的。

5. 如果可能，用粗略的图来说明以下每一项

(a) 一个不是多边形的封闭曲线。

图:

说明:

(b) 一个完全由线段组成的开放曲线。

图:

说明:

曲线是由首尾相连的线段组成的。多边形是由三个或更多线段组成的封闭图形。曲线可以由不同类型的曲线和线段组成，而多边形仅由线段组成。

(c) 一个有两条边的多边形。

图:

不可能。我们无法用两条线段构成一个封闭图形。

解释：多边形是由三个或更多线段组成的封闭图形。

练习 4.3

1. 命名图中所示的角。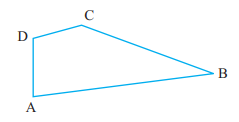

答案:

∠ADC 或 ∠D 或 ∠CDA

∠DCB 或 ∠C 或 ∠BCD

∠CBA 或 ∠B 或 ∠ABC

∠BAD 或 ∠A 或 ∠DAB

2. 在给定的图中，命名点（们），

(a) 在 ∠DOE 的内部

答案：点 A

解释：点 A 是 ∠DOE 内部（里面）唯一的一个点。

(b) 在 ∠EOF 的外部

答案：A、C、D

解释：点 A、C 和 D 位于 ∠EOF 的外部（外面）。

(c) 在 ∠EOF 上

答案：E、B、O、F

解释：点 E、B、O 和 F 位于角 ∠EOF 的边界上。

3. 画两个角，使它们有以下特征的粗略图

(a) 一个公共点。

图:

两个角：∠AOB 和 ∠DOC

公共点：O

(b) 两个公共点。

图:

两个角：∠AOB 和 ∠BOC

公共点：O、B

(c) 三个公共点。

图:

两个角：∠AOB 和 ∠BOC

公共点：O、B、D

(d) 四个公共点。

图:

两个角：∠AOB 和 ∠BOC

公共点：O、B、D、E

(e) 一条公共射线。

图:

两个角：∠AOB 和 ∠BOC

公共射线：OB

练习 4.4

1. 画一个三角形 ABC 的粗略草图。在其内部标记一个点 P，在其外部标记一个点 Q。点 A 在其外部还是内部？

图:

A 既不在外部也不在内部。

解释：点 A 位于三角形的边界上。因此，它既不在三角形的外部也不在内部。

2. (a) 识别图中的三个三角形。

答案：△ABC, △ADC, △ABD

(b) 写出七个角的名称。

答案：∠BAC, ∠ADB, ∠CAD, ∠BAD, ∠B, ∠C, ∠ADC

∠ABD 或 ∠DBA 或 ∠B

∠BDA 或 ∠ADB

∠ADC 或 ∠CDA

∠DCA 或 ∠ACD 或 ∠C

∠CAD 或 ∠DAC

∠DAB 或 ∠BAD

∠CAB 或 ∠BAC 或 ∠A

(c) 写出六条线段的名称。

答案：AB, BD, DC, AC, AD, BC

AB 或 BA

BD 或 DB

DC 或 CD

AC 或 CA

AD 或 DA

BC 或 CB

注意：角的名称、线段和三角形都可以顺时针或逆时针。我们可以选择任何选项。

(d) 哪个两个三角形有公共角 ∠B？

答案：△ABC, △ABD

练习 4.5

1. 画一个四边形 PQRS 的粗略草图。画出它的对角线。命名它们。对角线的交点在四边形的内部还是外部？

图:

对角线：PR、SQ

对角线交点：O

四边形的对角线交点位于三角形的内部。

解释：对角线总是在四边形的内部。因此，四边形的交点也位于其内部。

2. 画一个四边形 KLMN 的粗略草图。

图:

说明：

(a) 两对对边

答案:

KL 和 NM

KN 和 ML

(b) 两对对角

答案:

∠K 和 ∠M

∠L 和 ∠N

(c) 两对邻边

答案:

NM 和 LM

LK 和 KN

或

MN 和 NK

KL 和 NM

(d) 两对邻角

答案:

∠K 和 ∠L

∠M 和 ∠N

或

∠K 和 ∠N

∠M 和 ∠L

练习 4.6

1. 从图中识别

(a) 圆心

答案：O

O 是圆的圆心。

(b) 三条半径

答案：OC、OA、OB

OC、OA 和 OB 是圆的三条半径。

半径 = 直径/2

(c) 一条直径

答案：AC

直径总是通过圆心，并与圆周上的两点相切。因此，AC 是图中唯一的直径。

(d) 一条弦

答案：ED

弦是连接圆周上两点的线段。

(e) 两个内部点

答案：O、P

O 和 P 是位于圆内部的两个点。

(f) 一个外部点

答案：Q

Q 是位于圆外部的点。

(g) 一个扇形

答案：OAB

AOB 或 OAB 或 OBA

AOB 是圆的扇形。它由阴影部分表示。

(h) 一个弓形

答案：ED

ED 是圆的弓形。它也由阴影部分表示。

2.

(a) 圆的每一条直径都是弦吗？

答案：是

解释：圆上的弦是由连接其圆周或边界上的任意两点形成的。弦也可以通过圆心。因此，圆的每一条直径也是弦。

(b) 圆的每一条弦都是直径吗？

答案：圆上的弦是由连接其圆周或边界上的任意两点形成的。直径也通过圆心，而弦可以/不可以穿过圆心。因此，圆的每一条弦不总是直径。

3. 画任意一个圆并标记

(a) 它的圆心

O 是圆的圆心。

(b) 一条半径

OB 是圆的半径。

(c) 一条直径

AB 是圆的直径。

(d) 一个扇形

BOC 是圆的扇形。

(e) 一个弓形

DE 是圆的弓形。

(f) 内部一点

F 是圆内部的一点。

(g) 外部一点

G 是圆外部的一点。

(h) 一条弧

BC 是圆的弧。

4. 判断真假

(a) 圆的两条直径必然相交。

答案：真

解释：圆的每一条直径都通过圆心。因此，圆的两条直径必然相交。

(b) 圆心总是在其内部。

答案：真

解释：圆心表示位于其边界内的圆的中间点。因此，圆心总是在其内部。