11年级物理第2章 NCERT解决方案 - 单位和测量

学生可以使用这份11年级物理NCERT解决方案来更好地理解这个主题。11年级物理第2章单位和测量的最有用的学习材料是NCERT解决方案，它可以帮助学生掌握关键概念并在考试中取得好成绩。这些解决方案正确地提供了教科书问题的答案。

遵循最新的CBSE课程大纲2022-23，11年级物理NCERT解决方案的第2章主要有助于理解单位和测量的基础。我们日常生活中进行的许多事情都依赖于此。因此，学生必须很好地理解它。从早晨购买牛奶的磅数到早餐所需的面包磅数，再到午餐所需的米饭公斤数，一切都基于测量和单位。需要帮助理解本章重要概念的学生可以使用11年级物理NCERT解决方案。

NCERT解决方案 11年级物理第2章 单位和测量

练习：第35页

问题 2.1

填空。

1. 边长为1厘米的立方体的体积等于.....m³。
2. 半径为2.0厘米，高为10.0厘米的实心圆柱体的表面积等于....(mm)²。
3. 一辆以18公里/小时的速度行驶的车辆在1秒内行驶....米
4. 铅的相对密度为11.3。其密度为....g cm^-3或....kg m^-3。

答案

a.) 立方体体积 = (边长)³

(1 cm)³

= (1 × 10^-2 m)³

= 1 × 10^-6 m

b.) 已知：

r = 2 cm = 20 mm

h = 10 cm = 100 mm

总表面积，

S = 2πrh + 2πr²

S = 2πr(h + r)

S = 2 × 3.14 × 20(100+20)

S = 125.6 × 120

S = 15072 mm²

c.) 车辆速度 = 18 km/h

1 公里 = 1000 米

1 小时 = 60 x 60 = 3600 秒

车辆在1秒内行驶的距离 = 5 米

d.) 已知铅的相对密度 = 11.3

我们知道：

问题 2.2

通过适当的单位换算填空。

1. 1 kg m² s^-2 = ....g cm² s^-2
2. 1 m = ..... ly
3. 3.0 m s^-2 = .... km h^-2
4. G = 6.67 × 10^-11 N m² (kg)^-2 = .... (cm)³ s^-2 g^-1

答案

a.) 我们知道：

1 kg = 1000 g

1 米 = 100 厘米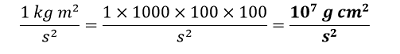

b.) 我们知道：

c.) 我们知道：

1 公里 = 1000 米

1 小时 = 3600 秒

d.) 已知：

G = 6.67 × 10^-11 N m² (kg)^-2

N = kg m s^-2

1 kg = 1000 g

1 米 = 100 厘米

问题 2.3

卡路里是热量（能量传递）的单位，约等于4.2 J，其中1J =1 kg m² s。假设我们采用一种单位制，其中质量单位等于α kg，长度单位等于β m，时间单位是γ s。证明卡路里以新单位表示的量值为4.2 α-1 β-2 γ2。

答案

1 卡路里 = 4.2 J = 4.2 kg m² s^-2

问题 2.4

清楚地解释这个陈述

“在没有指定比较标准的情况下，说一个量纲数量‘大’或‘小’是没有意义的”。鉴于此，请在必要时重述以下陈述。

1. 原子是极小的物体
2. 喷气式飞机以很高的速度行驶
3. 木星的质量非常大
4. 这个房间里的空气包含大量分子
5. 质子比电子的质量大得多
6. 声速远小于光速。

答案

与同类型的其他标准物品相比，一个物体被称为巨大或渺小。例如，就尺寸而言，船远大于自行车。以下是对其重述短语的比较：

1. 网球比原子大得多。
2. 与自行车相比，喷气式飞机的速度很高。
3. 将木星的质量与基本摆锤的质量进行比较，木星的质量要大得多。
4. 横向比较，房间里的空气分子数量比小盒子里多。
5. 篮球和棒球质量的差异可以用来衡量质子比电子重多少。
6. 与自行车和汽车速度的差异相比，声速远小于光速。

问题 2.5

选择一个新的长度单位，使得真空中的光速为1。如果光需要8分钟20秒才能覆盖这个距离，那么太阳到地球的距离是多少（以新单位表示）？

答案

我们想确定太阳到地球的距离，并且我们知道真空中的光速为1。

我们知道：

问题 2.6

以下哪种是测量长度最精确的设备？

1. 游标卡尺，滑尺上有20个刻度
2. 千分尺，螺距为1毫米，圆尺上有100个刻度
3. 可以测量到光波长以内长度的光学仪器

答案

选项 C 是正确答案。

读数最小时的设备被认为是最精确的设备

a.) 游标卡尺

它在滑尺上有20个刻度

b.) 千分尺

它在圆尺上有100个刻度，螺距为1毫米

c.) 光学仪器

在光波长内

光波长是多少？ 589 纳米

我们可以得出结论，光学仪器是测量长度最精确的工具。

问题 2.7

一名学生通过显微镜（放大倍数为100倍）测量人发的厚度。他进行了20次观察，发现显微镜视野中头发的平均宽度为3.5毫米。头发的厚度估计是多少？

答案

已知放大倍数为100，

显微镜视野中的头发通常为3.5毫米宽。

实际估计的发束厚度等于平均视野宽度乘以100乘以放大倍数，或3.5毫米/0.035毫米。

估计的发束厚度为0.035毫米，答案是

问题 2.8

回答以下问题

1. 给你一根线和一把米尺。你将如何估算线的直径？
2. 千分尺的螺距为1.0毫米，圆尺上有200个刻度。你认为可以通过增加圆尺上的刻度数来任意提高千分尺的精度吗？
3. 用游标卡尺测量薄黄铜棒的平均直径。为什么一组100次直径测量比仅5次测量能得到更可靠的估计？

答案

a.) 首先，将线缠绕在一个圆柱形线圈上，线圈绕组彼此紧密接触。一旦线圈完全缠绕好，就测量线圈绕组区域的长度。

设 l 表示线圈绕组部分的长度，n 表示线圈的缠绕圈数。

线的直径可以使用以下公式计算：

d = 缠绕线圈的长度乘以圈数，或 l × n

b.) 已知圆尺上有200个刻度，千分尺的螺距为1.0毫米。

仪器的精度越高，其读数越小。

千分尺的读数定义为：

读数= 螺距 / 刻度数

根据上述关系，随着刻度数的增加，读数的值会减小。因此，千分尺的精度会提高。然而，刻度数的增加只能达到某个点，之后再增加圆尺上的刻度就变得困难了。因此，通过增加圆尺上的刻度数，可以任意提高千分尺的精度。

c.) 可靠性描述了测量精度的程度。随着测量次数的增加，可靠性也会增加。这是因为大量测量中的随机误差的可能性远小于少量观测中的随机误差的可能性。因此，100次直径测量集比5次测量集更可靠。

问题 2.9

一张房屋照片占据35毫米幻灯片上的1.75平方厘米面积。将幻灯片投影到屏幕上，屏幕上的房屋面积为1.55平方米。投影仪-屏幕组合的线性放大倍数是多少？

答案

已知：

幻灯片上的房屋面积为= 1.75 cm²

在屏幕上形成的房屋图像面积为= 1.55 cm²

我们知道 1 m = 100 cm = 10² cm

因此，

在屏幕上形成的房屋图像面积为= 1.55 cm^{2 × 104 cm2}

面积放大倍数，

问题 2.10

说明以下数字的有效数字位数

1. 0.007 m²
2. 2.64 × 10²⁴ kg
3. 0.2370 g cm^-3
4. 6.320 J
5. 6.032 N m^-2
6. 0.0006032 m²

答案

数字的有效数字是那些通过具有意义的数字增加其测量分辨率的数字。这包括所有数字，除了

1.) 所有前导零

2.) 仅用作指示数字大小的尾随零（确切规则在识别有效数字中解释）

3.) 引入的虚假数字，例如，通过比原始数据精度更高的计算获得的，或者设备支持的精度更高的报告的测量值。

a.) 0.007 = 7 × 10^-3

有效数字是7。因此只有1个有效数字。

b.) 有效数字的个数是3

c.) 每个非零数字都具有意义。出现在非零数字之前的任何零都没有意义。出现在数字末尾并且紧接在小数点右侧的任何零都具有意义。在这个数字中，小数点前的零是唯一没有意义的数字。

因此，有4个有效数字。

d.) 每个非零数字都具有意义。出现在数字末尾并且紧接在小数点右侧的任何零都具有意义。

因此，有4个有效数字。

所有数字都具有意义（没有前导零和尾随零）。

有效数字的个数= 4

f.) 有效数字：6032

有效数字的个数= 4

问题 2.11

一块矩形金属板的长、宽、厚分别为4.234米、1.005米和2.01厘米。给出该板的面积和体积（以正确的有效数字表示）。

答案

A = 2 × (L × B + B × T + T × L)

∴A = 2 × (4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)

∴A = 2 × (4.2552 + 0.0202 + 0.0851)

∴A = 8.721 m²

∴A = 8.721 m² （以正确的有效数字表示）

V = L × B × T

∴V = 4.234 × 1.005 × 0.0201

∴V = 0.0855 m³ （以正确的有效数字表示）

问题 2.12

杂货店用天平测得的盒子质量为2.30千克。向盒子中添加两块质量分别为20.15克和20.17克的金块。请问

1. 盒子的总质量，
2. 金块质量的差值（以正确的有效数字表示）？

答案

m_i = 2.300 kg （两位有效数字）

m₁ = 20.15 g （四位有效数字）

m₂ = 20.175 g （四位有效数字）

a.) 相加：

最终质量不应超过2位有效数字，因为初始质量至少有2位有效数字。

因此 M = 2.3 kg

b.) 相减

m₂ - m₁ = 0.02 g

由于原始质量有四位有效数字，结果也可以有四位或更少。

所以，在这种情况下，有两位有效数字。

问题 2.13

一个物理量P与四个可观测值a, b, c和d的关系如下：

a, b, c和d的测量百分比误差分别为1%、3%、4%和2%。那么P的百分比误差是多少？如果使用上述关系计算出的P值为3.763，则结果应四舍五入到哪个值？

答案

已知：

P的百分比误差为13%

P的值为3.763

将数值四舍五入到两位正确小数位，得到答案3.8。

问题 2.14

一本印刷错误很多的书包含四种不同的位移y公式，用于描述粒子进行的某种周期性运动（a =粒子最大位移，v =粒子速度，T =运动周期）。根据量纲排除错误的公式。

(a =粒子最大位移，v =粒子速度，T =运动周期)。根据量纲排除错误的公式。

答案

由于所有方程的主题都是粒子的位移，因此长度应该是所有方程中的一个量纲。

现在，验证所有位移方程在量纲上是否准确。

这里，a是振幅，它具有长度量纲。该方程是准确的，因此。

b.) 我们知道vt应该是无量纲的，因为三角函数也是无量纲的。

vt = (LT^-1)(T) = L = [M⁰L¹T⁰]

因此，给定的方程是错误的。

因此，它在量纲上也是不准确的。

因此，它在量纲上也是不准确的。

问题 2.15

物理学中有一个著名的关系，它将粒子的“运动质量”m与“静止质量”mo联系起来，用其速度v和光速c表示（这个关系最初是由于阿尔伯特·爱因斯坦的狭义相对论而产生的）。一个男孩几乎正确地记住了这个关系，但忘记了常数c应该放在哪里。他写道：>

猜测 missing c 应该放在哪里。

答案

问题 2.16

原子尺度上方便的长度单位称为埃（angstrom），用Å表示：1 Å = 10^-10 m。氢原子的尺寸约为0.5 Å。一摩尔氢原子的总原子体积（以m³为单位）是多少？

答案

已知：

问题 2.17

一摩尔理想气体在标准温度和压力下体积为22.4升（摩尔体积）。摩尔体积与一摩尔氢的原子体积之比是多少（取氢分子的大小约为1 Å）？为什么这个比率如此之大？

答案

已知：

由于氢气中的原子间距很高，因此比率非常大。

问题 2.18

清楚地解释这个常见的观察现象：如果你看向一辆快速行驶的火车窗外，附近的树木、房屋等似乎以与火车运动相反的方向快速移动，但远处的物体（山顶、月亮、星星等）似乎是静止的（事实上，由于你知道自己在移动，这些远处的物体似乎与你一起移动）。

答案

视线是指连接物体和观察者眼睛的假想路径。当火车行驶时，视线会发生剧烈变化，这使得附近的静止物体，如房屋、树木和其他建筑物，似乎在相反的方向快速移动。

然而，由于距离很远，远处的物体，如树木、星星和其他天体，似乎是静止的。因此，视线不会快速改变其路径。

问题 2.19

第2.3.1节中的“视差”原理用于确定非常遥远恒星的距离。基线AB是连接地球在其绕日轨道上相隔六个月的两个位置的直线。也就是说，基线大约是地球轨道的直径？3 × 10¹¹米。然而，即使最近的恒星也非常遥远，以至于如此长的基线，它们显示的视差也只有大约1弧秒（秒）左右。秒差距（parsec）是在天文尺度上方便的长度单位。它是指一个物体从基线两端（基线等于地球到太阳的距离）显示1弧秒（秒）视差的距离。一秒差距等于多少米？

答案

地球轨道的直径= 3 × 10¹¹ 米

地球轨道的半径 r = 1.5 × 10¹¹ 米

设恒星的视差角为 θ = 1″ (s) = 4.847 × 10^-6 弧度。

设恒星的距离为 D。

秒差距定义为平均地球轨道半径为一个1″角张成的距离

因此，

因此 1 秒差距？ 3.09 × 10¹⁶ 米。

问题 2.20

离我们太阳系最近的恒星是4.29光年。这个距离相当于多少秒差距？当从地球绕太阳轨道上相隔六个月的两个位置观察时，这颗恒星（名为Alpha Centauri）会显示出多大的视差？

答案

光一年所传播的距离称为光年。

因此，

光速= (3× 10⁸) m/s

时间= 1 年= (365 × 24 × 3600)秒

因此，

问题 2.21

精确测量物理量是科学的需要。例如，要确定飞机的速度，必须有一种准确的方法来查找其在相隔极短时间间隔的位置。这实际上是第二次世界大战期间雷达发现的动机。设想现代科学中需要精确测量长度、时间、质量等的不同例子。另外， wherever you can, give a quantitative idea of the precision needed.

答案

科学必须使用精确的仪器来获取精确的测量。精确测量对于几个操作是必需的。

在放射成像技术中使用精密仪器来测量单个原子之间的空间。例如，在中子与放射性中子碰撞的精确时刻，会发生核反应。使用超短激光脉冲可以确定几个化学反应所需的时间。

问题 2.22

正如科学中需要精确测量一样，能够使用基本概念和日常观察进行粗略估计也非常重要。思考一下如何估计以下量（如果一个量难以获得估计值，则尝试得到该数量的上界）。

1. 季风期间印度上空的载雨云的总质量
2. 一头大象的质量
3. 风暴期间的风速
4. 你头上头发丝的数量
5. 你教室里空气分子的数量。

答案

a.) 假设在季风季节，气象学家在印度记录的平均降雨量为100厘米。

h=100厘米=1米

印度面积= A=3.3× 10¹² m²

水的密度= 1000 kg/m³。

载雨云的质量

m=ρAh

m=载雨云的质量

ρ = 水的密度

A= 印度面积

h=记录的平均降雨量

代入数值，我们得到，

m = 1000 × 3.3 × 10¹² ×1

= 3.3 × 10¹⁵kg

因此，载雨云的质量为3.3× 1¹⁵kg。

b.) 让我们先考虑一艘漂浮在水中的空船。那么在这种情况下，会有某种程度的水位移被空船取代。在这种情况下，空船排开的水的体积将写为V₁=Ad₁

V₁= 空船排开的水的体积。

A= 船的底面积。

d₁= 船浸入水中的深度。

现在将大象移到空船里，然后测量船在水中的新深度。载有大象的船排开的水的体积将由V₂=Ad₂给出

V₂= 载有大象的船排开的水的体积。

d₁= 载有大象的船浸入水中的深度。

现在大象排开的水的体积是

V = V₂ - V₁

= Ad_{2 - Ad1}

= A(d₂ - d₁)

大象的质量

m=ρV

= ρA(d₂ - d₁)

c.) 可以使用充气气球来估算风暴期间的风速。气体必须比空气轻，因此气球会漂浮在空中。下图显示了在风暴期间测量风速所需的设备。

气球的位置A是无风时的位置，气球的位置B是风吹并使气球偏离其原始位置时的位置。

通过知道d的值，可以计算风暴的速度。

还可以使用风速计来计算风速。吹来的风会转动风速计，风速计每分钟的转数可以提供风暴期间风速的信息。

人头半径= 8 × 10^-2米

人发厚度= 5 × 10^-5米

头发丝的数量，

n = AHah =π R² πt² = (Rt)²

n=头发丝的数量

R=头半径

t=头发厚度

代入数值，

n =(8× 10^-2 × 5 × 10^-5)²

= 2.56× 10⁶

e.) 例如，我们取一个长10米，宽8米，高4米的教室。

教室的体积V将是，

V = lbh

V = 教室的体积。

l = 教室的长度。

b = 教室的宽度。

h = 教室的高度。

代入数值，我们得到，

V = 10 × 8 × 4 = 320m³

因此，22.4× 10^-3 m³的空气含有6.02× 10²³个空气分子。

所以教室中存在的分子数量，

n = 6.02 × 10²³× 22.4 × 10^-3 × V

代入数值，我们得到，

n = 6.02 × 10²³ × 22.4 × 10^-3 × 320 = 8.6× 10²⁷

问题 2.23

太阳是一个炽热的等离子体（电离物质），其内核温度超过10⁷ K，外表面温度约为6000 K。在这些高温下，没有任何物质保持固态或液态。你预计太阳的质量密度范围是多少，是固液密度范围还是气态密度范围？根据以下数据检查你的猜测是否正确：太阳质量= 2.0 × 10³⁰ kg，太阳半径= 7.0 × 10⁸ m。

答案

质量= 2 x 10³⁰ kg

半径= 7 x 10⁸ m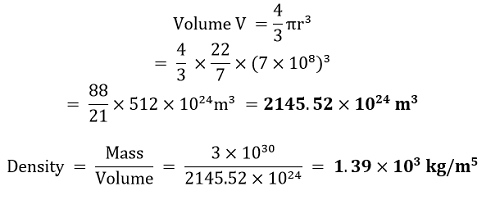

密度介于液体和固体之间。由于太阳内层的强大引力作用于外层，因此其密度很大。

问题 2.24

当行星木星与地球的距离为8.247亿公里时，其角直径测量为35.72英寸。计算木星的直径。

答案

木星与地球之间的距离, D= 824.7 百万公里 = 824.7 x 10⁶ km

角直径 θ = 35.72"

= 35.72 x 4.85 x 10^-6 弧度
= 173.242 x 10^-6 弧度

木星的直径，

d = θ x D

= 173.241 x 10^-6 x 824.7 x 10⁶ km

=142871

= 1.43 x 10⁵ km

附加练习

问题 2.25

一个快步雨中行走的人，速度为v，必须向前倾斜雨伞，使其与垂直方向成 θ 角。一个学生推导出了 θ 和 v 之间的关系：tan θ = v，并检查该关系是否具有正确的极限：当 v →0 时，θ →0，正如预期的那样（我们假设没有强风，并且对于静止的人来说，雨是垂直落下的）。你认为这个关系正确吗？如果不正确，请猜测正确的关系。

答案

遵循量纲方程的齐次性原理，
LHS的量纲 = RHS的量纲

这里给出的关系是 v = tan θ。

由于 tan θ 是一个三角函数，所以它基本上是无量纲的。v的量纲也是[L¹ T^-1]。

所以我们可以说给定的关系是不正确的。

如果我们用雨的速度u除以LHS，我们可以使关系正确。这样做后，关系变为

这个方程在量纲上是正确的。

问题 2.26

据称，两个铯钟在不受任何干扰的情况下运行100年后，可能仅相差约0.02秒。这对于标准铯钟测量1秒时间间隔的精度意味着什么？

答案

总时间= 100 年= 100 x 365 x 24 x 60 x 60 秒

100年内的误差= 0.02 秒
1秒内的误差，

问题 2.27

估计一个钠原子的平均质量密度，假设其尺寸约为2.5 Å（使用已知的阿伏伽德罗数和钠的原子质量）。将其与钠在晶体相中的质量密度进行比较：970 kg m^-3。这两个密度是否属于同一数量级？如果是，为什么？

答案

钠直径= 2.5 A = 2.5 x 10^-10 米

因此，半径为1.25 x 10^-10米

钠原子的体积，

固态钠的密度约为4669.2 kg m^-3，而晶体形式的密度为970 kg m^-3。因此，它们属于不同的数量级。固态时原子堆积得更紧密，而在晶体形式中，原子形成序列，有时会形成空隙或为空。因此，固态密度比晶体相大。

问题 2.28

核尺度上方便的长度单位是费米：1 f = 10^-15 m。核尺寸大致遵循以下经验关系：

r = r₀A^1/3

其中 r 是原子核的半径，A 是其质量数，r₀ 是一个常数，约等于1.2 f。证明该规则意味着不同原子核的核质量密度几乎是恒定的。估计钠原子核的质量密度。将其与练习2.27中获得的钠原子的平均质量密度进行比较。

答案

原子核的半径

因此，核质量密度比练习2.27中获得的钠原子的原子质量密度大得多。

问题 2.29

激光是一种非常强烈、单色、单向的光束源。激光的这些特性可以用来测量长距离。激光已经非常精确地确定了月球到地球的距离。一束激光照射到月球，返回反射后需要2.56秒。月球绕地球轨道的半径是多少？

答案

激光束从月球表面反射后返回地球所需的时间= 2.56 秒

激光速度 c = 3 x 10⁸ m/s。

设 d 为月球到地球的距离，

激光信号到达月球所需的时间，

问题 2.30

声纳（声音导航和测距）使用超声波来探测和定位水下物体。在一艘配备声纳的潜艇中，探测波的产生与其从敌方潜艇反射后回波的接收之间的时间延迟为77.0秒。敌方潜艇的距离是多少？（水中声速= 1450 m/s）。

答案

水中声速, v = 1450 m s^-1

从回波产生到其在反射后被接收的时间间隔, 2t= 77.0 秒

声波到达潜艇所需的时间，

问题 2.31

我们现代天文学家发现的宇宙中最遥远的天体如此之远，以至于它们发出的光需要数十亿年才能到达地球。这些天体（称为类星体）具有许多令人费解的特征，这些特征尚未得到令人满意的解释。一个类星体发出的光需要30亿年才能到达我们，它到地球的距离是多少公里？

答案

类星体光到达观测者所需的时间, t = 3.0 十亿年 = 3.0 x 10⁹ 年 = 3.0 x 10⁹ x 365 x 24 x 60 x 60 秒

= 94608000 x 10⁹ 秒

= 9.46 x 10¹⁶ 米

光速= 3 x 10⁸ m/s

类星体到地球的距离= 3.0 x 10⁸ x 9.46 x 10¹⁶ 米

= 28.38 x 10²⁴ 米

问题 2.32

这是一个众所周知的事实，在日全食期间，月球的圆盘几乎完全覆盖了太阳的圆盘。根据这一事实以及您从示例2.3和2.4中收集到的信息，确定月球的大致直径。

答案

从示例2.3和2.4中，我们得到以下数据

月球到地球的距离= 3.84 x 10⁸ 米

太阳到地球的距离= 1.496 x 10¹¹ 米

太阳直径= 1.39 x 10⁹ 米

太阳的角直径, θ = 1920″ = 1920 x 4.85 x 10^-6 弧度 = 9.31 x 10^-3 弧度

[1″ = 4.85 x 10^-6 弧度]

太阳和月亮的角直径必须相似，因为在日全食期间，月球的圆盘会完全遮挡太阳的圆盘。

月亮的角直径, θ = 9.31 x 10^-3 弧度

地月距离, S = 3.8452 x 10⁸ 米

因此，月亮的直径，

D = θ × S

= 9.31× 10^-3 × 3.8452 × 10⁸ 米

= 35.796 × 10⁵ 米