二元决策树

二叉决策树是一种决策图，它遵循从根节点开始并以叶节点结束的顺序。叶节点代表我们希望通过决策实现的结果。它直接受到二叉树的启发。由于二叉树中每个节点最多可以有两个节点，同样，在每一步中，我们有一个或两个步骤，我们将在其中选择一个。

当数据量很大且我们希望在每一步处理后获得结果时，它是一种用于机器学习的决策算法。

如果没有适当的约束，决策树可能会扩展，直到每个节点只包含一个样本（或非常少的样本）。由于这种情况，模型变得过拟合并失去了准确泛化的能力。通过使用一致的测试集、交叉验证和最大允许深度可以避免这个问题。类平衡是另一个需要考虑的关键因素。当一个类占主导地位时，决策树可能会产生不准确的结果，因为它们对不平衡的类很敏感。可以使用重采样技术之一，或 scikit-learn 实现提供的类权重选项来缓解此问题。通过避免偏差，可以按比例惩罚占主导地位的类。

假设在一个数据集中，我们有 n 个数据点，每个点有 m 个特征。那么决策树可能看起来像这样，其中 t 是阈值

单分裂节点

因此，在二叉决策树中，每个节点都应该以这样一种方式选择，即我们为该节点选择的特征应该能够以最佳方式分离数据。如果我们选择这样的节点，它会减少步骤数，并且我们可以在更少的步骤和更低的复杂性下获得目标。

在现实生活中，选择或找到一个能最小化二叉决策树结构的特征是非常困难的。树的结构取决于我们选择的特征和阈值。

例如：我们有一个学生班级，所有男生都有黑发，女生都有绿发。黑发的学生有不同的长度，红发的学生也有不同的长度。如果我们的目标是获取黑发和绿发的数据组成，那么一个简单的二叉决策树可能看起来像这样

在上面的树中，我们根据头发长度进行划分，然后根据发色进行划分。由于我们不需要根据头发长度进行分离，所以这被称为杂质。杂质节点被添加到树中，这不必要地使结构更大更复杂。如果杂质节点在目标节点下方，则没有问题。

所以我们可以得到上面例子中的最优树，像这样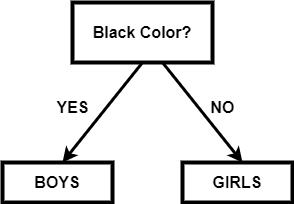

如果我们需要关于头发长度的数据，那么这个节点可以很容易地添加到叶节点下方。

注意：所以，每个节点的选择可以用以下形式表示

在上面的等式中，我们有两个值，其中 i 表示我们想要分割的数据集的索引。在根节点中，我们将有一个完整的数据集，所以 i 将为零，在后续步骤中，数据集将减少。t_k 表示我们分割数据集的阈值。所以我们在选择阈值时必须非常小心，因为阈值决定了树的结构。如果我们的阈值不好，那么我们可能需要一棵很长的树才能达到目标。

我们可以测量总杂质，我们的目标将是尽快减少总杂质以达到期望的节点。

我们可以通过以下公式获得总杂质度量

这里 D 代表我们正在处理的完整数据集。D_left 和 D_right 代表根据阈值分割后创建的左节点和右节点数据集。

I 代表节点的总杂质度量。