C++ 最近点对

2025年2月11日 | 阅读 7 分钟

引言

计算几何中的一个主要问题是最近点对问题：给定平面上的一组点，找出最近的两个点。这个问题在现实生活中非常有用，例如，在空中交通管制中，识别和跟踪相互靠近的飞机以防止碰撞非常重要。最近点对问题也可以用不同的方法和不同的时间复杂度来解决。

已经提到的穷举法，通过计算每对点之间的距离并选择最小距离来工作，其时间复杂度为 ο(n2)。然而，后来开发了遵循分治策略的更优算法，算法的时间复杂度降低到 О(n log n)。

本文将重点介绍如何在 C++ 中解决最近点对问题：穷举法和分治法。我们将解释这些方法的原理，并 along with 代码示例描述过程的每一步。

数学背景

最近点对问题要求确定欧几里得平面上给定点集中相互最接近的两个点。这个问题通过几何知识、距离度量和算法复杂度涉及数学。在这项工作中，讨论了这些方面的特征，以简要介绍它们。

欧几里得距离

在 2D 平面上，两个点 p= (p_x,p_y) 和 q= (q_x,q_y) 之间的欧几里得距离由以下公式给出：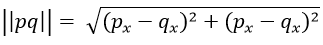

这称为距离公式，它源自勾股定理，即两点之间的距离是构成第一组坐标和第二组坐标之间差值的直角三角形的斜边长度。

暴力破解法

在计算最近点对问题时，穷举法通过计算每对可能点之间的距离，然后找到最小距离来解决。此方法的O(n^2)时间复杂度，其中n是点的数量。这是因为有 n(n-1)/2 对可能点。

分治法

为了提高穷举法的效率，我们使用分治法，它将时间复杂度降低到 Ο(n log⁡ n)。该方法包括以下步骤：

排序点：首先，按 x 坐标对点进行排序，此步骤的时间复杂度为 Ο(n log⁡ n)。
划分：然后，将点集分成两半。这是通过通过中值点（按 x 坐标）绘制一条垂直线来完成的。
解决：递归地找到左半部分和右半部分中的最小距离。
合并：比较左右两半点之间的最小距离。此外，还会检查靠近分割线的点（在迄今为止找到的最小距离范围内），以查看是否有任何跨越线的点对具有更小的距离。

C++ 实现最近点对的程序

 
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <limits>

// Structure to represent a point in 2D plane
struct Point {
    int x, y;
};

// Function to compare points by their x-coordinates
bool compareX(const Point& a, const Point& b) {
    return a.x < b.x;
}

// Function to compare points by their y-coordinates
bool compareY(const Point& a, const Point& b) {
    return a.y < b.y;
}

// Function to calculate the distance between two points
double distance(const Point& p1, const Point& p2) {
    return sqrt((p1.x - p2.x) * (p1.x - p2.x) + 
                (p1.y - p2.y) * (p1.y - p2.y));
}

// A utility function to find the distance between the closest points in strip of given size. All points in strip[] are sorted according to y coordinate.
double stripClosest(std::vector<Point>& strip, double d) {
    double min_dist = d; // Initialize the minimum distance as d

    std::sort(strip.begin(), strip.end(), compareY); // Sort the points according to Y coordinates

    // Pick all points one by one and try the next points till the difference between y coordinates is smaller than d.
    for (size_t i = 0; i < strip.size(); ++i) {
        for (size_t j = i + 1; j < strip.size() && (strip[j].y - strip[i].y) < min_dist; ++j) {
            if (distance(strip[i], strip[j]) < min_dist) {
                min_dist = distance(strip[i], strip[j]);
            }
        }
    }

    return min_dist;
}

// A recursive function to find the smallest distance
double closestUtil(std::vector<Point>& points, size_t left, size_t right) {
    // If there are 2 or 3 points, then use brute force
    if (right - left <= 3) {
        double min_dist = std::numeric_limits<double>::max();
        for (size_t i = left; i < right; ++i) {
            for (size_t j = i + 1; j < right; ++j) {
                if (distance(points[i], points[j]) < min_dist) {
                    min_dist = distance(points[i], points[j]);
                }
            }
        }
        return min_dist;
    }

    // Find the middle point
    size_t mid = left + (right - left) / 2;
    Point midPoint = points[mid];

    // Consider the vertical line passing through the middle point
    // Calculate the smallest distance in the left and right halves
    double dl = closestUtil(points, left, mid);
    double dr = closestUtil(points, mid, right);

    // Find the smaller of the two distances
    double d = std::min(dl, dr);

    // Build an array strip[] that contains points close to the line passing through the middle point
    std::vector<Point> strip;
    for (size_t i = left; i < right; ++i) {
        if (std::abs(points[i].x - midPoint.x) < d) {
            strip.push_back(points[i]);
        }
    }

    // Find the closest points in strip. Return the minimum of d and the closest distance in strip[]
    return std::min(d, stripClosest(strip, d));
}

// The main function that finds the smallest distance
double closest(std::vector<Point>& points) {
    std::sort(points.begin(), points.end(), compareX); // Sort the points according to X coordinates
    return closestUtil(points, 0, points.size());
}

int main() {
    std::vector<Point> points = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}};
    std::cout << "The smallest distance is " << closest(points) << std::endl;
    return 0;
}   

输出

 
The smallest distance is 1.41421

最近点对问题的应用

最近点对问题在各个领域都有许多实际应用。以下是一些主要应用：

空中交通管制
碰撞检测：在空中交通管制中，控制物体（例如飞机）飞行时的距离至关重要，以防止它们发生碰撞。因此，利用计算飞机最近对的算法的思想，可以确定现有的邻近性并发出信号来分离飞机，从而防止极其危险的情况。
天文学
识别星团：在保持恒星或星系中的邻近关系时，天文学家会应用最近点对算法。科学家通过检查恒星距离来发现最近的邻居，从而揭示恒星形成的模式和其他相关现象。
地理信息系统 (GIS)
最近邻搜索：有时应用程序需要找到一组最近的对象，例如，找到给定坐标最近的医院或设置最近的兴趣点。这涉及到路线规划、资源提供和任何意外事件的发生。
计算机图形学
模拟中的碰撞检测：在计算机图形学和计算机模拟中，碰撞检测对于对象之间的交互方式至关重要。最近点对算法可用于计算对象何时接触的计算；这在物理模拟、游戏和虚拟现实中特别有用。
机器人技术
路径规划：当机器人穿行于环境中时，它们应该避开前方的物体，并寻求最短可能的路径。利用最近点对算法，机器人可以轻松识别附近的物体和不会对其造成危险的路径，从而进一步提高机器人穿越复杂区域的导航能力。
聚类和分类
数据分析：事实上，最近点对算法在机器学习和数据挖掘方法中得到了应用，特别是在聚类模型中，包括层次聚类。因此，算法可以通过使用两点之间的最短距离将相似的项目组合在一起，这可能有助于识别模式、检测异常和细分客户。
网络
传感器网络：无线传感器网络特别突出了测量不同节点之间距离的潜力，以便在与传感器通信时检查覆盖范围。最近点对算法可用于放置传感器和发现可能的连接问题。
医学影像
分析生物结构：在医学影像中，最近点对可以用来确定不同生物构造的连接程度。这对于识别肿瘤等目的很有用，其中细胞或组织之间的厚度可能是前者的指示。
分子生物学
蛋白质结构分析：特别是在分子生物学中，蛋白质的结构是至关重要的知识。当研究蛋白质内的原子如何定位以及蛋白质的折叠和相互作用时，最近点对算法的应用被证明是有用的。
交通与物流
优化路线：在物流和运输中，寻求的解决方案之一是识别最近的仓库或配送点，以最大限度地减少移动距离。这提高了供应链管理的效率并降低了成本。

结论

因此，**最近点对**问题是计算几何中的一个通用问题，在包括空中交通管制和分子生物学在内的多个行业中具有广泛的用途。朴素方法虽然易于实现，但计算量很大；在处理大规模数据时，这种缺点是无法管理的。对于论文中描述的方法，分治法在时间复杂度等于的情况下被认为更有效，使其适用于解决现实生活中快速准确的邻近检测问题。可以注意到，在 C++ 中应用几何学和算法优化的最佳传统可以轻松解决此问题。算法的理解和应用不仅提高了计算速度，而且揭示了解决各种空间问题的基本技术，这就是为什么最近点对问题对于在各个领域进行分析和应用至关重要。

下一个主题C++ 中的 FIFO 推置换算法

← 上一个下一个 →

C++ 最近点对

引言

数学背景

欧几里得距离

暴力破解法

分治法

C++ 实现最近点对的程序

最近点对问题的应用

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

C++ 教程

C++ 控制语句

C++ 函数

C++ 数组

C++ 类和对象

C++ 构造函数

C++ 继承

C++ 多态

C++ 抽象

C++ 命名空间

C++ 模板

C++ 字符串

C++ 指针

信号处理

C++ 异常

C++ 文件与流

C++ STL 教程

面试题

选择题

C++ 程序

C++ STL Stack

C++ STL Bitset

C++ STL Deque

C++ STL List

C++ STL Map

C++ STL Math

C++ STL priority_queue

C++ STL Queue

C++ STL Multiset

C++ STL Multimap

C++ STL Set

C++ STD Strings

C++ STL Vector

C++ 操纵符

C++ STL Algorithms

C++ Algorithm

C++ Iterators

C++ 杂项

C++ 最近点对

引言

数学背景

欧几里得距离

暴力破解法

分治法

C++ 实现最近点对的程序

最近点对问题的应用

结论

相关帖子

C++ 中的计数-最小草图

C++ std::uniform_real_distribution min() 方法

C++ Gomory-Hu 树构造

如何在 C++ 中的 Lambda 函数中捕获 std::vector

C++ 指数搜索算法

C++ 中通过连接非互质节点形成的图的最大连通分量大小

C++ 中的融合树

C++ 零法则

C++ 中 Queue 和 Deque 的区别

C++ 中的莫里斯遍历进行前序遍历

订阅 Tpoint Tech

联系信息