C++ 中的矩阵乘法

在 C++ 编程中，矩阵乘法是基本的线性代数运算，用于计算机图形学、数据科学、工程和物理等多个领域。在 C++ 中，我们可以使用数组和向量实现矩阵乘法。嵌套循环通常用于矩阵乘法，以确定第一个矩阵的行和第二个矩阵的列的点积。

让我们取两个矩阵

• 矩阵 A 的大小： m x n
• 矩阵 B 的维度： n x p

C = A × B 的维度将是 m x p。C[i][j] 的每个分量都按如下方式计算

让我们尝试通过下图理解 3*3 和 3*3 矩阵的乘法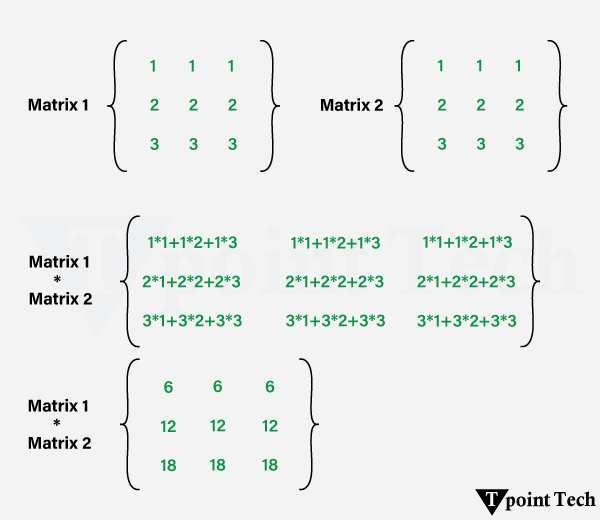

矩阵乘法的条件

在C++ 编程语言中，如果我们想执行矩阵乘法，第一个矩阵 (A) 的列数应该等于第二个矩阵 (B) 的行数。

矩阵乘法规则

C++ 中矩阵乘法有几个规则。其中一些如下：

• 首先，我们必须为矩阵 A 的行创建一个循环。
• 接下来，我们必须为矩阵 B 的列创建一个循环。
• 之后，将相应的元素相乘并求和以计算 C[i][j]。

C++ 中的矩阵乘法示例

让我们举一个例子来说明 C++ 中的矩阵乘法。

输出

Enter the number of row = 3
Enter the number of column = 3
Enter the first matrix element =
1 2 3
1 2 3
1 2 3
Enter the second matrix element =
1 1 1
2 1 2
3 2 1
Multiply of the matrix =
14 9 8
14 9 8
14 9 8

说明

在这个示例中，我们对两个大小为 r × c（用户定义）的方阵执行矩阵乘法。首先，它提示用户为两个矩阵输入一个数字，然后使用三个嵌套循环通过对相应行和列的点积求和来计算乘积。最后，它打印出结果乘法矩阵。

C++ 中的矩阵乘法示例（使用二维数组）

让我们举个例子来演示 C++ 中的矩阵乘法。

输出

Resultant Matrix:
58 64 
139 154

说明

在这个示例中，我们取了两个矩阵 A (2×3) 和 B (3×2) 进行乘法运算，并生成了一个结果矩阵 C (2×2)。之后，我们使用三个嵌套循环来计算 C 的每个元素作为 A 的相应行和 B 的列的点积。最后，它打印出结果矩阵。

结论

总之，矩阵乘法是 C++ 中一个重要的概念。它有助于提高数学理解和编程逻辑。在 C++ 矩阵乘法中，利用嵌套循环有效地计算两个矩阵的行和列的点积，以得到最终的乘积矩阵。

在 C++ 中，在此过程中应密切检查矩阵维度。无论是使用固定大小的数组还是动态输入，它对于数据分析、图形、机器学习和科学计算等多种应用程序都至关重要。

矩阵乘法常见问题

1) 决定矩阵乘法的基本规则是什么？

在 C++ 中，矩阵乘法的主要规则是第一个矩阵的列数应等于第二个矩阵的行数。如果矩阵 A 的大小为 m×n，矩阵 B 的大小为 n×p，则 A×B 的乘法有效，并且结果矩阵的维度将为 m × p。

2) 在 C++ 中执行矩阵乘法需要多少个循环？

在 C++ 中，矩阵乘法中通常使用三个嵌套循环。

• 外层循环遍历初始矩阵的行。
• 中间循环遍历第二个矩阵的列。
• 内层循环在遍历公共维度时计算点积。

3) 是否可以使用向量而不是数组在 C++ 中进行矩阵乘法？

是的，std::vector 可用于管理动态内存。向量比原始数组更安全、更容易使用，并且它们提供了更大的矩阵大小灵活性，特别是对于大型或用户定义的矩阵。

4) 在 C 中，当两个不同维度的矩阵相乘时，会有什么影响？

是的，当两个不兼容维度的矩阵在 C 中相乘时，会有影响。矩阵 A 的维度应与矩阵 B 匹配。如果不满足此条件，则乘法在数学上无效。但是，编译器不会自动检查矩阵维度，特别是当我们使用数组时。

5) 是否有任何 C++ 库可用于处理矩阵？

是的，有几个用于处理矩阵的库，例如 Eigen、Armadillo、Blaze 和 OpenCV。这些库提供集成的维度检查、效率改进和优化的矩阵运算，包括乘法。