C++ 中查找最终安全状态

2025年3月24日 | 7分钟阅读

引言

在计算机科学与图论相关的分支中，有相当多的情况需要找到一些可以定义为“安全”状态/节点的特定状态/节点。如果一个状态开始时系统不会进入任何循环，则该状态被认为是安全的。这类问题在增强系统可靠性、避免死锁和管理依赖性方面具有实际应用。

在本文中，我们将尝试使用 C++ 专注于查找有向图的最终安全状态的问题。我们将详细介绍问题陈述、方法和代码解释。

问题陈述

您有一个有向图，它使用邻接列表表示，并且您可以从一个节点迁移到任何其他节点。为了使一个节点被称为最终安全，离开该节点的所有路径都必须最终到达一个终端节点。终端节点可以定义为没有出边（即不可能迁移到另一个节点）的节点。

目标是识别那些即使从长远来看也是安全的节点。这些是我们需要关注的节点。在这种情况下，许多节点被连续地遵循循环，最终不形成循环（即安全状态）。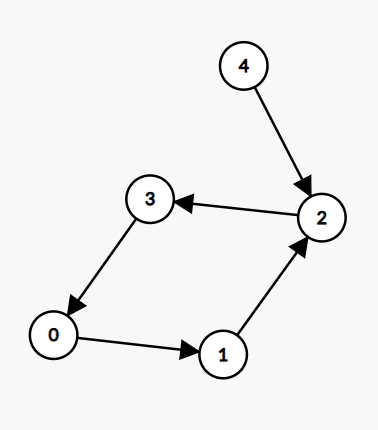

在这个图中

在此情况下，节点 0 被认为是不安全的，因为可以延长和重复此过程。
节点 1、2 和 3 最终也不安全。
节点 4 是最终安全的，因为它的唯一出边指向节点 2 (4 → 2)，并且节点 4 不参与任何循环。

方法

为了解决这个问题，可以对图进行反向，并使用队列实现拓扑排序（如 Kahn 的拓扑排序方法）。我们从终端节点（存在不离开节点的边）的简单情况开始，并逐渐将此方法推广到尽可能多的节点，这些节点的迁移最终将导向安全节点。

步骤：

反转图： 更改图中所有边的方向。这将有助于我们首先处理终端节点。
拓扑排序： 使用队列，并反向处理出列的终端节点。每个被标记为安全的节点将依次支持连续的节点，所有这些节点最终都会变得安全。
返回安全节点： 最后，在所有处理完成后，返回安全节点。

程序 1

#include <iostream>
#include <vector>
#include <queue>
#include<bits/stdc++.h>
using namespace std;

vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
    int n = graph.size();
    vector<vector<int>> reverseGraph(n);   // Reverse graph
    vector<int> outDegree(n, 0);           // Track out-degree of each node
    queue<int> safeQueue;                  // Queue for processing safe nodes
    vector<int> safeNodes;                 // Store eventual safe nodes

    // Reverse the graph and calculate out-degrees
    for (int u = 0; u < n; ++u) {
        for (int v : graph[u]) {
            reverseGraph[v].push_back(u);  // Reverse the edge direction
        }
        outDegree[u] = graph[u].size();    // Original out-degree of node u
    }

    // Nodes with out-degree 0 are terminal nodes and thus safe
    for (int i = 0; i < n; ++i) {
        if (outDegree[i] == 0) {
            safeQueue.push(i);  // Add terminal nodes to the queue
        }
    }

    // Process nodes in the queue
    while (!safeQueue.empty()) {
        int safeNode = safeQueue.front();
        safeQueue.pop();
        safeNodes.push_back(safeNode);

        // For each node that points to the current safe node in reverseGraph
        for (int u : reverseGraph[safeNode]) {
            outDegree[u]--;   // Reduce the out-degree
            if (outDegree[u] == 0) {
                safeQueue.push(u);  // If out-degree becomes zero, it's safe
            }
        }
    }

    // Sort the eventual safe nodes for output
    sort(safeNodes.begin(), safeNodes.end());

    return safeNodes;
}

int main() {
    vector<vector<int>> graph = {{1, 2}, {2, 3}, {5}, {0}, {5}, {}, {}};
    
    vector<int> safeNodes = eventualSafeNodes(graph);

    cout << "Safe nodes are: ";
    for (int node : safeNodes) {
        cout << node << " ";
    }
    cout << endl;

    return 0;
}   

输出

 
Safe nodes are: 2 4 5 6

代码解释

反转图： 为了确定最终能回溯到终端节点的节点，将首先发现终端节点及其依赖项的松弛，然后发现与之连接的节点。在反转图中，原始边 u → v 转换为 v → u。
计算出度： 对于每个节点，计算从该节点出发的边数（出度）。一些新添加的最终节点是没有出度的节点，并将被放入 safeQueue。
管理安全节点
- 对于 safeQueue 中的每个节点，我们减少在图的反方向上指向它的节点的出度。
- 如果任何节点的出度变为零，则表示它的所有后续节点最终都是安全的，并且该节点将被放入待处理队列。
输出： 最后，安全节点被写入并打印。

时间复杂度

图反转： O(E)，E 是边的数量。
拓扑排序： O(V + E)，V 是顶点的数量，即节点，E 是边的数量。

因此，总时间复杂度为 O(V + E)，这对于大多数实际图来说是合理的。

空间复杂度

图存储： /in 和 /out 图（对于两个图）被认为是简化的 O(V+E) 和 O(E + V) 分别。
出度数组： O(V)
队列和结果阶段： O(V)

因此，总空间复杂度为 O(V + E)。这种空间和时间复杂度非常令人满意，并且符合图平面化在实践中的应用目标，而这正是大多数图算法应用的地方。

程序 2

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <unordered_map>

using namespace std;

class Graph {
public:
    Graph(int n) : adjList(n), reverseGraph(n), outDegree(n, 0) {}

    void addEdge(int u, int v) {
        adjList[u].push_back(v);
        reverseGraph[v].push_back(u);
        outDegree[u]++;
    }

    vector<int> eventualSafeNodes() {
        int n = adjList.size();
        queue<int> safeQueue;
        vector<int> safeNodes;

        // Identify terminal nodes (out-degree 0)
        for (int i = 0; i < n; ++i) {
            if (outDegree[i] == 0) {
                safeQueue.push(i);
            }
        }

        // Process nodes in the queue
        while (!safeQueue.empty()) {
            int safeNode = safeQueue.front();
            safeQueue.pop();
            safeNodes.push_back(safeNode);

            // Process the reverse edges
            for (int u : reverseGraph[safeNode]) {
                outDegree[u]--;   // Decrement out-degree
                if (outDegree[u] == 0) {
                    safeQueue.push(u);  // If out-degree becomes zero, it's safe
                }
            }
        }

        // Sort the eventual safe nodes for output
        sort(safeNodes.begin(), safeNodes.end());
        return safeNodes;
    }

private:
    vector<vector<int>> adjList;      // Adjacency list for the original graph
    vector<vector<int>> reverseGraph; // Adjacency list for the reversed graph
    vector<int> outDegree;             // Out-degree of each node
};

int main() {
    // Create a directed graph with 8 nodes
    Graph g(8);
    
    // Add edges to the graph (example)
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(1, 3);
    g.addEdge(2, 4);
    g.addEdge(3, 0);
    g.addEdge(3, 5);
    g.addEdge(4, 5);
    g.addEdge(5, 6);
    g.addEdge(6, 7);

    vector<int> safeNodes = g.eventualSafeNodes();

    cout << "Safe nodes are: ";
    for (int node : safeNodes) {
        cout << node << " ";
    }
    cout << endl;

    return 0;
}   

输出

 
Safe nodes are: 2 4, 5 6, 7

说明

图类： 包含我们图特征的 Graph 类在此进行了阐述。它包含
邻接表： 图的邻接列表，包含原始图的 vector 组成的 vector。
reverseGraph： 图的反向 vector 组成的 vector。
outDegree： 用于存储节点出度的 vector。
添加边： addEdge 函数用于绘制从节点 u 到节点 v 的箭头。此操作同时作用于邻接列表和反转图，并且还将更新节点 u 的出度。

查找最终安全节点

提供了一个队列，其中包含所有没有出边（出度为 0）的节点。
在上一节中，我们也强调了如何确定终端节点并将其添加到队列中。
当队列中的每个节点被处理时，指向它们的（在反转图中）具有指向当前节点的边的其他节点的出度将减一。如果任何此类节点的出度变为零，则该节点也将被添加到待处理队列中。
排序和输出： 最后，在完成排序后，将安全节点返回，以便以有序的方式返回。

时间复杂度

时间复杂度被认为是整体 O(V+E)，其中 V 是顶点（节点），E 是边。构建反转图的成本为 O(E)。处理队列也需要 O(E+V)，因为每个顶点和边都被访问一次。

空间复杂度： 空间复杂度为 O(V+E)

优点

死锁预防： 在操作系统中，资源的分配也可以以消除死锁条件的方式进行。所谓的安全状态有助于设计资源分配策略。
依赖管理： 项目或软件开发中的任务管理通常涉及相互依赖的任务。安全状态可以指导任务的调度方式，以确保所有依赖项都已清除。
电路设计： 在电子电路中，当提供相应输入时，需要产生输出，而不会产生任何不希望有的振荡或扩展和结束的反馈。安全状态可用于电路分析和稳定电路设计。
博弈论： 理解游戏中的安全状态很重要，因为玩家可以通过它们知道哪些走法可以保证他们获胜或避免失败，尤其是在轮流进行走法的游戏中。
数据流分析： 编译器使用数据流分析，其中数据流经不同组件，以确定不会发生数据竞争或不一致的其他状态，从而不会发生程序通信错误。
网络路由： 在通信网络中，数据包路由到其他进程的方式需要避免形成环路，这可以提高系统传递数据的可靠性和效率。

结论

总之，这篇 C++ 文章侧重于如何确定有向图的最终安全属性。反转图和计算拓扑顺序有助于算法上解决这个问题。理解这个概念在需要避免死锁、进行依赖管理或实现系统可靠性的情况下至关重要。

下一主题C++ 中的 dlsym() 函数

← 上一个下一个 →

C++ 中查找最终安全状态

引言

问题陈述

方法

步骤：

程序 1

代码解释

程序 2

说明

优点

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

C++ 教程

C++ 控制语句

C++ 函数

C++ 数组

C++ 类和对象

C++ 构造函数

C++ 继承

C++ 多态

C++ 抽象

C++ 命名空间

C++ 模板

C++ 字符串

C++ 指针

信号处理

C++ 异常

C++ 文件与流

C++ STL 教程

面试题

选择题

C++ 程序

C++ STL Stack

C++ STL Bitset

C++ STL Deque

C++ STL List

C++ STL Map

C++ STL Math

C++ STL priority_queue

C++ STL Queue

C++ STL Multiset

C++ STL Multimap

C++ STL Set

C++ STD Strings

C++ STL Vector

C++ 操纵符

C++ STL Algorithms

C++ Algorithm

C++ Iterators

C++ 杂项

C++ 中查找最终安全状态

引言

问题陈述

方法

步骤：

程序 1

代码解释

程序 2

说明

优点

结论

相关帖子

C++ std::views::drop

C++ 集合覆盖问题

C++ 中的最优文件合并模式

C++ 串排序算法

C++ rewinddir() 函数

C++ 中的西尔维斯特序列

C++ 中分段筛（打印范围内的素数）

C++ 区域分配

C++ Tutte 定理

C++ std::countr_zero