C++ 中的恩特林格数

在本文中，我们将讨论 C++ 中的 Entringer 数及其多种实现方法。

什么是 Entringer 数？

Entringer 数用 E(n, k) 表示，其中 n 是元素总数 +1，k 表示元素中应存在的上升数。Entringer 数将提供可能的排列数，其中数字是递增和递减的，并且该排列必须包含 k 个上升。

例如

如果 Entringer 数是 E(4, 2)，则可能的排列数为

3 2 4 1 5

3 2 5 1 4

3 1 4 2 5

3 1 5 2 4

因此，可能的总排列数为 4

Entringer 数的应用是

这些数字主要用于组合枚举。这些 Entringer 数使用动态规划计算，并用于算法实现。这些数字提供了组合关系和结构。

示例 1

让我们编写一个 C++ 程序来计算 Entringer 数。

输出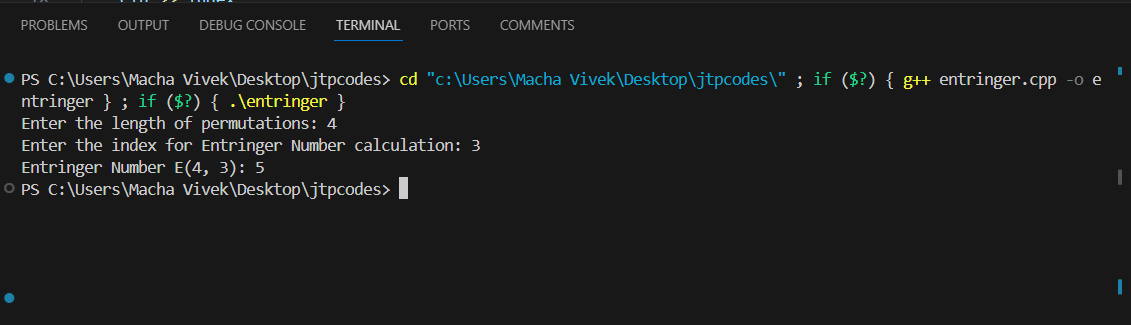

说明

程序中存在的变量是 length，它表示排列的长度，以及 index，它表示 Entringer 数表示中的 k 值。这些值作为输入从用户处获取。“entringerNumber”是一个使用递归计算 Entringer 数的函数。

递归函数以 number 和 index 作为参数。当 length 等于零且 index 等于零时，我们都知道只有一个可能的 Entringer 数，因此它返回 1。如果 index 为零且 length 不等于零，它将返回零。否则，将有两个递归调用：一个将 length 减 1，另一个将 length 和 index 都减 1。在主函数中，首先调用这个 entringerNumber。

示例 2：使用动态规划

让我们编写另一个 C++ 程序来使用动态规划计算 Entringer 数。

输出

说明

该程序在给定 length 和 index 时计算 Entringer 数。该程序优化了上述递归方法。该程序使用动态规划来减少运行时。在此程序中，用户必须输入 length 和 index。使用大小为 length+1 和 index+1 的 2D 向量。之后，使用嵌套循环遍历 DP 表的单元格，从 (1,1) 到 (length, index)。在这里，使用公式 E(i,j) = E(i,j-1) + E(i-1,j-1) 来计算 Entringer 数。计算出的值存储在 DP 表中，并可在后续迭代中使用。

示例 3：使用动态规划和优化空间

让我们编写一个 C++ 程序来使用动态规划和优化空间来计算 Entringer 数。

输出

说明

这个程序是对上一个程序的空间优化。在之前的程序中，使用 2D 数组进行动态规划，但这里使用单个数组进行动态规划，因此该程序所需的空间将是 O(n)，运行时为 O(n*k)。