Arima Garch 模型

时间序列分析是一个涉及理解数据中模式性质以对未来趋势做出适当预测的过程。在众多可用模型中，ARIMA-GARCH 因其能够处理具有非常复杂结构的数据（包括趋势、季节性和波动率聚集）而脱颖而出。这种混合模型结合了两个强大的统计工具：ARIMA 模型，用于捕捉数据的均值和趋势；GARCH 模型，用于捕捉波动率或时变方差。这两种模型的集成使得 ARIMA-GARCH 特别适用于以趋势和波动率波动时期为特征的金融和经济数据集。

就时间序列的线性而言，ARIMA 通过结合三个主要部分来捕捉这一点：自回归，衡量过去值与其当前值观测值的关系；差分，旨在通过稳定序列来使其均值平稳；以及移动平均，用于对不同类型观测值之间的依赖关系以及预测误差进行建模。该部分标记为 ARIMA(p, d, q)，其中 p 表示自回归使用的参数数量，d 表示差分阶数，q 表示移动平均参数。GARCH 部分代表 ARIMA 无法捕捉的残差变化的方差。它捕捉了金融时间序列中经常出现的波动率聚集现象，即高波动率时期往往紧随更多高波动率，低波动率时期紧随低波动率。所有这些共同帮助 ARIMA-GARCH 模型处理时间序列数据中的复杂模式。

当数据时间序列同时表现出趋势或季节性以及随时间变化的方差时，ARIMA-GARCH 模型非常有效。例如，在金融市场中，股票价格通常有趋势，但也有需要建模的波动时期，以便正确评估风险。ARIMA 部分处理趋势，而 GARCH 组件处理波动率，但模型调整以考虑这两个方面。同样，在宏观经济预测中，GDP 增长或通货膨胀率等数据通常需要一个能够考虑潜在趋势并适应经济不确定性加剧时期的模型。

ARIMA GARCH 模型的工作原理

对于 ARIMA-GARCH 模型，探索性数据分析将从绘制时间序列图以查找模式开始，然后使用平稳性检验，例如增广迪基-富勒 (ADF) 检验。接下来，拟合 ARIMA 模型到数据以捕捉均值结构，并检查其残差是否存在异方差性，例如方差递增的序列。如果存在此类模式，则将 GARCH 模型拟合到残差中以捕捉和预测波动率。最后将这两个模型集成，从而提供一个更全面的预测框架。

股票价格作为典型的金融时间序列，通常会经历不可预测的涨跌，导致剧烈的波动，称为波动率聚集。本质上，高波动率时期往往紧随更多高波动率，平静时期则紧随平静时期。这种行为使得预测这些时间序列变得特别具有挑战性。现在，借助 ARIMA-GARCH 模型，我们将解决这个问题。

导入库

我们将设置参数并提取数据。

输出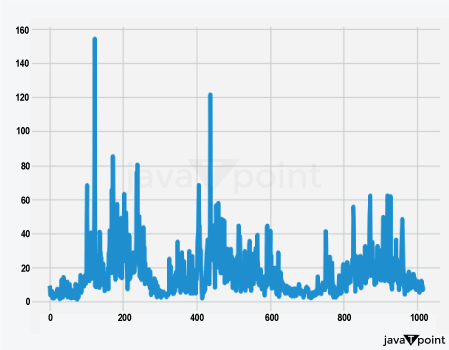

输出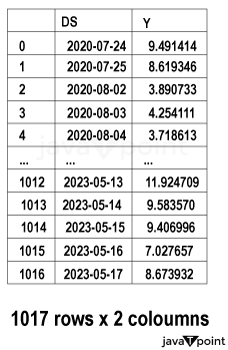

让我们检查平稳性。

输出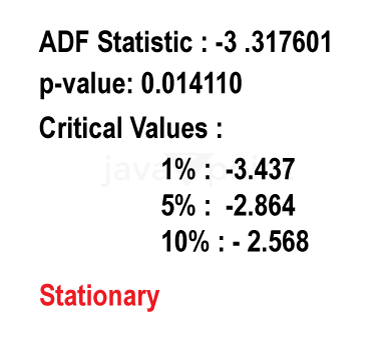

输出

以下是您的 ARIMA 模型。

输出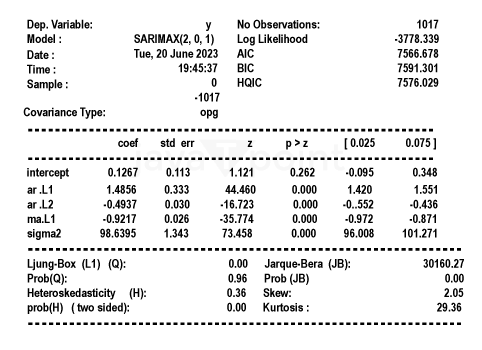

输出

 
Optimal parameters are [2, 0, 1]

# Best model from AutoARIMA
fig = auto_best_model.plot_diagnostics(figsize=(12,10))
plt.show()   

输出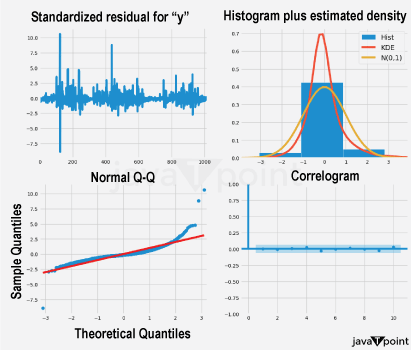

输出

异方差性

将理想化的时间序列视为一系列独立同分布的观测值。理解这个序列。从分布中估计参数足以理解它。这就是平稳性的概念。一旦有了分布，就可以通过数据学习其参数并进行预测；至少它从不会比这更难。这本质上是关于一些具有条件异方差性的时间序列以及我们用来预测它们的模型的内核。

如果我们回到理想化的时间序列，异方差性是指用于构建我们时间序列的潜在分布的方差随时间变化。异方差性的典型表现是时间序列的方差随时间增加，以圆锥形模式向外扩展。有时，如果异方差性仅存在少量，则可能会被掩盖，并且可以通过使用 Box-Cox 变换将数据分布移向某种正态来进一步减小。然而，在我们对 S&P500 的预测中，我们方差的变化太大而没有被掩盖，而是在方差的 xt 条件下，所有前一个时间步的方差：xt-1。因此，这被称为条件异方差性或波动率聚集。

波动率聚集

时间序列锯齿状峰值背后的根本行为是波动率聚集。观察上面的图，我们可以看到存在高波动率和低波动率时期。存在形成正反馈循环的时期，方差的变化导致方差的更大变化，并被相对平静的时期打断。我们稍后讨论的 ARCH 和 GARCH 模型用于时间序列具有变化方差的情况。实际上，这些模型不生成估计值。然而，ARCH 和 GARCH 模型捕捉模型中残差的预期方差。再次，对于建模真实数据，我们应用 ARIMA 然后 ARCH 或 GARCH。

自回归条件异方差性

在 AR 模型中，当前时间步的值是 p 个滞后值的函数，其中 p 个值与当前时间步高度相关。在 ARCH 方差中，当前时间步是滞后 p 个标准误差平方的函数，由参数 α 给出。标准误差就是观测值与通过另一个模型获得的预测值之间的差值。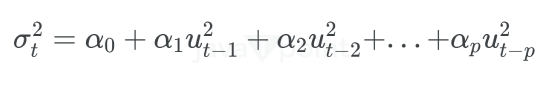

如果波动率倾向于聚集，那么最近的大平方误差很可能导致大的方差和更多的大平方误差。就像拟合 AR 模型一样，我们可以查看 PACF 和 ACF 图来查看我们的序列在何处自相关，并使用它来选择参数 p 的值。如果我们有一个 ARCH(1) 或一阶 ARCH 模型，那么除了方差的变化之外，我们假设它是平稳的。很多时候，我们将 AR 或 ARMA 模型与 ARCH 模型结合起来，通过获取 ARMA 模型的平方残差并将其输入 ARCH 模型。我们还可以将均值过程输入 ARCH。在这种情况下，在 内核中，我们输入股票收盘价变化的百分比——这将是一个围绕 0 波动的时间序列。

广义自回归条件异方差性

GARCH 扩展了 ARCH，使其方差能够依赖于自身的滞后以及平方残差的滞后。GARCH 捕捉更高变化，例如上升和下降的波动率。

GARCH(q, p) 有两个参数。

q: 滞后方差数

p: 滞后残差误差数

这里使用的参数遵循 ARCH Python 库，但大多数时候我们使用交换的符号。

如果异方差性和波动率聚集是该过程的关键特征，GARCH 通常比 ARCH 更能模拟数据；我们将进行 GARCH 和 ARCH 的拟合并描述拟合差异，但是纯 GARCH 模型有大量的扩展，引入了许多新参数来处理波动率可以采取的特定形式。

这是我们 GARCH(2,1) 模型的结果

Omega 是模型的方差。因此，收益的标准差是 omega 的平方根，这里是 60%。这意味着我们的收益可以为 0，标准差为 60，这使其非常不稳定。模型中的这种自相关会抑制波动率的激增和低波动率日期的聚集，而我们的模型非常擅长产生非常大的激增。现在是我们的 alpha 和 beta 系数。Alpha 衡量波动率数据（例如今天的）有多少会被馈送到下一期的波动率中。在我们的模型中，9% 的上一期波动率将传递到第二天。Beta 是我们的持久性参数，如果 beta 大于 1，则会导致小冲击的正反馈循环，从而产生失控的波动率。

这是我们波动率的衰减率。如果 alpha 加 beta 等于 1，那么我们就处于我们模型中的持久性波动率情况，我们可能会寻找其他选项，例如 IGARCH。

Alpha 的范围通常是 0.05<α<0.1，参数 beta 是 0.85<β<0.98。这些范围不完全适用于预测数据，但可以让我们了解我们应该看到的值。现在我们有了 t 统计量和 p 值。T 是我们的估计值除以标准误差，用于计算我们的 p 值。通常的零假设是我们的系数没有影响，但如果我们的 p 值小于 alpha (0.05)，我们可以拒绝零假设。一旦我们开始使用更多参数的模型，就需要关注 p 值。上面我们进行了一些拟合优度检验，我们将在稍后介绍。所有检验都告知我们应该拒绝零假设，因此我们继续寻找更好的模型参数。

现在我们将使用 Ljung Box 检验、Engle's Arch 和 Shapiro Wilk 检验来检查我们模型的拟合情况。

输出

输出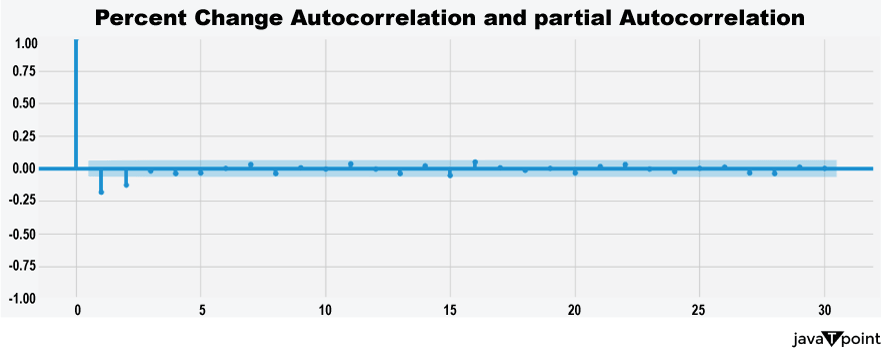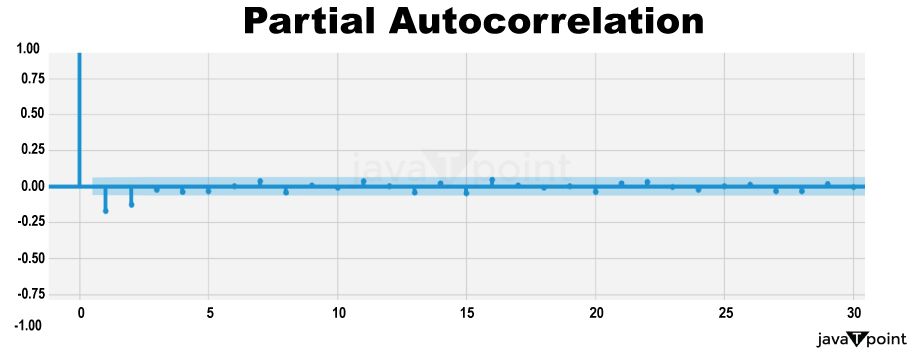

输出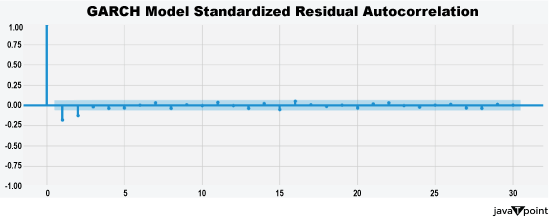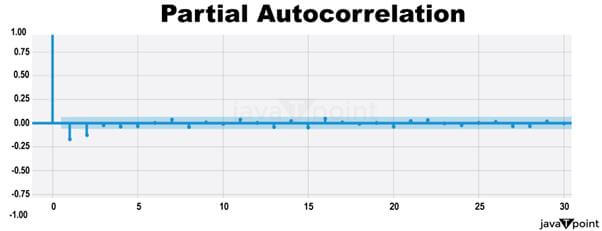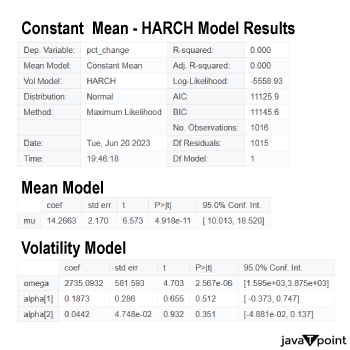

输出

输出

 
Time series is heteroskedasticity   

Garch 分析

我们将使用网格搜索机制，根据赤池信息准则 (AIC) 和残差诊断测试来确定最佳 GARCH 模型。

各种 Garch 模型

现在我们将使用 GARCH 系列模型来评估时间序列的波动率。

输出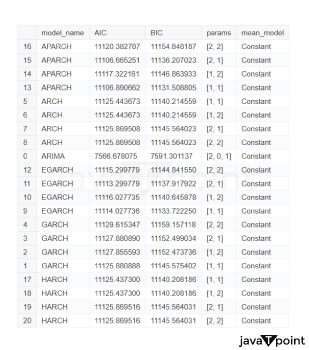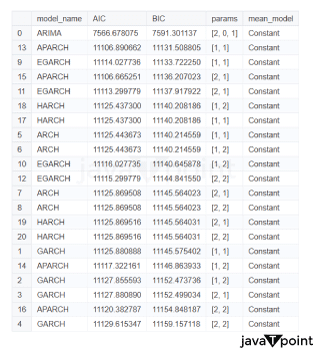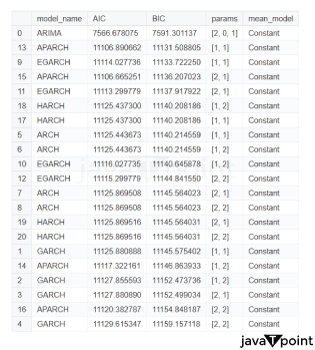

在这个模型集合中，ARIMA 参数为 ([2, 0, 1]) 的模型是明显的赢家，其 AIC 为 7566.68，BIC 为 7591.30，显著优于所有其他模型。由于其优越的拟合度，它最适合该数据集。在波动率模型中，APARCH[2, 1] 报告了最低的 AIC 11106.67 和 BIC 11136.21，因此是建模异方差性的最佳选择。APARCH 的其他规格：[1, 1] 和 [1, 2] 的表现相对较好，但不如 APARCH [2, 1]。ARCH 和 GARCH 的性能非常接近。性能最佳的模型版本是 ARCH [1, 1] 和 GARCH [1, 1]，AIC = 11125.44，BIC = 11140.21。然而，这些模型在波动率动态方面的表现不如 APARCH 和 EGARCH 模型。