机器学习中的生存分析

生存分析是一种用于分析时间-事件数据的统计方法。它涉及研究事件发生所需的时间，例如患者疾病进展或死亡的时间。机器学习可用于生存分析，以模拟事件和预测变量之间的关系。

一种流行的使用机器学习进行生存分析的方法是Cox比例风险模型。该模型允许估计风险函数，该函数代表在任何给定时间基于预测变量发生事件的瞬时概率。Cox比例风险模型假设风险函数在预测变量的不同水平上是成比例的。

另一种使用机器学习进行生存分析的方法是随机生存森林 (RSF) 模型。RSF 模型是随机森林算法的扩展，专门为生存分析而设计。RSF 模型使用决策树根据预测变量将数据分割成子组，并估计每个子组的生存概率。

还有基于深度学习的生存分析方法，例如DeepSurv 模型，它使用神经网络来估计风险函数。DeepSurv 旨在处理具有高维预测变量的大型数据集，并能捕获预测变量与事件之间的复杂关系。

基于机器学习的生存分析可用于多种应用，例如预测患者预后、估计设备发生故障所需的时间或模拟物种在生态系统中的生存情况。需要注意的是，这些模型需要仔细的验证和解释，因为生存分析可能会受到删失数据和其他偏差的影响。

为了更好地理解，我们将尝试分析乳腺癌（METABRIC）数据集。

代码实现

• 导入库

• 时间-事件数据

每个主题都有一个时间周期和一个事件在时间-事件数据中。测量发生事件所需的时间。这个时间段可能是患者癌症诊断或治疗开始与其死亡之间的时间跨度，也可能是肿瘤扩散或局部复发之间的时间跨度。事件不一定是负面的。恢复或任何其他积极的事情都可以包括在内。时间-事件数据有时也称为生存时间或失效时间数据，这源于最初研究的时间-事件数据实例。为解决这些问题而开发的统计方法被称为生存分析。

本文中的分析使用了乳腺癌（METABRIC）数据集。它包含 2509 名乳腺癌患者的临床特征以及诊断与复发和死亡之间间隔的信息。

• 加载数据集

输出

• EDA

如前所述，METABRIC 数据集包含 2509 名不同的乳腺癌患者。这些患者的平均诊断年龄介于 21.9 至 96.3 之间，平均为 60.4 岁。患者接受了乳房切除术（切除乳房的所有乳腺组织）或保乳手术（切除癌症所在的乳房部分）。虽然乳腺肉瘤是一种极其罕见的乳腺癌，占所有乳腺癌的不到 1%，但数据集中有 2506 名乳腺癌患者和 3 名乳腺肉瘤患者。浸润性导管癌 (IDC) 是最常见的组织学亚型，占乳腺癌病例的 1865 例。IDC 占所有乳腺癌诊断的 80%，使其成为最常见的类型。这些迹象表明该数据集有效地捕捉了真实世界的情况。

输出

数据集中报告了两个事件。结果是无复发自由状态（Relapse Free Status）和总生存状态（Overall Survival Status）。此外，这些事件有两个持续时间：总生存期（月）和无复发生存期（月）。这两个事件及其持续时间是生存分析的基础。虽然两种持续时间的分布非常相似，但事件的分布略有不同。在生存事件中，“已死亡”标签更频繁，表明事件已发生，而在复发事件中，“未复发”标签表明事件未发生。

输出

患者的临床特征是数据集中的附加特征。这些特征包括肿瘤的细胞数量、患者是否接受过化疗、激素治疗、放疗，患者的 ER、PR 和 HER2 状态，以及肿瘤的大小、分期和组织学亚型。虽然包含这些特征作为生存分析模型的变量需要额外的预处理和清理，但这是可行的。

输出

• 预处理和清理

只有五个列没有缺失值，而 29 个列有缺失值。性别、癌症类型详情、癌症类型、Oncotree 代码和患者 ID 是这些列。其他列不提供任何信息；然而，癌症类型和癌症类型详细信息可以非常有助于估算。

输出

在估算阶段，利用了不同列之间的依赖关系。持续时间列中的缺失值用癌症类型详细事件组的最常见值填充，而事件列中的缺失值用其最常见值填充。ER、PR 和 HER2 状态列的空白用其测量技术列的最常见值填充（ER 状态通过 IHC 测量，HER2 状态通过 SNP6 测量）。化疗、激素治疗和放疗的缺失值用癌症类型详细类别中最常见的值填充。根据它们之间的相互依赖性，使用各种组的众数或中位数来填充其他列中的缺失值。对于一些无法一次性完成的列，使用了迭代填充。最后，移除了患者的生命状态字段，因为它不再为研究提供额外数据。

在预处理过程结束时，将对象类型列进行标签编码并转换为 uint8 以节省内存。由于 LabelEncoder 可能将“事件发生”编码为 0，因此对两个事件列——总生存状态和无复发生存状态——进行手动编码。这完成了笔记本的介绍部分，并为模型准备了数据。

现在每一列都是一个数字，可以确定它们的关联性。由于许多属性相互依赖，存在一些大于 0.6 和小于 -0.6 的显着相关性。细胞数量和整合簇之间存在一个完美的正相关，因此应删除其中一个。一个关键因素是需要考虑总生存状态对无复发生存状态的依赖性。因此，不应使用此类特征作为协变量。Sex 列对应于最后一行和最后一列。鉴于所有患者都是女性，Sex 列没有方差，也没有关联。因此，两者都为空。

输出

理论

生存函数

与生存分析相关的技术组的目的是使用生存数据计算生存函数。设 T 为从研究数据集中提取的（可能无限，但始终为正）随机时间。S(t)，即群体的生存函数，由公式 S(t)=Pr(T>t) 给出。事件尚未在时间 t 发生的可能性，或者更准确地说，生存超过时间 t 的概率，由生存函数简单定义。

随机寿命 T，不能为负，是从待研究数据集中提取的。生存函数 S(t) 是 t 的非递增函数，其值在 0 和 1 之间。在时间段的开始（t=0）时，还没有受试者遇到事件。因此，生存超过时间零的概率 S(0) 为 1。由于如果研究时间段是无限的，每个人最终都会遇到感兴趣的事件，因此 S(∞)=0，因为生存的概率最终会达到零。虽然原则上生存函数是平滑的，但实际上事件是在特定时间段内观察到的，例如天、周、月等，使得生存函数的图形类似于阶跃函数。

风险函数

给定事件尚未发生的情况下，风险函数 h(t) 提供了事件在时间 t 发生的可能性。它描述了每单位时间事件可能发生的瞬时概率。它表示为

??(?≤?≤?+??|?>?)

此量除以间隔 t，因为当 t 减小时它变为零。时间 t 的风险函数 h(t) 定义为

因此，风险函数模型显示了哪些时间段发生事件的可能性最大或最小。风险函数不必像生存函数那样从 1 开始并减小到 0。通常，风险率随时间波动。它可以从任何值开始，并随时间波动。

删失

理解删失是生存分析的一个基本要素。生存分析中有两种类型的观察值

• 事件已发生，并且可以在发生时测量。
• 在该时间段内未观察到事件，并且只知道未观察到事件的总天数（删失）

存在两组，一组是事件发生的时间被精确知道，另一组是不知道。对于第二组，感兴趣的事件在特定时间段内未发生。这些个体是删失的。不考虑删失组是一个常见的错误。尽管不知道如果我们在更长的时间内观察该个体，事件是否会发生，但事实是事件未发生，表明该事件不太可能发生在该个体身上。

我们无法无限期地跟踪一个人，这是删失的一个原因。研究必须在某个时间结束，并非所有人都会经历事件。另一个常见因素是研究参与者失访。我们称之为随机删失。当由于研究者无法控制的原因而中止随访时，就会发生这种情况。

在生存分析中，删失观测值会一直增加到不再被跟踪为止的总风险人数。这种方法的一个好处是，并非每个人都需要被跟踪相同的时间。该分析可以考虑到每个观测值的随访时间可能不同。

右删失、左删失和区间删失是三种不同的删失形式。

右删失

右删失是最常见的删失类型。当随访期右侧的生存时间不完整时，就会发生这种情况。考虑一项临床试验（研究结束 - 研究开始）持续一段时间，其中涉及三名患者（A、B 和 C）。下图显示了 3 名患者的不同路径。

• 患者 A：在研究结束前发生了事件。
• 患者 B：活到了研究结束。
• 患者 C：退出了实验。

患者 A 不需要被删失，因为我们确切地知道他们能活多久或他们死亡的时间。然而，由于我们不知道患者确切的生存时间，需要对患者 B 进行删失。只知道他们在研究期间的生存情况。由于患者 C 在研究结束前退出了试验，他们也需要被删失。由于我们不知道患者的实际生存时间，我们只能假设他们活到了退出时。在右删失中，实际生存时间将始终等于或长于观测到的生存时间。

输出

左删失

当我们无法确定事件发生的准确时间时，就会发生左删失。由于显而易见的原因，如果事件是死亡，则数据不能是左删失。病毒检测是一个典型的例子。例如，如果我们一直在监测一个人并注意到病毒检测呈阳性，但我们不确定该人暴露于疾病的确切时间。只知道在该人接触到疾病的时间是在零和检测时间之间。

区间删失

如果，就像病毒检测一样，我们在某个时间点（t1）对该人进行了检测，结果呈阴性，那么情况如下。然而，在稍后的时间点（t2），该人的检测结果呈阳性。在这种情况下，我们知道该人在 t1 和 t2 之间暴露于病毒，但我们不确定暴露的确切时间。这可以作为区间删失的一个很好的例子。

求值

一个优雅的解决方案是，将数据的删失以及生存时间频繁出现的偏态分布，转化为一个排序问题。不仅可以对两个受试者的生存时间进行排序（如果它们都未被删失），也可以对其中一个受试者的未删失持续时间短于另一个受试者的情况进行排序。

一致性指数（CI），也称为 c 指数，是生存模型最常用的性能指标之一，原因如上所述。它可以被理解为所有受试者配对中，估计生存时间被正确排序的比例。换句话说，它是估计生存时间和观测生存率一致的概率。有一种方法可以写成

使用指示函数 1ab=1 如果 ab，否则为 0。模型 f 对受试者 I 的预期生存时间表示为 f(xi)。该指数可与连续输出变量一起使用并考虑数据删失，这使其成为 Wilcoxon-Mann-Whitney 统计量的推广，因此也是 ROC 曲线下面积 (AUC) 到回归问题的推广。C = 1 表示完美的预测准确性，而 C = 0.5 等同于随机预测器，这与 AUC 类似。

一致性指数在 Lifelines 包中实现。它需要 3 个参数：预测得分（类数组的部分风险率或生存时间）、事件时间（具有与数组相似的持续时间的类似对象）和事件已观察（类数组的二进制事件数据）。使用签名 lifelines.utils.concordance_index(event_times, predicted_scores, event_observed)，可以调用评分函数。返回值是模型断言 X 大于 Y 的频率的平均值，而实际上 X 大于 Y 在观测数据中。该函数也处理删失值。

对某些时间点的事件概率进行排名是评估生存模型的另一种方法。下面的 time-dependent roc_auc_score 函数可用于此过程。它首先将形状为 (n_samples, 1) 的真实标签转换为形状为 (n_samples, n_evaluation_times) 的矩阵。之后，在每个时间点（列）计算 sklearn.metrics.roc_auc_score。

生存模型

生存分析模型需要一种特定的数据集格式

• E 是事件指示符，其中 Ei=0 表示删失，Ei=1 表示事件发生。
• T 是观测时间。
• X 是一个 n 维特征向量。（协变量）

估计生存的三种主要传统方法是：非参数、半参数和参数技术。参数方法的前提是生存时间的分布符合特定的概率分布。这些技术包括威布尔、指数和对数正态分布等。这些模型通常使用特定的最大似然估计来预测参数。在使用非参数方法时，不依赖于底层分布的参数形状。非参数技术通常用于呈现个体人群的平均图景，并将生存概率描述为时间的函数。Kaplan-Meier 估计器是最常用的单变量方法。Cox 回归模型基于参数和非参数组件，属于半参数方法。

交叉验证使用具有五个折叠的 StratifiedKFold 进行。Cancer Type Detailed 是分层的。但是，由于某些值的稀有性，一些值没有被正确分层。使用相同的拆分方法使用保留的测试集进行最终评估。

Kaplan-Meier 估计（非参数模型）

Kaplan-Meier 估计是估计生存函数最常用的非参数方法。在删失存在的情况下，非负回归和单个随机变量（初始事件时间）的密度估计是思考生存分析的另一种方式。在删失的情况下，Kaplan-Meier 是一个非参数密度估计（经验生存函数）。该模型的好处是高度灵活，模型复杂度随观测数的增加而增加。然而，有两个缺点

1. 由于难以添加变量，因此难以定义个体生存函数差异如何取决于个人特征。主要方法是拟合多个子群体的模型并进行比较。然而，随着属性数量和这些属性值的增加，这种方法难以扩展。
2. 生存机制效率不高。具体来说，它们是分段常数。随着样本量的增加，它们会更接近平滑估计器，但对于小样本，它们仍然与之相去甚远。死亡概率可能突然增加或减少的假设并不可完全信服。此外，如果在某个时间段内没有死亡观察值，它会将该时间段 [0,t] 的生存概率指定为 1，这可能不是您想要的。存在用于核平滑的技术，可用于改进生存函数。然而，理解结果可能很困难。

Kaplan-Meier 估计器的主要原理是将生存函数 S(t) 的估计分解为基于观测到的事件时间的更易于管理的阶段。使用以下公式计算每个时间段结束时的生存概率

尽管数据被划分为训练集、验证集和测试集，但 Kaplan-Meier Fitter 首先被拟合到整个数据集。这是利用 Kaplan-Meier 估计来获得人口的整体概览的一种方法。对于总生存状态和无复发生存状态事件，估计的 S(t) 显示为人群总体的分步函数。

y 轴显示患者在 t 个月后仍然存活或未复发的可能性，x 轴表示 t 个月。为了描述我们对这些点估计的不确定性，然后由区域填充在直线周围，置信区间是必需的。估算中的不确定性越大，置信区间越宽，反之亦然。置信区间是计算并存储在 fit() 调用下的 confidence_interval_ 属性中。指数 Greenwood 置信区间用于该过程。由于在时间 t 未知其事件时间，点表示相应的删失患者。

可以明显看出，事件未发生的可能性在研究开始时很高，并随时间降至零。由于预测未来更加困难，因此在研究开始时进行的估计更具信心，而在研究结束时进行的预测则不那么有信心。

Kaplan-meier 估计也可用于预测未观测数据随时间生存的可能性。Lifelines.KaplanMeierFitter. predict 函数的 times 参数是应预测概率的时间步长列表。例如，下面的模型旨在预测在 12、24 和 36 个月时这两种事件（单独）的发生。使用 5 折交叉验证和一个未知的测试集来评估模型。

测试 ROC = 0.5 根据 AUC 结果，Kaplan-Meier 估计无法推广到新的测试集。考虑到我们的模型不包含患者特征，并且为社区中的每个患者生成相同的概率，这是可以预期的。因此，Kaplan-Meier 估计最适合用于探索性数据分析，而不是进行预测。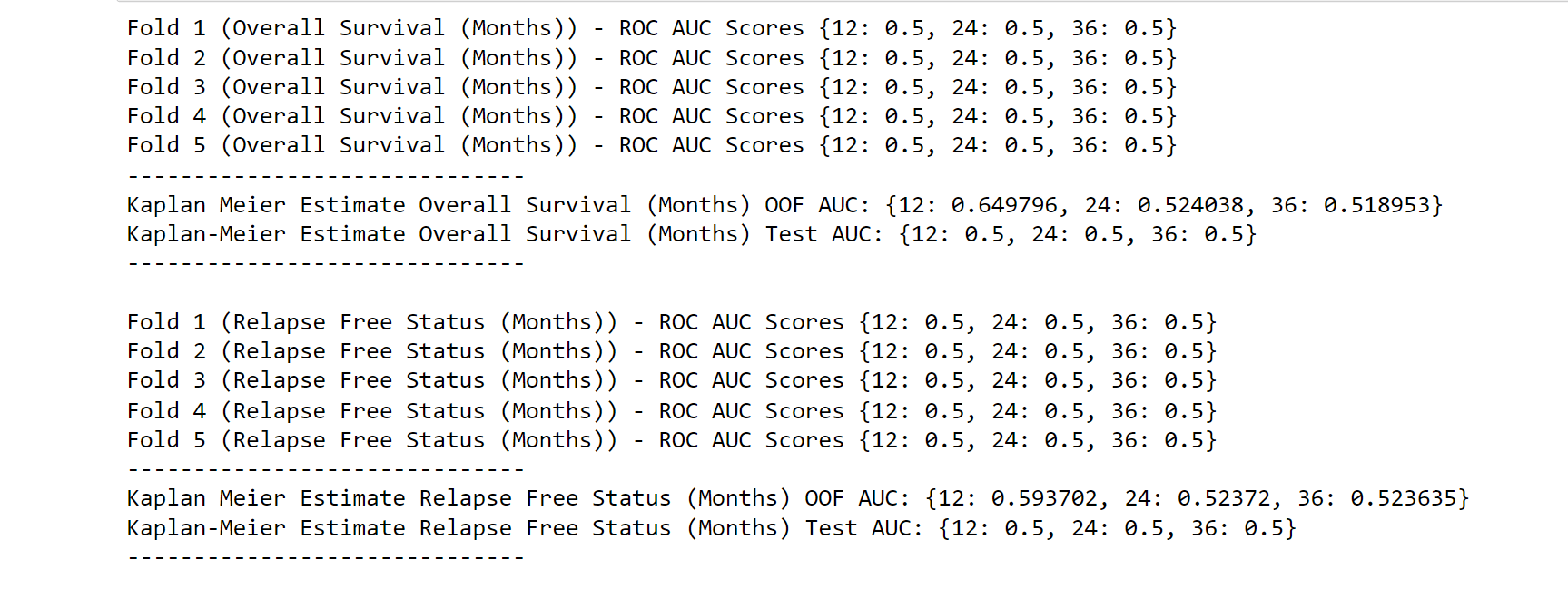

根据结果，我们可以看到，在一年内，生存率为 0.649796、0.524038 和 0.518953。

结论

使用机器学习进行生存分析是一种有前途的方法，可以帮助揭示数据中隐藏的模式并做出更准确的预测。虽然这种方法存在一些挑战，但机器学习技术的进步和计算能力的提升使其越来越可行。