连续值预测

主题

附加文件中包含以下主题和子主题

1. 机器学习中的要素

• 数据
• 训练数据
• 特点
• 算法
• 模型评估
• 超参数调优
• 欠拟合和过拟合
• 部署
• 伦理考量

2. 回归

• 各种回归
• 模型评估
• 假设
• 应用
• 正则化

3. 回归类型详解

• 简单线性回归
  
  • 重要公式
  • 示例说明
• 岭回归
  
  • 重要公式
  • 示例说明
• Lasso 回归
  
  • 重要公式
  • 示例说明
• 多元线性回归
  
  • 重要公式
  • 示例说明
• 多项式回归
  
  • 重要公式
  • 示例说明
• 逻辑回归
  
  • 重要公式
  • 示例说明

4. 结论

现在，让我们深入探讨每个主题

机器学习

机器学习就是让机器像人类一样学习。有许多技术可以帮助我们训练模型并按要求运行。

机器学习中的要素

以下是一些基本的机器学习概念和要素

1. 数据
   机器学习算法主要依赖数据来学习和产生预测。这些信息可以是无结构（如文本、图形或音频）的，也可以是结构化（如表格数据）的。
2. 训练数据
   训练机器学习模型需要有标签的数据集。这意味着数据包含已知正确答案或结果的示例。模型从这些数据中学习，以便对新的、未见过的数据进行预测。
3. 特点
   模型用于做出预测的具体数据点被称为特征。选择和修改数据中相关特征的过程称为特征工程。
4. 算法
   存在不同的机器学习算法，每种算法都是为特定类别的问​​题而设计的。其中包括但不限于强化学习、无监督学习和监督学习。
   监督学习通过在有标签数据上训练模型，教它根据输入-输出对来预测结果。决策树、支持向量机和神经网络是常见算法的示例。
   无监督学习使用无标签数据，并专注于寻找数据中的结构或模式。无监督学习任务的例子包括聚类和降维。
   强化学习的目标是教会代理人在给定环境中做出了一系列决策，以最大化奖励。它经常用于机器人和游戏应用。
5. 模型评估
   在训练机器学习模型后，根据准确率、精确率、召回率、F1分数或均方误差等度量标准评估其性能至关重要，具体取决于问题的性质。
6. 超参数调优
   机器学习模型的超参数是在训练之前设置的，而不是从数据中学习的。找到优化模型性能的理想超参数集称为超参数调优。
7. 欠拟合和过拟合
   过拟合发生在模型过度学习训练集，而在全新、未尝试过的数据上表现不佳。另一方面，欠拟合发生在模型过于简单，无法识别数据中的潜在趋势时。
8. 部署
   一旦机器学习模型经过训练和验证，就可以将其应用于实际应用，包括推荐系统、欺诈检测、自然语言处理、计算机视觉和自动驾驶汽车。
9. 伦理考量
   在数据和算法的偏见、隐私、透明度和公平性方面，机器学习也带来了伦理和社会问题。如果我们希望负责任地创建人工智能，解决这些问题至关重要。

机器学习是一个快速发展的领域，在经济的各个部门都有广泛的应用，包括营销、银行和医疗保健。它能够从根本上改变我们处理和应用数据以应对挑战性问题并做出明智决策的方式。

回归

回归是统计学和机器学习中用于建模和分析变量之间关系的基本工具。它主要用于根据一个或多个输入因子（自变量）预测一个连续结果变量（因变量），这些因子可以是连续的或分类的。

回归分析的主要目标是找到最佳拟合线或曲线，该曲线或曲线说明了自变量和因变量之间的关系。这个线或曲线被称为回归模型。一旦模型在历史数据上进行了训练，就可以应用它来预测新数据或估计因变量的值。

回归的主要特点如下

让我们来看一下回归的一些特点以及回归主题中涉及的类型

各种回归

首先，让我们看一下不同类型的回归

1. 线性回归

• 线性回归假定因变量与一个或多个自变量之间存在线性关系。为了最小化预测值与实际值之间的平方差之和，会寻找一条直线。线性回归有两种类型：岭回归和 Lasso 回归，它们提供正则化以避免过拟合。

2. 多元线性回归

• 当存在多个自变量时，多元线性回归用于建模它们之间的关系。这些变量线性组合形成方程。

3. 多项式回归

• 当变量之间的关系不严格线性时，此方法将多项式曲线拟合到数据。

4. 逻辑回归

• 尽管名称如此，逻辑回归用于分类任务，其中因变量是二元的（例如，是/否，0/1）。它模拟二元结果的概率。

模型评估

• 在回归分析中，通常使用均方误差 (MSE)、均方根误差 (RMSE)、平均绝对误差 (MAE) 或 R 平方（决定系数）等度量标准来评估模型质量。
• 可以使用交叉验证方法，通过不同的数据子集来评估模型的有效性。

假设

• 线性回归的假设是自变量与因变量之间的关系是线性的。
• 此外，它假定误差（或残差）是规律分布的、同方差的，并且彼此独立。

应用

• 回归分析在经济学、金融学、社会科学、工程学和机器学习等众多学科中都有应用。
• 预测股票价格、估算房屋价值、检查营销活动对销售的影响以及模拟自变量与健康结果之间的关系是常见的应用示例。

正则化

• 通过在回归方程中添加惩罚项，岭回归和 Lasso 回归等正则化方法可避免过拟合。
• 与 Lasso 回归（添加基于系数绝对值的惩罚项）不同，岭回归添加基于系数平方和的惩罚项。

回归分析是一种强大的方法，可以从真实世界的数据中提取见解，分析和建模数据中的关系，并进行预测。它在统计学和机器学习等广泛领域都有许多应用。

回归类型详解

让我们深入研究每种回归类型，以便更好地理解每种回归模型。

1. 简单线性回归

简单线性回归是一种统计技术，它涉及将线性方程拟合到观测数据，以表示单个因变量（目标）与单个自变量（预测变量或特征）之间的关系。假定自变量和因变量之间存在线性关系。模型方程的形式如下：

Y = B₀ + B₁X + ε

其中

目标（因变量）是 Y。

自变量（特征或预测变量）是 X。

截距（X 为 0 时 Y 的值）等于 B0。

斜率，即 X 变化一个单位时 Y 的变化量，是 B1。

误差项（实际值与期望值之间的差异）用符号表示。

简单线性回归，有时也称为最小二乘法，旨在预测 B0 和 B1 的值，以最小化误差平方和 (SSE)。

简单线性回归公式

让我们看一下在线性回归工作中用到的一些最重要公式。

1. β₀ 和 β₁ 的估计
   β₁ (斜率) = Σ((Xᵢ - Mean(X)) * (Yᵢ - Mean(Y))) / Σ((Xᵢ - Mean(X)²)
   β₀ (截距) = Mean(Y) - β₁ * Mean(X)
2. 给定 X 时 Y 的预测
   Ŷ = β₀ + β₁X
3. 残差（误差）
   残差 (εᵢ) = Yᵢ - Ŷᵢ
4. 误差平方和 (SSE)
   SSE = Σ(εᵢ²)
5. 决定系数 (R²)
   R² = 1 - (SSE / SST)，其中 SST 是总平方和。

示例

让我们通过一个简单例子来说明简单线性回归，根据学习时间（X）预测学生的期末考试成绩（Y）。

假设您拥有以下数据集

1. 计算 X 和 Y 的均值

Mean(X) = (2 + 3 + 4 + 5 + 6) / 5 = 4

Mean(Y) = (65 + 75 + 82 + 88 + 92) / 5 = 80.4

2. 使用公式计算斜率 (β₁)

β₁ = Σ((Xᵢ - Mean(X)) * (Yᵢ - Mean(Y))) / Σ((Xᵢ - Mean(X)²)

β₁ = ((2-4)(65-80.4) + (3-4)(75-80.4) + (4-4)(82-80.4) + (5-4)(88-80.4) + (6-4)*(92-80.4)) / ((2-4)² + (3-4)² + (4-4)² + (5-4)² + (6-4)²)

β₁ ≈ 5.52

3. 使用公式计算截距 (β₀)

β₀ = Mean(Y) - β₁ * Mean(X)

β₀ ≈ 80.4 - 5.52 * 4

β₀ ≈ 57.28

4. 线性回归方程为

Y = 57.28 + 5.52X

现在，您可以根据学习时间来应用此方程来预测您的期末考试成绩。

通过在线性回归方程中加入正则化项，线性回归中的岭回归和 Lasso 回归方法可以解决多重共线性问题并防止过拟合。下面将详细介绍这两种方法及其公式和示例

岭回归

通过在线性回归方程中加入正则化项，线性回归中的岭回归和 Lasso 回归方法可以解决多重共线性问题并防止过拟合。下面将详细介绍这两种方法及其公式和示例

岭目标函数 = SSE (误差平方和) + λ * Σ(βᵢ²)

其中

在进行简单线性或多元线性回归时，使用 SSE，即误差平方和。

正则化参数，即 λ（lambda），控制正则化的强度。

Σ(βᵢ²) 表示系数平方和。

岭回归试图最小化此目标函数。

示例

假设您使用岭回归来预测房屋价格，使用两个预测变量：面积（X1）和卧室数量（X2）。

与多元线性回归类似，岭回归方程也包含一个正则化项

Y = β₀ + β₁X₁ + β₂X₂ + λΣ(βᵢ²)

可以使用此方程在估计系数 β₀、β₁ 和 β₂ 的同时最小化目标函数。

Lasso 回归

另一种在線性回归方程中包含惩罚项的方法是 Lasso 回归，有时也称为 L1 正则化。与岭回归不同，Lasso 通过将某些系数降至零来促进模型稀疏性。Lasso 回归的更新目标函数如下：

Lasso 目标函数 = SSE + λ * Σ|βᵢ|

其中

在进行简单线性或多元线性回归时，使用 SSE，即误差平方和。

正则化参数，用 λ（lambda）表示，控制正则化的程度。

Σ|βᵢ| 表示系数绝对值之和。

Lasso 回归尝试最小化此目标函数，同时可能将某些系数降至零。

示例

使用与预测房屋价格（包括面积 X1 和卧室数量 X2 作为预测变量）相同的示例，Lasso 回归方程如下：

Y = β₀ + β₁X₁ + β₂X₂ + λΣ|βᵢ|

可以使用此方程在估计系数 β₀、β₁ 和 β₂ 的同时最小化目标函数。Lasso 可能将某些系数精确设置为零，从而仅为模型选择最重要的预测变量。

在实际应用中，通常使用交叉验证等方法将正则化参数设置为一个能最佳平衡模型复杂度和拟合优度的值。岭回归和 Lasso 回归是用于处理多重共线性和避免线性回归模型过拟合的有用方法。

2. 多元线性回归

多元线性回归是简单线性回归的扩展，它涉及将线性方程拟合到观测数据，以表示因变量（目标）与两个或多个自变量（预测变量或特征）之间的关系。在多元线性回归中，模型的方程形式如下：

Y = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ + ε

其中

目标（因变量）是 Y。

自变量（预测变量或特征）是 X1、X2、... 和 Xp。

截距是 β₀。

自变量的系数是 β₀、β₁、β₂、...、βₚ。

误差项（实际值与期望值之间的差异）用符号表示。

与简单线性回归类似，多元线性回归的目标是估计 β₀、β₁、β₂、...、βₚ 的值，以最小化误差平方和 (SSE)。

多元线性回归公式

1. β₀、β₁、β₂、...、βₚ 的估计
   β₀ (截距) = Mean(Y) - (β₁ * Mean(X₁) + β₂ * Mean(X₂) + ... + βₚ * Mean(Xₚ))
   βᵢ (每个特征的系数) = Σ((Xᵢ - Mean(Xᵢ)) * (Y - Ŷ)) / Σ((Xᵢ - Mean(Xᵢ))²) 其中 i = 1, 2, ..., p
2. 给定一组 X₁、X₂、...、Xₚ 时 Y 的预测
   Ŷ = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ
3. 残差（误差）
   残差 (εᵢ) = Yᵢ - Ŷᵢ
4. 误差平方和 (SSE)
   SSE = Σ(εᵢ²)
5. 决定系数 (R²)
   R² = 1 - (SSE / SST)，其中 SST 是总平方和。

示例

让我们通过一个例子来说明多元线性回归，根据房屋面积（X1）和卧室数量（X2）这两个自变量来预测房屋价格（Y）。

假设您拥有以下数据集

计算 X₁、X₂ 和 Y 的均值

Mean(X₁) = (1500 + 2000 + 1800 + 2200 + 1600) / 5 = 1820

Mean(X₂) = (3 + 4 + 3 + 5 + 4) / 5 = 3.8

Mean(Y) = (200,000 + 250,000 + 220,000 + 280,000 + 210,000) / 5 = 232,000

使用公式估计系数（β₀、β₁、β₂）

β₀ (截距) = Mean(Y) - (β₁ * Mean(X₁) + β₂ * Mean(X₂))

β₁（X₁ 的系数）和 β₂（X₂ 的系数）也以类似的方式使用各自的公式进行计算。

多元线性回归方程是

Y = β₀ + β₁X₁ + β₂X₂

现在可以使用此方程来根据房屋面积和卧室数量预测房屋价格。

(4-4)(82-80.4) + (5-4)(88-80.4) + (6-4)*(92-80.4)) / ((2-4)² + (3-4)² + (4-4)² + (5-4)² + (6-4)²)

β₁ ≈ 5.52

5. 使用公式计算截距 (β₀)

β₀ = Mean(Y) - β₁ * Mean(X)

β₀ ≈ 80.4 - 5.52 * 4

β₀ ≈ 57.28

6. 线性回归方程是

Y = 57.28 + 5.52X

现在，您可以根据学习时间来应用此方程来预测您的期末考试成绩。

通过在线性回归方程中加入正则化项，线性回归中的岭回归和 Lasso 回归方法可以解决多重共线性问题并防止过拟合。下面将详细介绍这两种方法及其公式和示例

3. 多项式回归

使用 n 次多项式来表示自变量（预测变量）和因变量（目标）之间关系的回归称为多项式回归。这种线性回归类型使用多项式方程来表示变量之间的关系，而不是线性方程。当变量之间存在弯曲的模式而不是直线时，多项式回归非常有用。

下面给出了多项式回归的定义及其公式和示例

多项式回归公式

多项式回归的方程如下：

Y = β₀ + β₁X + β₂X² + β₃X³ + ... + βₙXⁿ + ε

其中

目标（因变量）是 Y。

X 是一个预测变量，是自变量。

多项式项的系数是 β₀、β₁、β₂、β₃、...、βₙ。

方程中使用的 X 的最高幂次决定了多项式的次数 n。

误差项（实际值与期望值之间的差异）用符号表示。

与线性回归类似，多项式回归的目标是估计 β₀、β₁、β₂、β₃、...、βₙ 的值，以最小化误差平方和 (SSE)。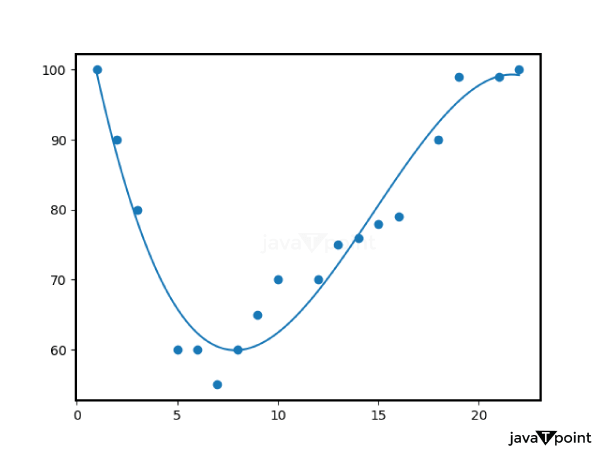

示例

让我们看一个例子，您需要预测一个人的收入（Y）与他们的工作经验年限（X）之间的关系。由于随着经验的增加，薪水往往会更快增长，因此这种关系不是线性的。在这种情况下，多项式回归可能是一个不错的选择。

假设您拥有以下数据集

例如，如果您使用 2 次多项式，那么在使用多项式回归时，您将拟合一个二次方程：

假设您拥有以下数据集

Y = β₀ + β₁X + β₂X² + ε

现在，在最小化 SSE 的同时，使用此方程来估计系数 β₀、β₁ 和 β₂。可以使用各种统计或机器学习方法执行此回归，例如梯度下降或 Python 或 R 中的专用回归库。

在估计了系数后，您可以使用多项式方程进行预测。例如，对于有六年经验的人，薪酬范围如下：

将 X = 6 代入公式

Y = β₀ + β₁(6) + β₂(6²)

要计算 Y，请代入预测的系数。

为了避免模型过拟合或欠拟合数据，选择合适的多项式次数至关重要。多项式回归是一种灵活的技术，可以捕捉变量之间的非线性相关性。

4. 逻辑回归

使用称为逻辑回归的统计方法，可以预测具有两个可能值（通常表示为 0 和 1，例如是/否、垃圾邮件/非垃圾邮件、通过/失败）的分类结果。与其名称的含义相反，逻辑回归是一种分类算法。它通过使用逻辑函数将预测转换为介于 0 和 1 之间的概率，来模拟输入属于特定类别的可能性。

下面给出了逻辑回归的定义及其公式和示例

逻辑回归公式

逻辑（或 Sigmoid）函数用于逻辑回归模型，以模拟因变量（Y）为 1（或属于正类）的概率：

P(Y=1|X) = 1 / (1 + e^(-z))

其中

P(Y=1|X) 是 Y 为 1 的概率，给定输入 X。

自然对数的底数 e，约等于 2.71828。

预测变量线性组合形成 z：z = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ

预测变量 X₁、X₂、...、Xₚ 的系数是 β₀、β₁、β₂、...、βₚ。

为了模拟概率，逻辑函数确保结果被限制在 0 到 1 之间。

通常选择一个决策阈值（例如 0.5）将输入分类到两个类别之一。如果 P(Y=1|X) 大于阈值，则输入被分类为 1；否则，则被分类为 0。

示例

让我们来看一个例子，您想根据学生学习的小时数（X）来预测他们的考试结果，是会通过（1）还是会不及格（0）。

假设您拥有以下数据集

为了预测一个学生投入一定学习时间后是否会通过或不及格，您应该构建一个逻辑回归模型。

• 通过使用优化技术（例如梯度下降）将逻辑回归模型拟合到您的数据，可以估计逻辑回归公式中的系数 0 和 1。
• 一旦模型经过训练，您就可以使用它来预测学生的通过率，具体取决于他们花费的学习时间。
• 您使用估计的概率和阈值（例如 0.5）来将学生分类为通过或不及格。例如，如果预测的概率大于或等于 0.5，则将学生分类为通过（1）；否则，则分类为不及格（0）。

对于二元和多类分类问题，逻辑回归这种分类算法在机器学习中经常被使用。当根据一个或多个预测因子对事件发生的可能性进行建模时，它尤其有用。

结论

回归是机器学习中用于建模和预测连续结果的基本方法，它基于变量之间的关系。它包括一系列方法，从简单的线性回归到更复杂的方法，如多项式回归、岭回归和 Lasso 回归。这些技术使我们能够衡量和分析预测因子对目标变量的影响，从而为金融、医疗保健、营销等众多领域提供重要的见解。由于其易于理解的特性，回归模型作为理解数据关系和进行预测的工具而备受重视。

此外，回归方法通常需要进行彻底的特征工程和数据预处理才能产生可靠的结果。回归的关键模型选择和评估过程涉及选择最佳回归策略，并使用 MSE 和 R2 等指标进行验证。回归是机器学习工具包中一种灵活且应用广泛的方法，它使数据科学家和分析师能够创建预测模型，从而在各种领域改进决策流程。