深度参数化连续卷积神经网络

参数化连续卷积是一种创新的可学习算子，它适用于非网格结构数据。其主要概念是利用参数化核函数覆盖整个连续向量空间。Uber 高级技术组的研究人员提出了深度参数化连续核卷积。简单的 CNN 架构假定网格状布局，并使用离散卷积作为其核心构建组件，这是本文的驱动力。这使得它们难以对众多实际应用进行精确卷积。因此，他们提出了一种称为参数化连续卷积的卷积技术。

参数化连续卷积

通过使用覆盖整个连续向量空间的参数化核，参数化连续卷积是一种可学习的算子，它作用于非网格组织数据。如果支持结构是可计算的，它可以处理任何数据结构。通过使用蒙特卡洛采样，连续卷积算子可以大致与离散卷积进行比较。

但是，我们如何创建连续卷积核函数 g 呢？该函数 g 被参数化以赋予支持域中的每个点一个值（核权重）。对于连续卷积，这种参数化是不可能的，因为函数 g 将在无限数量的点上指定。

多层感知器 (MLP) 具有表达能力，能够近似连续函数。因此，解决该问题的方法是使用连续参数函数对 g 进行建模。

核函数 g(z) 由有限的参数集指定，涵盖整个连续支持域。

连续参数化卷积层

参数化连续卷积层可以有不同的输入和输出。每个卷积层的输入由以下三个组件组成

• 特征向量输入 (F)
• 支持域中的相应位置 (S = Yj)
• 输出域的位置 (0 = Xi)

我们评估每个层中所有 Xi in S 和所有 Yj in O 的核函数 g(Yj - Xi;)。最终的输出特征确定如下

其中，

• N: 输入点的数量
• M: 总输出点数。
• D: 支持域的维度为 D。
• F: 输出特征的维度
• 0: 输入的特征维度为 0。

架构

输入特征及其在支持域中的位置作为输入提供给网络。我们可以添加批量归一化、非线性和层之间的剩余连接，这对于帮助收敛至关重要，以构建传统的 CNN 架构。通过使用池化可以在支持域中收集信息。

由于所有块都是可微分的，因此可以使用反向传播来训练网络。

强制局部性持续卷积。

为了保持局部性，传统的卷积核尺寸较小。通过参数化连续卷积也可以强制限制函数 g 对 x 附近点的影响。因此，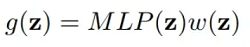

在调制窗口 (w) 中，我们只能保留 K 近邻 (kNN) 或设定半径内的点的非零核值（球点）。

分析