决策树分类算法

• 决策树是一种监督学习技术，可用于分类和回归问题，但主要用于解决分类问题。它是一种树状结构的分类器，其中内部节点表示数据集的特征，分支表示决策规则，而每个叶节点表示结果。
• 在决策树中，有两个节点，即决策节点和叶节点。决策节点用于做出任何决策并具有多个分支，而叶节点是这些决策的结果，不包含任何进一步的分支。
• 决策或测试是基于给定数据集的特征进行的。
• 它是用于根据给定条件获得问题/决策所有可能解决方案的图形表示。
• 之所以称为决策树，是因为它与树相似，从根节点开始，然后扩展到进一步的分支并构建树状结构。
• 为了构建树，我们使用CART 算法，它代表分类和回归树算法。
• 决策树简单地提出一个问题，并根据答案（是/否），它进一步将树分割成子树。
• 下图解释了决策树的一般结构

注意：决策树可以包含分类数据（是/否）和数值数据。

为什么要使用决策树？

机器学习中有各种算法，因此选择最适合给定数据集和问题的算法是创建机器学习模型时要记住的主要一点。以下是使用决策树的两个原因：

• 决策树通常模仿人类在做决定时的思维能力，因此易于理解。
• 决策树背后的逻辑易于理解，因为它显示了树状结构。

决策树术语

决策树算法如何工作？

在决策树中，为了预测给定数据集的类别，算法从树的根节点开始。该算法将根属性的值与记录（实际数据集）属性进行比较，并根据比较结果沿着分支跳转到下一个节点。

对于下一个节点，算法再次将属性值与不同的子节点进行比较并进一步移动。它继续这个过程，直到到达树的叶节点。可以使用以下算法更好地理解完整的过程：

• 步骤 1：用根节点 S 开始树，S 包含完整的数据集。
• 步骤 2：使用属性选择度量 (ASM) 查找数据集中的最佳属性。
• 步骤 3：将 S 分割成包含最佳属性的可能值的子集。
• 步骤 4：生成包含最佳属性的决策树节点。
• 步骤 5：使用步骤 3 中创建的数据集子集递归地创建新的决策树。继续此过程，直到达到无法进一步分类节点的阶段，并将最终节点称为叶节点。

示例：假设有一位候选人收到了工作机会，并想决定是否接受。因此，为了解决这个问题，决策树从根节点（由 ASM 的薪资属性）开始。根节点根据相应的标签进一步分裂成下一个决策节点（到办公室的距离）和一个叶节点。下一个决策节点进一步分裂成一个决策节点（出租车服务）和一个叶节点。最后，决策节点分裂成两个叶节点（接受的报价和拒绝的报价）。请参考下图

属性选择度量

在实现决策树时，主要问题是如何为根节点和子节点选择最佳属性。因此，为了解决这类问题，有一种技术称为属性选择度量或 ASM。通过这种度量，我们可以轻松地为树的节点选择最佳属性。ASM 有两种流行技术，它们是：

• 信息增益 (Information Gain)
• 基尼指数

1. 信息增益

• 信息增益是根据属性分割数据集后熵变化的度量。
• 它计算了特征为我们提供了一个类别的多少信息。
• 根据信息增益的值，我们分割节点并构建决策树。
• 决策树算法始终尝试最大化信息增益值，信息增益最高的节点/属性将首先被分割。它可以使用以下公式计算：

熵：熵是衡量给定属性中不纯度的度量。它表示数据的随机性。熵可以计算为：

Entropy(s)= -P(yes)log2 P(yes)- P(no) log2 P(no)

其中，

• S = 样本总数
• P(yes) = 是的概率
• P(no) = 否的概率

2. 基尼指数

• 基尼指数是 CART（分类和回归树）算法在创建决策树时使用的不纯度或纯度度量。
• 与高基尼指数相比，低基尼指数的属性应该受到青睐。
• 它只创建二元分裂，CART 算法使用基尼指数来创建二元分裂。
• 基尼指数可以使用以下公式计算：

Gini Index= 1- ∑jPj2

剪枝：获得最优决策树

剪枝是从树中删除不必要节点的過程，以获得最优决策树。

太大的树会增加过拟合的风险，而太小的树可能无法捕获数据集的所有重要特征。因此，一种在不降低准确性的情况下减小学习树大小的技术称为剪枝。主要有两种树剪枝技术：

• 成本复杂度剪枝
• 减少错误剪枝。

决策树的优点

• 它易于理解，因为它遵循人类在现实生活中做任何决定时所遵循的相同过程。
• 它对于解决决策相关问题非常有用。
• 它有助于思考问题的所有可能结果。
• 与其他算法相比，数据清理的需求较少。

决策树的缺点

• 决策树包含许多层，这使其变得复杂。
• 它可能存在过拟合问题，可以通过随机森林算法解决。
• 对于更多的类别标签，决策树的计算复杂度可能会增加。

决策树的 Python 实现

现在我们将使用 Python 实现决策树。为此，我们将使用我们在之前的分类模型中使用的“user_data.csv”数据集。通过使用相同的数据集，我们可以将决策树分类器与其他分类模型进行比较，例如KNN SVM、LogisticRegression 等。

步骤也将保持不变，如下所示：

• 数据预处理步骤
• 将决策树算法拟合到训练集
• 预测测试结果
• 测试结果的准确性（创建混淆矩阵）
• 可视化测试集结果。

1. 数据预处理步骤

预处理步骤的代码如下：

在上面的代码中，我们对数据进行了预处理。其中我们加载了数据集，如下所示：

2. 将决策树算法拟合到训练集

现在我们将模型拟合到训练集。为此，我们将从 sklearn.tree 库导入 DecisionTreeClassifier 类。代码如下：

在上面的代码中，我们创建了一个分类器对象，其中我们传递了两个主要参数：

• “criterion='entropy'”： Criterion 用于衡量分割的质量，该质量通过熵提供的信息增益来计算。
• random_state=0"：用于生成随机状态。

下面的输出是：

Out[8]: 
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
                       random_state=0, splitter='best')

3. 预测测试结果

现在我们将预测测试集结果。我们将创建一个新的预测向量 y_pred。代码如下：

输出

在下面的输出图像中，给出了预测输出和实际测试输出。我们可以清楚地看到预测向量中存在一些值，它们与实际向量值不同。这些是预测错误。

4. 测试结果的准确性（创建混淆矩阵）

在上面的输出中，我们看到存在一些错误的预测，所以如果我们想知道正确和错误预测的数量，我们需要使用混淆矩阵。代码如下：

输出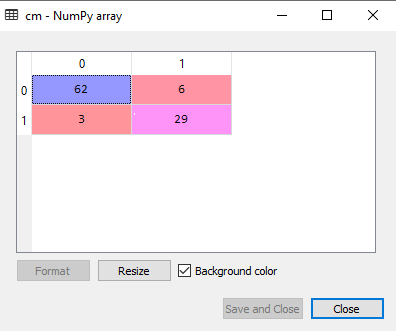

在上面的输出图像中，我们可以看到混淆矩阵，它有6+3=9 次错误预测，62+29=91 次正确预测。因此，我们可以说，与其它分类模型相比，决策树分类器做出了一个不错的预测。

5. 可视化训练集结果

在这里，我们将可视化训练集结果。为了可视化训练集结果，我们将为决策树分类器绘制一个图。分类器将预测购买或未购买 SUV 汽车的用户的“是”或“否”，就像我们在逻辑回归中所做的那样。代码如下：

输出

上面的输出与其他分类模型完全不同。它既有垂直线又有水平线，这些线根据年龄和估计的薪资变量分割了数据集。

正如我们所见，树试图捕获每个数据集，这是过拟合的情况。

6. 可视化测试集结果

测试集结果的可视化将与训练集的可视化相似，只是训练集将被替换为测试集。

输出

如上图所示，在紫色区域内有一些绿色数据点，反之亦然。所以，这些是我们曾在混淆矩阵中讨论过的错误预测。

关于决策树分类算法的选择题练习

1. 基尼指数使用什么标准来确定决策树中节点的纯度？

1. 熵
2. 变化
3. 类别概率之间的平方差
4. 平均数

2. 以下哪种剪枝技术常用于避免决策树的过拟合？

1. 叶节点剪枝
2. 随机剪枝
3. 预剪枝和后剪枝
4. 基尼剪枝

3. 断言 (A)：决策树容易过拟合。

原因 (R)：决策树可以通过分割数据以完美匹配所有训练点来创建过于复杂的模型。

选项

1. A 和 R 都为真，并且 R 是 A 的正确解释。
2. A 和 R 都为真，但 R 不是 A 的正确解释。
3. A 为真，但 R 为假。
4. A 为假，但 R 为真。

4. 在决策树中，更高的信息增益表明某个特征具有什么特点？

1. 该特征有更多缺失值
2. 该特征能更好地分离类别
3. 该特征不太相关
4. 该特征有更多实例

5. 在决策树的背景下，使用随机森林的目的是什么？

1. 简化模型
2. 降低计算复杂度
3. 降低方差并提高泛化能力
4. 增加偏差