多元线性回归

2025年3月17日 | 阅读 7 分钟

在前面的主题中，我们学习了简单线性回归，其中使用单个独立/预测（X）变量来建模响应变量（Y）。但是，在某些情况下，响应变量可能受到多个预测变量的影响；对于这种情况，使用多元线性回归算法。

此外，多元线性回归是简单线性回归的扩展，因为它使用多个预测变量来预测响应变量。我们可以将其定义为

多元线性回归是重要的回归算法之一，它对单个因变量（连续变量）与多个自变量之间的线性关系进行建模。

示例

根据汽车的发动机尺寸和气缸数量预测二氧化碳排放量。

MLR 的一些关键点

对于 MLR，因变量或目标变量（Y）必须是连续/实数，但预测变量或自变量可以是连续或类别形式。
每个特征变量必须与因变量建模线性关系。
MLR 尝试通过数据点的多维空间拟合一条回归线。

MLR 方程

在多元线性回归中，目标变量（Y）是多个预测变量 x₁、x₂、x₃、...、x_n 的线性组合。由于它是简单线性回归的增强，因此多元线性回归方程也适用，方程变为

Y= b<sub>0</sub>+b<sub>1</sub>x<sub>1</sub>+ b<sub>2</sub>x<sub>2</sub>+ b<sub>3</sub>x<sub>3</sub>+...... bnxn       ............... (a)

其中，

Y= 输出/响应变量

b₀、b₁、b₂、b₃、b_n....= 模型的系数。

x₁、x₂、x₃、x₄,...= 各种独立/特征变量

多元线性回归的假设

目标变量和预测变量之间应存在线性关系。
回归残差必须正态分布。
MLR 假设数据中很少或没有多重共线性（自变量之间的相关性）。

使用 Python 实现多元线性回归模型

要使用 Python 实现 MLR，我们有以下问题

问题描述

我们有一个包含50 家初创公司的数据集。该数据集包含五个主要信息：研发支出、行政支出、营销支出、州和一年内的利润。我们的目标是创建一个模型，可以轻松确定哪家公司利润最高，以及哪个是影响公司利润的最主要因素。

由于我们需要找到利润，所以它是因变量，其他四个变量是自变量。以下是部署 MLR 模型的主要步骤

数据预处理步骤
将 MLR 模型拟合到训练集
预测测试集的结果

步骤 1：数据预处理步骤

第一步是数据预处理，我们已在本教程中讨论过。此过程包含以下步骤

导入库： 首先，我们将导入有助于构建模型的库。以下是其代码

# importing libraries
import numpy as nm
import matplotlib.pyplot as mtp
import pandas as pd

导入数据集： 现在我们将导入包含所有变量的数据集（50_CompList）。以下是其代码

#importing datasets
data_set= pd.read_csv('50_CompList.csv')

输出： 我们将得到数据集为

在上面的输出中，我们可以清楚地看到有五个变量，其中四个是连续变量，一个是类别变量。

提取因变量和自变量

#Extracting Independent and dependent Variable
x= data_set.iloc[:, :-1].values
y= data_set.iloc[:, 4].values

输出

输出 [5]

array([[165349.2, 136897.8, 471784.1, 'New York'],
       [162597.7, 151377.59, 443898.53, 'California'],
       [153441.51, 101145.55, 407934.54, 'Florida'],
       [144372.41, 118671.85, 383199.62, 'New York'],
       [142107.34, 91391.77, 366168.42, 'Florida'],
       [131876.9, 99814.71, 362861.36, 'New York'],
       [134615.46, 147198.87, 127716.82, 'California'],
       [130298.13, 145530.06, 323876.68, 'Florida'],
       [120542.52, 148718.95, 311613.29, 'New York'],
       [123334.88, 108679.17, 304981.62, 'California'],
       [101913.08, 110594.11, 229160.95, 'Florida'],
       [100671.96, 91790.61, 249744.55, 'California'],
       [93863.75, 127320.38, 249839.44, 'Florida'],
       [91992.39, 135495.07, 252664.93, 'California'],
       [119943.24, 156547.42, 256512.92, 'Florida'],
       [114523.61, 122616.84, 261776.23, 'New York'],
       [78013.11, 121597.55, 264346.06, 'California'],
       [94657.16, 145077.58, 282574.31, 'New York'],
       [91749.16, 114175.79, 294919.57, 'Florida'],
       [86419.7, 153514.11, 0.0, 'New York'],
       [76253.86, 113867.3, 298664.47, 'California'],
       [78389.47, 153773.43, 299737.29, 'New York'],
       [73994.56, 122782.75, 303319.26, 'Florida'],
       [67532.53, 105751.03, 304768.73, 'Florida'],
       [77044.01, 99281.34, 140574.81, 'New York'],
       [64664.71, 139553.16, 137962.62, 'California'],
       [75328.87, 144135.98, 134050.07, 'Florida'],
       [72107.6, 127864.55, 353183.81, 'New York'],
       [66051.52, 182645.56, 118148.2, 'Florida'],
       [65605.48, 153032.06, 107138.38, 'New York'],
       [61994.48, 115641.28, 91131.24, 'Florida'],
       [61136.38, 152701.92, 88218.23, 'New York'],
       [63408.86, 129219.61, 46085.25, 'California'],
       [55493.95, 103057.49, 214634.81, 'Florida'],
       [46426.07, 157693.92, 210797.67, 'California'],
       [46014.02, 85047.44, 205517.64, 'New York'],
       [28663.76, 127056.21, 201126.82, 'Florida'],
       [44069.95, 51283.14, 197029.42, 'California'],
       [20229.59, 65947.93, 185265.1, 'New York'],
       [38558.51, 82982.09, 174999.3, 'California'],
       [28754.33, 118546.05, 172795.67, 'California'],
       [27892.92, 84710.77, 164470.71, 'Florida'],
       [23640.93, 96189.63, 148001.11, 'California'],
       [15505.73, 127382.3, 35534.17, 'New York'],
       [22177.74, 154806.14, 28334.72, 'California'],
       [1000.23, 124153.04, 1903.93, 'New York'],
       [1315.46, 115816.21, 297114.46, 'Florida'],
       [0.0, 135426.92, 0.0, 'California'],
       [542.05, 51743.15, 0.0, 'New York'],
       [0.0, 116983.8, 45173.06, 'California']], dtype=object)

正如我们在上面的输出中看到的那样，最后一列包含类别变量，不适合直接用于模型拟合。因此，我们需要对该变量进行编码。

编码虚拟变量

由于我们有一个类别变量（州），不能直接应用于模型，因此我们将对其进行编码。要将类别变量编码为数字，我们将使用 LabelEncoder 类。但这还不够，因为它仍然具有一些关系顺序，可能会创建错误的模型。因此，为了解决这个问题，我们将使用 OneHotEncoder，它将创建虚拟变量。以下是其代码

#Catgorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_x= LabelEncoder()
x[:, 3]= labelencoder_x.fit_transform(x[:,3])
onehotencoder= OneHotEncoder(categorical_features= [3])  
x= onehotencoder.fit_transform(x).toarray()

这里我们只编码一个自变量，即州，因为其他变量是连续的。

输出

正如我们在上面的输出中看到的，州列已转换为虚拟变量（0 和 1）。这里每个虚拟变量列对应一个州。我们可以通过将其与原始数据集进行比较来检查。第一列对应于加利福尼亚州，第二列对应于佛罗里达州，第三列对应于纽约州。

注意：我们不应该同时使用所有虚拟变量，因此它必须比虚拟变量的总数少 1，否则会产生虚拟变量陷阱。

现在，我们只编写一行代码来避免虚拟变量陷阱

#avoiding the dummy variable trap:
x = x[:, 1:]

如果我们不删除第一个虚拟变量，它可能会在模型中引入多重共线性。

正如我们在上面的输出图像中看到的，第一列已被删除。

现在我们将数据集分成训练集和测试集。其代码如下

# Splitting the dataset into training and test set.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.2, random_state=0)

上述代码会将我们的数据集分成训练集和测试集。

输出： 上述代码会将数据集分成训练集和测试集。您可以通过单击 Spyder IDE 中给出的变量资源管理器选项来检查输出。测试集和训练集将如下图所示

测试集

训练集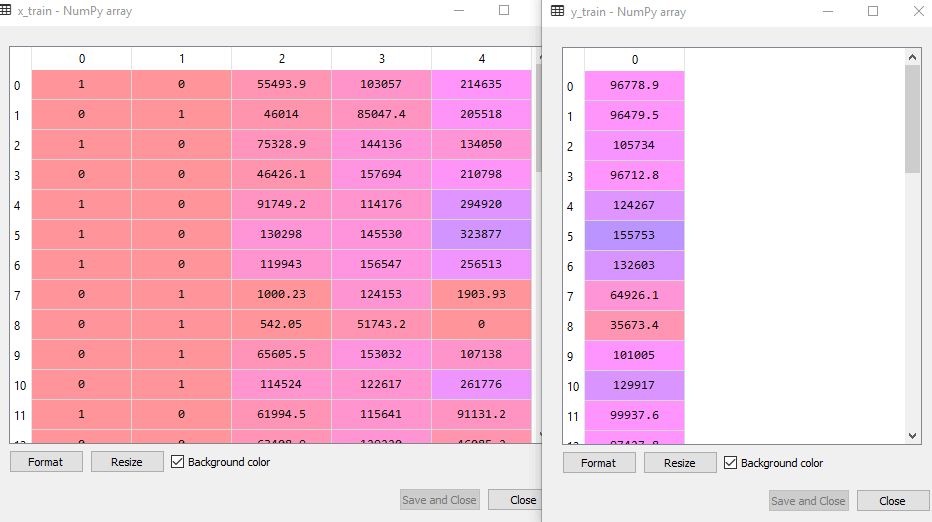

注意：在 MLR 中，我们不会进行特征缩放，因为它由库负责，因此我们无需手动进行。

步骤 2：将我们的 MLR 模型拟合到训练集

现在，我们已经很好地准备了数据集以进行训练，这意味着我们将把我们的回归模型拟合到训练集。这与我们在简单线性回归模型中所做类似。其代码将是

#Fitting the MLR model to the training set:
from sklearn.linear_model import LinearRegression
regressor= LinearRegression()
regressor.fit(x_train, y_train)

输出

Out[9]: LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

现在，我们已使用训练数据集成功训练了模型。在下一步中，我们将使用测试数据集测试模型的性能。

步骤 3：预测测试集结果

我们模型的最后一步是检查模型的性能。我们将通过预测测试集结果来完成。为了进行预测，我们将创建一个 y_pred 向量。以下是其代码

#Predicting the Test set result;
y_pred= regressor.predict(x_test)

通过执行上述代码行，将在变量资源管理器选项下生成一个新的向量。我们可以通过比较预测值和测试集值来测试我们的模型。

输出

在上面的输出中，我们有预测结果集和测试集。我们可以通过逐个索引比较这两个值来检查模型性能。例如，第一个索引的预测利润值为 103015$，测试/实际利润值为 103282$。差异仅为 267$，这是一个很好的预测，因此，我们的模型在此处最终完成。

我们还可以检查训练数据集和测试数据集的分数。以下是其代码

print('Train Score: ', regressor.score(x_train, y_train))
print('Test Score: ', regressor.score(x_test, y_test))

输出： 分数是

Train Score:  0.9501847627493607
Test Score:  0.9347068473282446

上述分数表明我们的模型在训练数据集上准确率为 95%，在测试数据集上准确率为 93%。

注意：在下一个主题中，我们将看到如何使用向后消除过程来提高模型的性能。

多元线性回归的应用

多元线性回归主要有两个应用

自变量对预测的有效性
预测变化的影响

下一个主题向后消除

← 上一个下一个 →

我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题

联系信息

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

hr@tpointtech.com

+91-9599086977

关注我们

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

机器学习

监督式学习

分类

杂项

相关教程

面试题

多元线性回归

MLR 方程

多元线性回归的假设

使用 Python 实现多元线性回归模型

注意： 我们不应该同时使用所有虚拟变量，因此它必须比虚拟变量的总数少 1，否则会产生虚拟变量陷阱。

注意： 在 MLR 中，我们不会进行特征缩放，因为它由库负责，因此我们无需手动进行。

步骤 2：将我们的 MLR 模型拟合到训练集

步骤 3：预测测试集结果

注意： 在下一个主题中，我们将看到如何使用向后消除过程来提高模型的性能。

多元线性回归的应用

相关帖子

回归分析

简单线性回归

多项式回归

向后消除

机器学习中的线性回归

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器

注意：我们不应该同时使用所有虚拟变量，因此它必须比虚拟变量的总数少 1，否则会产生虚拟变量陷阱。

注意：在 MLR 中，我们不会进行特征缩放，因为它由库负责，因此我们无需手动进行。

注意：在下一个主题中，我们将看到如何使用向后消除过程来提高模型的性能。