机器学习多项式回归

多项式回归是线性回归的一种变体，其中自变量 (x) 和因变量 (y) 之间的依赖关系被建模为 n 次多项式。特别适用于对数据中的非线性趋势进行建模，因为它能更好地建模曲线关系。

为什么选择多项式回归？

非线性关系

当自变量（输入）和因变量（输出）之间的交互是非线性时，可以使用多项式回归。它可以考虑到数据中的曲线，而线性回归只能拟合一条直线。

更适合曲线数据

在曲线关系的情况下，项以多项式的形式包含在内。拟合不佳通常表示残差具有明显的模式。多项式回归有助于捕获此类非线性趋势。

灵活性和复杂性

多项式回归也更灵活，因为它能够拥有表示复杂曲线效应的高阶项。它超越了完全独立变量的前提，并适应更复杂的数据形式。

多项式回归过程如何工作？

多项式回归通过在模型中包含更高次项来捕获任何非线性效应，从而扩展了线性回归。n 次多项式回归的一般公式是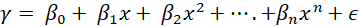

其中

• y 是因变量
• x 是自变量
• β₀, β₁, …, βₙ 是多项式项的系数
• n 是多项式的次数
• ε 是误差项

其转换是根据 x 建立 y 的期望值。在简单线性回归中，关系表示为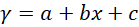

其中 和 分别是截距和斜率，e 是误差。但在非线性关系的情况下（例如，当使用温度建模化学合成过程时），使用直线表示趋势。通过在多项式回归中引入高阶项，即 x 2、x 3 等，来解决这个问题。

例如：二次模型的形式是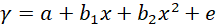

这使得模型能够描绘曲线关系。更一般地，多项式回归可以提高到 n 次幂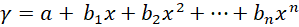

无论方程与 x 的幂次最终变得多么笨拙，回归在其系数 (b 0, b 1, …, b n) 方面仍然是线性的。确定这些系数的方法通常通过最小二乘法导出，该方法将计算值与观测值之间的偏差最小化。

选择合适的次数 (n) 至关重要。当次数较低时，数据可能会出现欠拟合；而当次数非常高时，可能会捕获到噪声而不是实际趋势。数据的复杂性必须反映在多项式的次数中。一旦经过训练，模型就可以成功应用于新值的预测，并且在发生非线性关系的实际问题中，拟合更准确。

实现多项式回归

在 Python 中，我们将逐步展示如何实现多项式回归。

步骤 1：导入所需库

在此实现中，我们将导入 NumPy、Pandas、Matplotlib 和 Scikit-Learn。

步骤 2：数据加载和准备

加载数据集并显示前几行以了解数据。

输出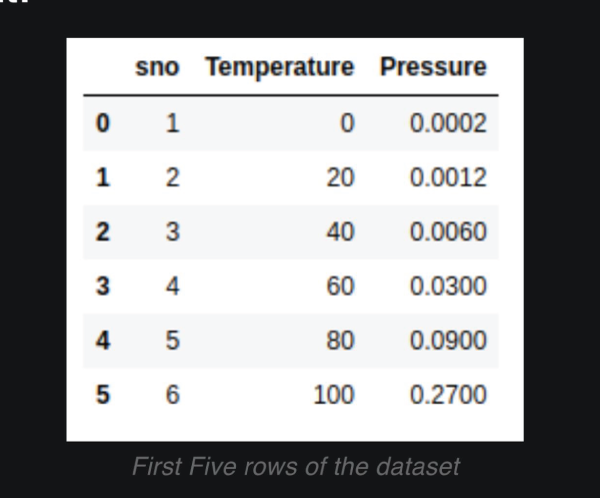

步骤 3：数据框准备

获取 X（特征）和 y（目标）。

步骤 4：拟合线性回归模型

拟合线性回归

步骤 5：多项式回归建模

将特征表示为多项式项，并给出回归模型的 4 次拟合。

步骤 6：查看线性回归结果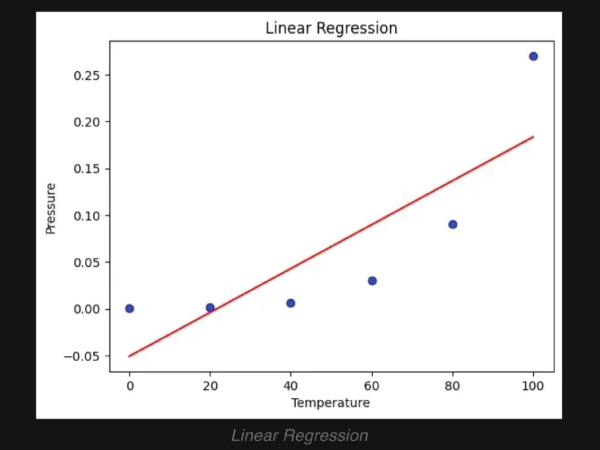

步骤 7：回归结果可视化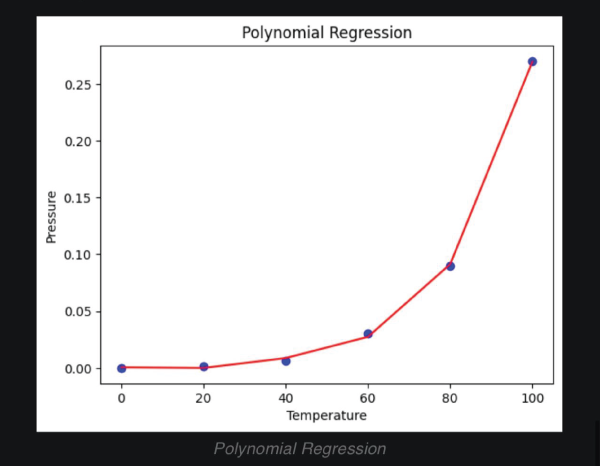

步骤 8：新结果预测

计算新值 110 的预测值

使用线性回归

输出

array([0.20675333])

使用多项式回归

输出

array([0.43295877])

示例

输出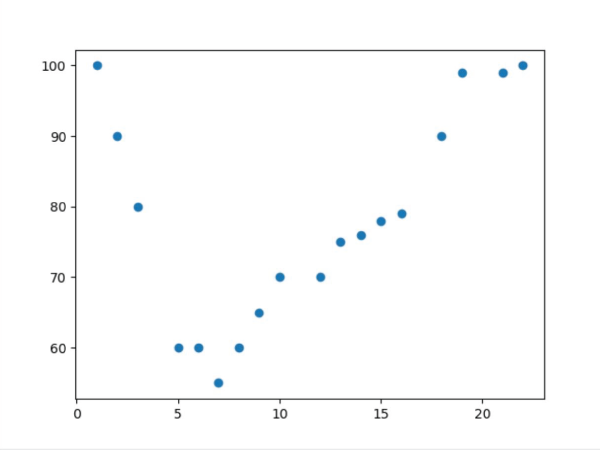

另一个示例

输出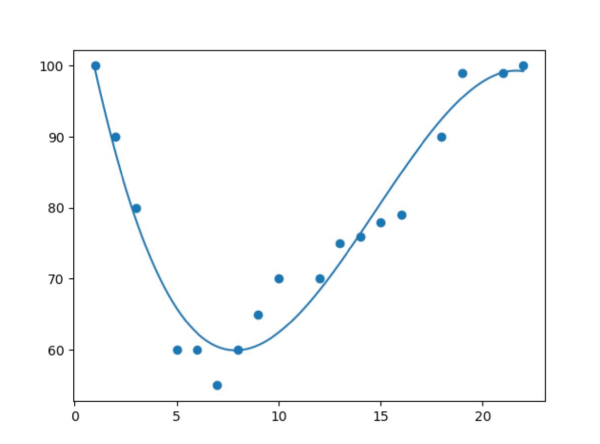

多项式回归的过拟合和欠拟合

在回归模型中，类似于神经网络的过拟合，当模型过于复杂以至于它对训练数据拟合得太好而对新数据表现不佳时，就会发生过拟合。这可以通过使用基于正则化的策略来解决，例如 Lasso 和 Ridge 回归，它们通过约束模型系数和防止冗余复杂性来发挥作用。

相反，当模型过于简单以至于无法猜测数据中的实际趋势时，就会发生欠拟合，部分原因是我们使用了低次多项式。解决方案是选择合适的多项式次数，从而使模型既不太基础也不太复杂，因此使其在先前数据和新数据上都表现良好。

偏差-方差权衡

偏差-方差权衡对于避免过拟合和欠拟合非常重要。增加多项式的次数通常会减少偏差并增强训练拟合，但这只是在一定程度上；此后，它会增加方差并导致过拟合。同样的情况也体现在训练误差和验证误差之间日益增大的差异中。任务是确定模型可以学习重要模式和对未见数据进行令人满意的泛化的最佳次数。

多项式回归的应用

多项式回归方法在那些变量关联最能描述为非线性且因此无法使用直线精确定义的领域中相当普遍。它具有以下常见应用

建模增长率

应用于非线性增长曲线，例如，不同时间的组织发育。

疾病流行病学

通过对流行病趋势的曲线效应进行非线性建模，协助监测和预测真菌病。

环境研究

应用于解释复杂模式，即湖泊沉积物中碳同位素的分布。

经济学与金融学

应用于市场非线性活动的分析，即可以通过时间预测趋势和走势。

多项式回归的优点

多项式回归的优点在于处理非严格线性数据关系，为建模提供了更大的灵活性。

拟合广泛的曲线轮廓

它能够建模各种非线性关系，因此适用于复杂数据集。

记录非线性模式

在数据具有曲线趋势而不是简单的线性回归的情况下，提供更精确的估计。

灵活建模

可以捕捉数据中的细微之处，因此适用于线性模型失效的场景。

多项式回归的缺点

尽管有多项式回归的优点，但它也有一些缺点可能会限制其应用。

对异常值的敏感性

对异常值敏感，极端值可能会扭曲结果。

过拟合

随着高次多项式的使用，始终存在构建极其复杂的模型的危险，这些模型可能非常适合训练数据集，但在另一个数据集上进行测试时，泛化能力很差。

有限的异常值检测

与线性回归相比，它识别和/或纠正异常值的自动方法较少，因此更难知道模型何时失效。

结论

多项式回归是机器学习中一种广泛应用的方法，用于捕获变量之间复杂、非线性的关系。线性回归模型的一个优点是它倾向于拟合非线性（曲线）趋势，这与简单线性回归模型中的直线模式不同。

这种灵活性使其能够在经济学、生物学和环境等领域进行更准确的预测。但是，随着多项式次数的增加，存在很大的过拟合风险，即模型可能过于紧密地拟合训练数据，但当引入新信息时却无法调整。为了优化其有效性，应平衡模型复杂性和预测性能。