L1 和 L2 正则化

正则化是回归的一种修改版本，旨在降低过拟合的风险，尤其是在数据的特征集中存在多重共线性时。特征集中高度的多重共线性会增加传统线性回归模型中系数估计的方差，导致估计对模型中的微小变化非常敏感。

通过将回归系数估计限制、减少或“正则化”到零，这种策略可以阻止我们的模型追求更复杂或更灵活的拟合，转而支持更稳定且系数方差更低的拟合。对于采用普通最小二乘法的正则线性回归模型，这是通过修改我们的标准损失函数（残差平方和，RSS）来实现的，以包含对较大系数值的惩罚。

与其他任何模型一样，正则化也有其权衡。我们必须通过调整超参数来仔细平衡偏差和方差，该超参数用于衡量额外正则化惩罚的程度。我们对数据“正则化”得越多，方差就越小，但代价是会增加更多的偏差。

L1 范数与 L2 范数

岭回归和 Lasso 回归是两种提高普通最小二乘回归对抗共线性鲁棒性的策略。这两种方法都试图最小化成本函数。成本由两项决定：残差平方和 (RSS)，它是使用传统最小二乘法计算的，以及一个额外的正则化惩罚项。在岭回归中，第二项是 L2 范数，而在 Lasso 回归中是 L1 范数。

让我们看看这些方程。在普通最小二乘法中，我们最小化以下成本函数

这被称为残差平方和 (RSS)。岭回归则求解

项是 L2 范数。

在 Lasso 回归中，我们求解

项是 L1 范数。

L2 项与 β 值的平方成正比，而 L1 范数与 β 值中的绝对值成正比。这个关键区别解释了 Lasso 回归和岭回归“工作”方式的全部差异。L1 与 L2 在机器学习的其他地方也出现过，因此理解这里发生的事情至关重要。

L1-L2 范数差异

• 鲁棒性： L1 > L2。鲁棒性指的是数据集对异常值的弹性。模型忽略数据中极端值的能力增强了其鲁棒性。L1 范数比 L2 范数更具鲁棒性，原因很明显：L2 范数将值平方，呈指数级增加异常值的成本，而 L1 范数只取绝对值，线性处理它们。
• 稳定性： L2 > L1。稳定性定义为对水平变化的抵抗力。这与鲁棒性完全相反。L2 范数比 L1 范数更稳定。随后的笔记本将探讨原因。

L1-L2 正则化器差异

• 鲁棒性： L1 > L2。鲁棒性被定义为计算难度。L2 有一个闭合形式解，因为它是一个值的平方。L1 没有闭合形式解，因为它是一个带绝对值的不可微分段函数。因此，L1 在计算上更昂贵，因为我们不能使用矩阵代数来解决它，而必须依赖近似（在 Lasso 示例中是坐标下降）。
• 稀疏性： L1 > L2。稀疏性是指具有非常重要的系数，这些系数要么非常接近零，要么非常远离零。理论上，非常接近零的系数以后可以删除。

现在我们通过实现来研究 L1 和 L2 正则化。

代码

导入库

读取数据集

EDA

我们现在将探索数据集。

输出

输出

输出

数据预处理

我们在这里选择简单而不是更复杂的程序，因为我们的重点是模型，而不是花哨的预处理方法。我们将只做足够的处理，以确保我们的回归模型可以使用并产生准确的结果。我们的步骤将包含以下内容

异常值

这里我们将删除异常值，但我们必须谨慎删除异常值，因为我们可能会丢失有用的信息，我们在图的右下角发现两个明显的异常值，它们反映了卖家“糟糕”的协议（低价换大面积）。

输出

我们选择删除这两个观测值，因为它们与其余数据不符，并且我们不希望这些明显“糟糕”的交易给我们的预测模型带来更多偏差。

数值到分类的转换

MSSubClass、OverallCond、YrSold 和 MoSold 虽然是数值型的，但它们是分类类型的特征，因此我们将在编码它们之前将它们转换为字符串。

编码分类标签

我们现在将编码所有分类特征标签，其值范围从 0 到 n_classes-1。

通过绘制目标特征的分布图，我们很快发现分布似乎呈右偏态。

输出

通常，当数据呈正态分布时，我们的回归模型效果最好。因此，为了获得最佳结果，我们将尝试使用对数变换来标准化特征。（对于右偏数据，对数变换会将分布转换为看起来更“正态”，但对于左偏数据，对数变换只会使分布更加左偏。）

输出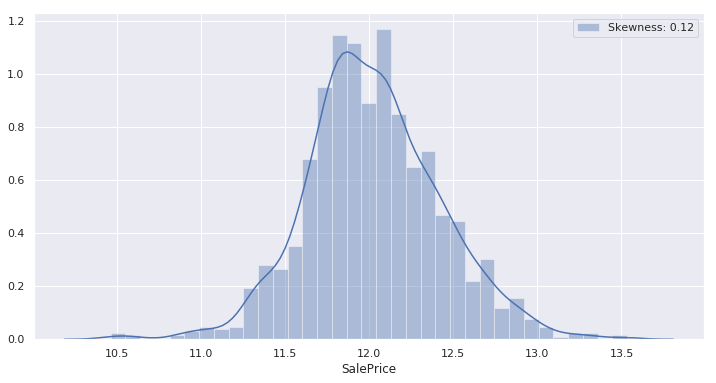

很好，我们注意到我们的对数变换表现非常好，并产生了预期的效果：新分布看起来更“正态”了。让我们将“SalePrice”的对数变换应用于我们的训练数据。

正如我们将看到的，一些非目标数值属性严重偏向右侧和左侧。这一次，我们将应用一个通用的“yeo-johnson”幂变换来尝试“规范化”它们，因为这种变换可以“规范化”右偏和左偏数据。（在这里，任何“偏度”幅度大于 0.75 的特征都被认为是“严重”偏斜的。）

输出

接下来，我们必须为所有类别特征建立虚拟/指示变量，以便它们可以在我们的回归模型中得到适当的使用。

输出

现在让我们查找缺失值并用相关特征的平均值替换它们。

输出

输出

最后，让我们设置 sklearn 所需的矩阵，然后我们可以从普通的最小二乘线性回归模型开始。这结束了我们的预处理过程。

线性回归

输出

很好，现在我们有一个数字可以与未来模型进行比较，RMSE = 0.12178。

如果我们现在拟合这个模型，我们可以检查获得的最高幅度系数的值。我们最终会将这些结果与我们的正则化模型生成的结果进行比较。

输出

我们没有观察到这里选择的任何非常高的系数，因为我们对数据进行了很好的准备。例如，如果我们没有消除异常值并标准化偏斜的数值特征，那么波动性会更大，并且模型选择一些与这些值相比明显较高的系数值的可能性会更大。即使使用这些数量，我们也会观察到正则化模型如何将它们压缩到零。

L2-正则化

L1 和 L2 正则化都旨在改进残差平方和 (RSS) 加上一个正则化项。岭回归 (L2) 的正则化项是平方系数的总和乘以一个非负比例因子 lambda（或者在我们的 sklearn 模型中是 alpha）。

为了进行比较，我们将以与典型线性回归模型相同的方式估计此模型的平均 RMSE。首先，我们将在 alpha = 0.1 的情况下执行此操作，然后我们将使用交叉验证来获得产生最低 RMSE 的最佳 alpha。值得注意的是，0.1 是随机选择的，没有特定动机。

输出

我们已经看到了对标准最小二乘线性回归模型的改进。现在，对于 alpha = 0.1 的岭回归，我们获得了 0.12046 的 RMSE。请记住，我们是随机选择 0.1 的，所以它很可能不是理想值。因此，我们有可能通过调整 alpha 来进一步提高我们的 RMSE。

让我们绘制 RMSE 随 alpha 变化的曲线，看看 alpha 值如何影响 RMSE。

输出

考虑 U 形。该图显示，最小 RMSE 发生在 alpha 值为 10-15 时。为了更精确，我们将放大 alpha 值更接近此范围的区域。

输出

输出

当 alpha = 10.62 时，RMSE 看起来很小。这似乎足以满足我们的需求，所以让我们使用这个新发现的最佳 alpha 值来计算我们修改后的 RMSE 估计。

输出

我们再次改进了 RMSE。现在，对于最佳 alpha 约为 10.62 的岭回归模型，我们获得了 RMSE = 0.11320，这比线性回归模型提高了 7.04%。这似乎是我们在不进行任何额外复杂预处理或特征工程的情况下，使用此训练数据和单个岭回归所能达到的最佳 RMSE。

在继续 Lasso 回归之前，让我们回顾一下所选系数的最大值，并将它们与线性回归模型所选的系数进行比较。

输出

正如预期的那样，与原始线性回归模型相比，正则化过程已将最大系数幅度值显著减小到接近零。

L1-正则化

输出

当使用 RMSE 进行评估时，我们可以发现 alpha = 0.1 的 Lasso 回归模型迄今为止产生的模型精度最低。在我们放弃 Lasso 回归之前，让我们应用交叉验证来微调 alpha。也许我们的 0.1 这个数字错得很离谱。

让我们尝试以与岭回归相同的方式执行此操作。

输出

最佳 alpha 看起来相当小，但我们知道它必须大于 0，所以我们将使用 sklearn 的内置 LassoCV 函数，该函数将使用交叉验证从可能的拟合选项列表中选择最佳 alpha。

注意：有一个 RidgeCV 函数，其工作方式类似，可以用于早期的 Ridge 模型。

输出

Alpha 等于 0.0004。这似乎足够接近我们的理想值，所以我们将使用这个新发现的最佳 alpha 来计算我们修订后的 RMSE 估计。

输出

很好，因此在最佳 alpha 约为 0.0004 时，Lasso 回归模型似乎在该数据集上优于最佳岭回归模型。我们现在的 RMSE 为 0.11182，比我们的线性回归模型提高了 8.17%。这似乎是我们在不进行任何更复杂预处理或特征工程的情况下，使用此训练数据和单个 Lasso 回归所能达到的最佳 RMSE。

让我们简要看一下 Lasso 回归模型认为相关的特征。请注意，Lasso 方法将为您执行特征选择——将其认为不相关的特征系数设置为零。

输出

正如预期，与原始线性回归模型选择的值相比，这些值似乎已向 0 压缩。

这是岭回归和 Lasso 回归之间需要强调的一个显著区别。岭回归惩罚高系数，但它不会通过将其系数减小到零来消除不必要的特征。它只会尝试减轻它们的影响。另一方面，Lasso 回归惩罚高系数，同时通过将不重要特征的系数设置为零来消除它们。因此，当训练具有大量不相关特征的数据集时，Lasso 模型可以帮助进行特征选择。

输出

在这种情况下，Lasso 模型似乎选择了 107 个特征，其中最相关的特征如上图所示，同时将其余 112 个特征置零。我们目前不会深入探讨具体特征，但请注意，所选特征不一定是“正确”的特征，应进行检查，尤其是在特征集中存在多重共线性时。

L0-范数

最后，为了了解 alpha 的强度如何影响所选特征的数量，绘制了由 lasso 生成的非零系数数量随正则化参数 alpha 变化而变化的图。这也被称为系数的 L0-范数。

输出

随着正则化参数 alpha 强度的增加，所选特征的数量从最大值 134 迅速下降，当 alpha 略大于 0.25 时，稳定在 4 个特征。似乎 alpha 的强度越高，lasso 模型在所选特征数量方面受到的限制就越大。在处理具有大量无用属性的数据集时，请记住这一点。