Sarimax

SARIMAX（具有外源元素的季节性自回归积分移动平均模型）是一种时间序列预测模型，它通过整合外源变量来扩展经典的SARIMA（季节性自回归积分移动平均）版本。SARIMAX主要有助于预测具有明显季节性的时间序列信息，并且可以受到外部因素的启发。

季节性是现实世界数据中常见的非平稳性的确定性来源。

现在，为了理解它，我们将通过引入SARIMA来扩展ARIMA系列时间序列模型，SARIMA是一种结合了基于季节性周期的自回归和移动平均分量来表示季节性时间序列数据的模型。我们将回顾每个参数以及它如何与其在ARIMA模型中的对应项关联。然后，我们将使用Box-Jenkins技术拟合SARIMA模型，并使用滚动预测来验证其准确性。

代码

导入库

读取数据集

输出

季节性

季节性是现实世界数据中我们必须考虑的非平稳性的普遍特征和可预测的原因。而我们的ARIMA模型只有三个因子需要处理，模拟季节性将需要四个。

这四个因子是

1. P: 季节性自回归阶数
2. D: 季节性差分阶数
3. Q: 季节性移动平均阶数
4. m: 单个季节性周期的步数。

指定为 SARIMA(p,d,q)(P,D,Q)[m]

我们将再次利用ACF/PACF图来计算季节性参数值。选择每个参数的值并非精确的练习；有一般性指导方针，并且需要进行迭代才能获得适当的模型参数。

季节性周期 (M)

我们的季节性周期 m 代表每个季节中的周期数。我们可以在 ACF 和 PACF 图中看到这一点，其中我们的值 m 对应于具有最高自相关系数的滞后。0 值始终为 1，因为它与当前时间步长有完美的关联。如果我们的数据是季节性的，我们预计与当前时间步长相关的下一个最高值将是正好一个季节之前的同一个季节点。季节性周期值也将帮助我们计算 P 和 Q。

季节性自回归阶数(P)

我们的季节性自回归阶数与我们的自回归阶数类似，不同之处在于，它不是确定影响当前时间步长值的先前时间步长的阶数，而是我们寻求 m 或季节性周期的季节阶数的先前时间步长。这就是为什么使用 m 滞后来计算 P 值。如果滞后 m 为正，则 P 应大于或等于 1。否则，P 应为零。我们可以用 1 的值拟合模型，然后根据需要进行递增。

季节性差分阶数 (D)。

我们的 D 参数的经验法则是，我们的序列和季节性差分不应超过 2。如果我们的季节性模式在整个时间段内保持恒定，我们可以设置 D=1，而设置 D=0 表示季节性模式不稳定。

季节性移动平均阶数 (Q)。

我们以与确定 P 相同的方式确定 Q。如果滞后 m 为负，则 Q >= 1，这与我们拟合 P 的方式相反。我们通常不希望 P+Q 超过 2。我们希望保持参数值最小，因为随着我们使用更复杂的模型，过拟合的风险会增加。

输出

数据探索

查看我们的时间序列，我们发现一个有趣的模式，如果没有 2007-2008 年的显著下降，这个模式可能会通过平方根变换得到纠正。这种趋势是由商业周期和其他影响经济统计数据的外源性因素引起的。为了消除趋势，我们可以使用 Box-Cox 变换。接下来，我们可以对时间序列进行差分，以解释趋势，并同时展示结果以及由此产生的 ACF 和 PACF 图。

Box-Cox 变换将非正态数据转换为正态分布。我们可以为 lambda 提供一个输入，它将自动进行对数变换、平方根变换或倒数变换。如果我们不为 lambda 提供任何参数，它将自行调整并返回一个 lambda。

输出

输出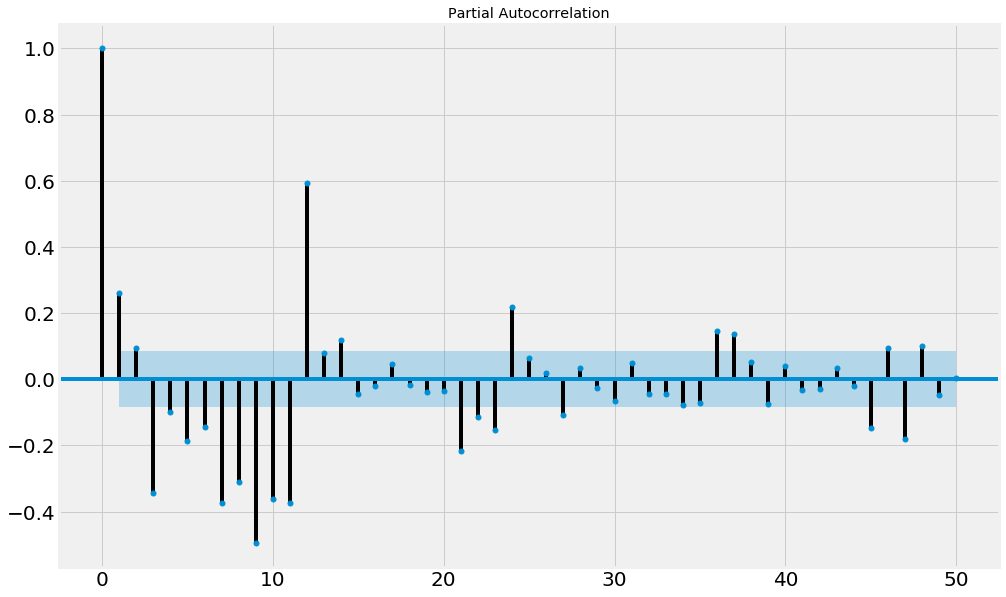

参数估计

在进行 Box-Cox 变换和差分后，我们不再有趋势，尽管季节性仍然明显且混乱。由于我们的 lambda 值接近 1（无变换），并且 Box-Cox 变换似乎没有对序列产生显著影响，我们选择将其删除，ACF 和 PACF 图显示了一个未转换的序列。我们可以使用 ACF 和 PACF 图来找到 SARIMA 模型的正确参数。

首先，查看 ACF，我们发现最大的自相关发生在滞后 12 处，这在我们原始数据和这是月度数据这一事实的背景下是合理的。

鉴于 m 为正，这意味着 P = 1 且 Q = 0。ACF 和 PACF 图均显示其第一个主要滞后为 1。所以，p = 1 且 q = 1。由于我们对序列进行了差分，d 将为 1。所以我们有以下参数：SARIMA(1,1,1)(1,0,0)[12]

我们将数据分为两组：训练集和测试集，然后拟合我们的 SARIMA 模型。

输出

模型测量

尺度相关误差

尺度相关误差是与数据尺度相同的误差。

• 均方误差 (MAE): 流行且易于理解
• 均方根误差 (RMSE)

百分比误差

百分比误差是无单位的，通常用于评估跨数据集的预测性能。百分比误差通常以 estimated_value/true_value 的形式表示。百分比错误的缺点是，当真实值为零时，它们可能导致无限或未定义的结果。此外，当数据缺乏有意义的零值时，例如温度，使用除法然后取绝对值（如 MAPE 中）可能会导致不代表真实差异的不准确结果。

• 平均绝对百分比误差 (MAPE)
• 对称 MAPE：处理 MAPE 倾向于对负误差给予更重惩罚的问题

缩放误差

缩放误差试图解决百分比误差的一些问题。

• 平均绝对缩放误差 (MASE)

输出

模型评估

不幸的是，我们的模型并不特别适合趋势。糖果预测数据的问题在于它遵循不稳定的模式。我们接下来可以做的是使用 Hodrick-Prescott 滤波器将趋势从时间序列的其余部分分离出来，该滤波器是一种旨在处理经济数据中商业周期的带通滤波器。

相反，我们将进行滚动预测。滚动预测是指我们向前预测一步，然后将模型拟合到包含测试集数据的新数据上。它成本高昂，因为必须在每个时间步长重新拟合模型，但它允许我们预见一个糟糕的步骤将如何累积到总体误差中，而不会影响未来的预测。这意味着由于趋势导致的时间序列的早期偏差不会损害我们预测未来步骤的能力。

输出

正如你现在所见，预测非常接近测试用例。因此，我们的模型表现良好。