机器学习中的粒子群优化算法

粒子群优化（PSO）是一种基于种群的优化算法，其灵感来源于鸟群或鱼群等群体的社会行为。PSO由James Kennedy和Russell Eberhart于1995年首次提出。自出现以来，它已广泛应用于机器学习领域，特别是在目标函数需要优化且复杂的情况下。与基于梯度的优化方法相比，它是一种非常有效的替代方案，尤其是在优化景观是非凸、噪声大或高维的情况下。

PSO通过模仿粒子群的运动来工作。每个粒子都代表一个优化问题的可能解。粒子在搜索空间中的移动是通过根据粒子自身的经验以及其邻居的经验信息来改变其位置来实现的。每个粒子都跟踪以下信息：

• 当前位置： 它当前代表的解决方案。
• 速度： 这是朝着更好解决方案移动的方向和大小。
• 个人最佳（pBest）： 粒子迄今为止找到的最佳解决方案。
• （gBest）全局最佳： 这是整个种群迄今为止找到的最佳解决方案。

粒子群优化算法

PSO算法侧重于通过迭代优化候选解的种群来最小化或最大化给定的目标函数。种群中的每个粒子代表一个可能的解决方案，通过改变其位置和速度在搜索空间中移动，这种移动不仅基于自身的经验，还基于其他粒子的经验。

01. 初始化

在初始化步骤中，算法在定义的搜索空间内任意为每个粒子分配一个初始位置和速度。每个粒子的初始位置对应于优化问题的某个可能解。每个粒子都维护其个人最佳位置（pBest），这是它迄今为止发现的最佳解决方案。算法还会找到全局最佳位置（gBest），即种群在给定时刻找到的最佳解决方案。

这是初始化步骤，它将使粒子开始探索搜索空间的旅程；从这里开始，后续的迭代将寻找更有希望的解决方案。

02. 更新速度

在每次迭代中，粒子速度都会更新。速度衡量每个粒子在搜索空间中穿越的速度和方向。新速度依赖于三个要素：

• 惯性： 指粒子在当前迭代中的速度，这保证了动量的保持。
• 认知成分： 个人最佳位置减去粒子当前位置之间的差值。
• 社会成分： 全局最佳位置减去粒子当前位置之间的差值。

更新速度的公式如下：

vi(t+1)= wvi(t) +c1r1(pBesti-xi(t))+c2r2(gBest-xi(t))

其中

• vi 是第 i 个粒子在迭代 t 时的速度。
• xi(t) 是粒子在迭代 t 时的位置。
• w 是惯性权重，控制粒子当前速度的影响。
• c1 和 c2 是加速度系数，分别决定了粒子倾向于其个人最佳位置和全局最佳位置的强度。
• r1 和 r2 是介于 0 和 1 之间的随机值，为粒子的行为引入了随机性。

惯性与吸引向个人最佳和全局最佳位置的吸引力之间的这种平衡，确保粒子能够有效地探索搜索空间，同时仍然收敛到有希望的区域。

03. 更新位置

计算出新速度后，粒子的当前位置按如下方式更新：xi(t+1)=xi(t) +vi(t+1)

粒子位置的这种更新使其能够在搜索空间中移动，并可能在每次迭代中找到更好的解决方案。

04. 适应度测试

在更新位置后，适应度函数决定新位置在多大程度上是优化问题的解决方案。适应度值衡量粒子与期望结果的接近程度，并随着时间的推移引导种群朝着更好的解决方案前进。

05. 更新个人最佳和全局最佳

如果获得的新位置比其 pBest 具有更好的适应度值，则粒子会用新位置更新其个人最佳。如果新位置提供了比当前 gBest 更好的解决方案，那么全局最佳也会被更新。这些更新确保种群通过向搜索空间中的更好区域移动来持续改进。

06. 终止标准

然后，算法将上述步骤迭代指定的次数，或者直到达到预定的精度水平。当满足终止条件时，算法终止并返回当前的全局最佳位置作为最优解。

PSO在机器学习中的应用

PSO在机器学习中有着大量的应用，主要是因为PSO能够很好地处理各种优化景观。以下是PSO在机器学习中应用的一些主要领域：

• 超参数优化： 为模型选择有效的超参数（例如学习率或正则化因子），如神经网络、支持向量机或决策树等机器学习模型，对模型的效率至关重要。PSO可以轻松搜索大型超参数空间以找出最佳设置。
• 使用PSO训练神经网络： PSO可以用于替换基于梯度的优化算法（如随机梯度下降）来训练神经网络。这尤其适用于梯度难以计算或损失表面高度不规则的情况。PSO不会陷入局部最小值，因此对此类任务极具吸引力。
• 特征选择： PSO可用于从大型数据库中确定最相关的特征子集，从而降低维度并提高模型性能。在此特征选择场景中，一个粒子代表一个候选特征集，适应度函数估计使用该子集训练的模型性能。
• 聚类： PSO也已用于无监督学习，例如聚类工作。它可以最小化簇内方差并优化簇中心的が位置，并且可以作为k-means等算法的替代方法。
• 强化学习： PSO在优化策略函数或动作选择策略时与强化学习相关联。当基于梯度的参数更新失败时，它在找到智能体最佳参数的过程中很有用。

为了更好地理解，我们将实现粒子群优化算法进行测试。我们将运行一些基准测试。

代码

导入库

基准测试

将使用一组从测试函数（如 Rosenbrock测试、Rastrigin测试、Ackley测试、Sphere测试、Beale测试等）开发的基准函数来处理此优化问题。我们打算在开发的基准函数上实现PSO。

以下是一些标准的基准函数，通常用于评估优化方法的性能。这些函数通常用于基准测试以评估优化算法的性能。

尽管“Rastrigin测试”曾被推荐，但我们选择了“A_Objective”函数作为我们优化过程的基准。这是应用于优化问题的两个不同的基准函数。

选择测试

我们将尝试找到由基准函数“x”、“y”和“z”表示的全局最小值和最大值点。现在，由于我们可以找到最低点和最高点并将其与其他点进行比较，因此基准测试非常容易，因为从视觉上看，我们只需查看图中更接近最小值的点。

绘制等高线图

我们想生成一个二维图，在该图中根据颜色图表示函数值。基准函数“z”将表示为图像。

它还将叠加等高线，显示函数的等高线，并在之前确定的全局最小值点处设置一个红色的“x”。

输出

上面是二维图，其中红色的“X”表示基准函数的最小值，图中的黑线表示函数的特定等高线值。该图的颜色表示将帮助您理解值的密度。

参数和初始化

现在我们将设置控制PSO算法行为和收敛的参数。

我们需要初始化PSO的粒子。

绘制点

我们将基于上面绘制的基准函数的等高线图来实现粒子群优化算法，以进行可视化。稍后，我们将在该等高线图本身上绘制点。

输出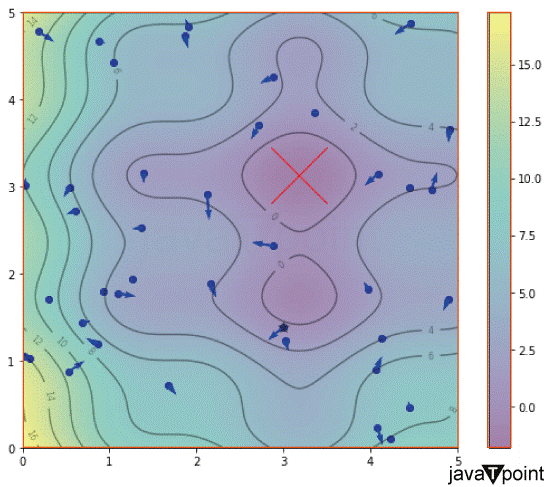

大多数粒子已经从等高线图上的最小点散开。这是第一次迭代，请在迭代后再次检查分数。

输出

PSO解决方案

• PSO在 x = 2.99421688 和 y = 1.38382531 处发现了解决方案。
• 此时，目标函数的值为 0.3668918708631955。

全局最优解

• 对于基准函数，已知的全局最优解为 x = 3.1818181818181817 和 y = 3.131313131313131。
• A_Objective 函数现在的值为 -1.8082706615747688。

生成的解决方案似乎并不精确等于全局最优解。尽管如此，PSO方法找到了一个足够接近全局最优解的解决方案。PSO的目标是找到或足够接近全局最优解，并且在某些条件下有时可能会收敛到局部最优解。重要的是要记住，影响PSO找到全局最优解成功率的因素有很多，包括超参数的选择、优化景观的复杂性以及粒子的初始化。通过调整PSO算法、调整超参数或多次运行该过程，可以提高达到全局最优解的可能性。

PSO迭代

现在，让我们直观地看看PSO迭代。

输出

因此，可以推断出粒子朝着红色的“X”或最小值移动，这在迭代过程中是可见的，从而表明该方法得到了优化，并且更接近最小值点的粒子产生了有利的优化信号。

输出

尽管不完全精确，但PSO算法收敛到一个非常接近全局最优解的值。在此方面，尽管粒子群优化算法的目标是在搜索空间内找到全局最优解，但在某些情况下它可能会收敛到局部最优解。通过PSO进行的优化在每次迭代中都在改进。