线性回归与自回归模型之间的区别2025年6月18日 | 阅读 12 分钟 线性回归和自回归模型是预测建模中最常用的统计工具。尽管它们在分析数据时应用数学关系的做法很相似,但它们的目的、结构和应用却有显著差异。因此,为了选择适合任何问题的模型,需要理解这些差异。 线性回归线性回归是一种预测建模技术,它考虑因变量与一个或多个自变量之间的关系,旨在找到一个最佳预测因变量的线性方程。线性回归模型的一般形式是:Y=β0 +β1X1 +β2X2 +⋯+βnXn +ϵ,其中Y是因变量,Xi是自变量,βi表示系数,ϵ是误差项。模型需要满足以下假设:因变量与自变量之间应存在线性关系,同方差性,即误差方差应恒定,观测值应独立,并且误差必须服从正态分布。 自回归模型自回归(AR)模型是一种时间序列模型,它利用所有过去的值来预测未来值,并假定与过去观测值存在线性依赖关系。AR模型的一般形式是 Yt =ϕ1Yt−1 +ϕ2Yt−2 +⋯+ϕpYt−p +ϵt,其中Yt代表当前值,Yt−i是滞后值,ϕi是系数,ϵt是误差项。该模型在特定假设下成立,其中时间序列的平稳性意味着均值和方差随时间恒定,并且误差项是白噪声,表明它们同分布且均值为零且独立。 以下是线性回归和自回归模型之间的一些主要区别。
现在,为了更好地理解它们的用例,我们将使用线性回归模型。 导入库加载数据输出  变量信息
输出  从这里可以看到,数据中个人的平均年龄是39岁。年龄值的标准差为14。这意味着平均而言,典型的年龄分布在25至64岁之间。我们可以发现数据的最大值和最小值点,以了解其中是否存在异常值。 根据BMI分数,此数据集中有很多肥胖和超重的人。总的来说,数据集中的大多数人都至少有一个孩子。 输出  我们来看看缺失值。 在实施机器学习的过程中,数据集中的缺失数据可能会导致不正确的结果。因此,我们应该找出并纠正数据集中的缺失信息。 输出 输出  上面显示的数据集非常好。我们的数据集不包含任何缺失信息。 不一致性观察现在我们将查找不一致性。虽然机器学习模型的百分比构成是95%的预处理和5%的模型选择。我们需要用正确的数据知识来训练模型。需要使用特定的预处理技术来准备可用于机器学习的数据。异常值分析是其中一项技术。数据集中的任何数据点,其值与其他观测值显著不同,都称为异常值。换句话说,它是与整体模式显著不同的观测值。  由于异常值与数据模型行为不同,并且会增加过拟合的错误,因此有必要识别异常值模型并对其进行一些调整。可以使用各种可视化技术来查看矛盾的观测值。其中之一是箱形图。其他群体被聚集在一起并显示在框中,而异常值则被显示为点。 输出  输出     从上面的图表中可以看出,费用和BMI读数的值存在异常值。不过,这些并没有影响我们的数据集。相反,这些数据使我们更容易对数据进行评论。因此,我们不会以任何方式处理这些数据。 模型现在我们将构建我们的线性回归模型。 输出 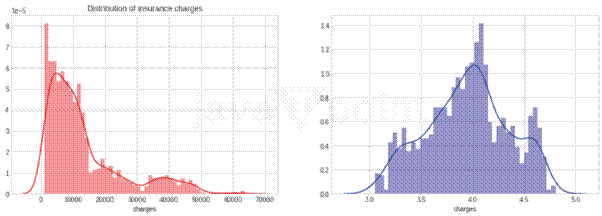 输出  输出  输出  输出 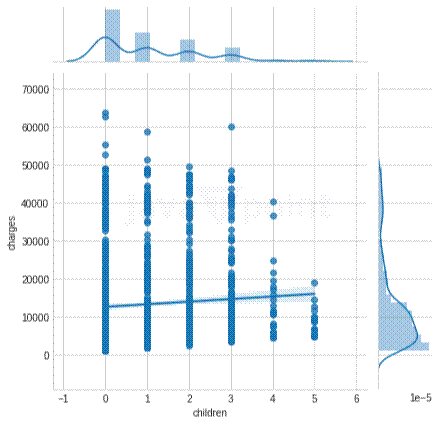 输出  实际上,当自变量多重共线性时,就会出现一种称为“虚拟变量陷阱”的情况。也就是说,两个或多个变量高度相关,但可以通过一个变量预测另一个变量。 通过使用pandas的get_dummies函数,可以一行代码完成上述所有步骤。为了将sex、children、smokers和region特征编码为虚拟变量,我们将使用此函数。当设置drop_first=True时,删除一个变量和原始变量将消除虚拟变量陷阱。pandas使我们的工作更加轻松。 输出  标准化有两个主要目的:提高数据的一致性或准确性,以及消除数据库中的冗余数据。 标准化适用于各级数据库,以及范式。为了使数据库适合任何一种范式,它必须满足相关范式的每个要求。 标准化执行得当可以极大地提高数据库的速度。 输出  输出  输出  输出 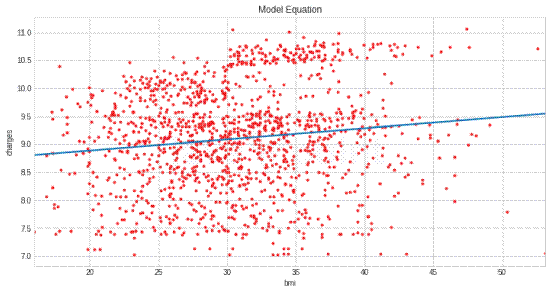 输出  现在,是时候看看自回归模型的用例了。 导入库 我们将验证目录的结构并确保所有预期文件都存在。 输出  现在,我们将使用80-20的比例将文件列表分割成训练集和测试集。 输出  以下函数使用一些基本的数据清理转换和可视化任务来预处理传感器数据文件。首先,它记录正在处理的文件类型和索引,以及文件名和初始列名。该函数将CSV文件读入Pandas DataFrame,并删除任何包含缺失值的行。它将第一列重命名为“Sensor Value”,并进行迭代检查该列中的非数字条目,记录并删除任何无效行。传感器值转换为浮点类型,以便进行数值运算。该函数提供DataFrame的摘要描述,包括其形状、列名和数据类型。就可视化而言,它创建了一个折线图以查看数据趋势,一个滞后图以查看数据是否自相关,以及一个自相关图以了解不同滞后的相关性。最后一点是经过清理和处理的DataFrame,用于进一步分析,然后为数值或机器学习任务做好准备。 CreateTrainTestData函数根据指定的断点将数据集分割成训练集和测试集。该函数分割输入数据,将断点之前的所有元素放入训练集,并将所有剩余元素包含在测试集中。 initializeRunModel函数使用提供的训练数据来初始化、训练和诊断AR模型。它首先使用提供的训练数据集初始化AR模型,然后拟合模型进行训练。训练后,该函数检索并打印出选择的滞后值k_ar和模型参数params,它们是AR模型的重要组成部分。 predict函数旨在利用已训练的AR模型对测试数据集进行预测。它首先使用模型对测试数据范围进行预测,该范围从训练数据之后开始,一直持续到测试数据集的末尾。 现在,我们有了一个可以处理测试和预测数据的函数。 然后,我们将加载单独的文件,然后形成组合数据。 输出     rolling_Autoregression函数实现了基于自回归时间序列模型的滚动或前向验证过程。它首先根据提供的断点将给定数据集分割成训练集和测试集。然后,它初始化一个包含先前观测值的历史列表和一个空的预测列表,用于存储模型的预测。 输出   rolling_ARIMA函数是一种时间序列预测方法,它使用前向验证和ARIMA滚动。它首先根据提供的断点将数据分割成训练集和测试集。然后,它创建了一个空的预测列表,以便其中可以包含模型的输出。 输出   现在我们将使用OhioT1DM数据集,因此我们将加载并预处理它。 输出    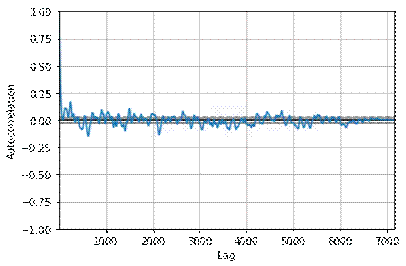 输出   输出   下一个主题机器学习中的精确率和召回率 |
我们请求您订阅我们的新闻通讯以获取最新更新。