置信区间

统计推断是通过分析样本数据来获得对数据来源总体的洞察，以及分析数据样本之间的变异性。在数据分析中，我们经常对大总体的特征感兴趣，但收集关于整个总体的所有数据可能不切实际。例如，在美国总统选举之前，了解每一位合格选民的政治倾向将非常有益，但普查每一位选民并不现实。取而代之的是，我们可以调查总体的子集，例如 1000 名已注册选民，并利用结果来推断整个总体。

点估计

点估计是从抽样数据中推导出的总体参数的估计值。例如，如果我们想确定美国注册选民的平均年龄，我们可以对注册选民进行民意调查，然后使用受访者的平均年龄来估计整个总体的平均年龄。样本均值是指样本的平均值。

样本均值通常不等于总体均值。这种差距可以归因于多种原因，包括不充分的调查设计、有偏见的抽样程序以及从总体中选择样本的内在不可预测性。让我们通过创建一个随机年龄数据总体，然后从中选择一个样本来估计均值，以此来考察点估计。

输出

输出

我们基于 500 人的样本的点估计值比真实的总体均值偏离 0.6 岁，但还是比较接近。这说明了一个重要的观点：通过对一小部分人进行抽样，我们可以相当准确地估计一个庞大的总体。

另一个可能有用的点估计是属于特定类别或子群体的人口百分比。例如，我们可能想知道我们调查的每位选民的种族，以便对选民群体的整体人口统计特征有所了解。您可以通过抽取一个样本，然后计算样本中的比例来获得此类百分比的点估计。

输出

请注意，比例估计值与真实的潜在总体比例有多接近。

抽样分布与中心极限定理

许多统计过程都假设数据遵循正态分布，正态分布具有对称性等理想特性，大部分数据都聚集在均值几个标准差的范围内。不幸的是，现实世界的数据很少是正态分布的，样本的分布通常反映了总体的分布。这意味着从具有偏斜分布的总体中抽取的样本也很可能被偏斜。让我们通过可视化我们之前准备的数据和样本来评估偏斜度。

输出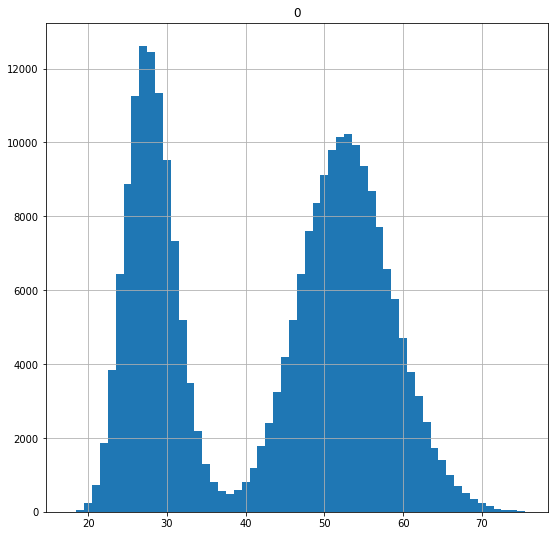

该分布具有中度偏斜，但图形清楚地表明数据不是正态的：它不是一个单一的对称钟形曲线，而是具有双峰分布，有两个高密度峰值。我们从该总体中抽取的样本应该具有几乎相同的形状和偏斜度。

输出

样本的形状与潜在总体大致相同。这意味着我们不能将基于正态分布的方法应用于此数据集，因为它不是正态的。事实上，根据中心极限定理，我们可以这么做。

中心极限定理是概率论中最基本的定理之一，它构成了许多统计分析方法的基础。总的来说，该定理断言，许多样本均值的分布（通常称为抽样分布）将呈正态分布。即使底层分布不是正态分布，此标准也适用。因此，我们可以将样本均值视为来自正态分布。

为了演示，让我们通过从我们的总体中获取 200 个样本，然后创建 200 个均值的点估计来构建一个抽样分布。

输出

尽管样本是从双峰总体分布中抽取的，但抽样分布看起来几乎是正态的。此外，抽样分布的均值接近真实的总体均值。

输出

我们抽取的样本越多，我们估计总体参数的可能性就越大。

置信区间

点估计可以提供对均值等总体参数的近似估计，但估计值容易出错，并且为了获得更优的估计而获取更多样本可能不切实际。置信区间是一组围绕点估计的数字，它以一定的置信水平反映了真实的总体参数。例如，如果您希望使用点估计及其匹配的置信区间以 95% 的概率捕获真实的总体参数，您将置信水平设置为 95%。更高的置信水平会导致更宽的置信区间。

要计算置信区间，请从点估计开始，然后加上和减去一个误差范围以获得一个范围。误差范围取决于您选择的置信水平、数据分布和样本大小。计算误差范围的方法取决于您是否知道总体的标准差。

如果您知道总体的标准差，误差范围等于

其中 σ (sigma) 是总体标准差，n 是样本大小，z 是 z 临界值。z 临界值是从正态分布均值开始计算的，它包含了与所选置信水平相关联的数据比例。例如，我们知道在正态分布中，大约 95% 的数据落在均值 2 个标准差范围内，因此我们可以选择 2 作为 95% 置信区间的 z 临界值。

让我们为我们的均值点估计计算一个 95% 的置信区间。

输出

我们估计的置信区间对应于真实的总体均值 43.0023。

为了更深入地理解“捕获”真实均值意味着什么，让我们构建并可视化多个置信区间。

输出

如果您查看上图，您会发现除了一个之外，所有的 95% 置信区间都与代表真实均值的红线重叠。这符合预期，因为 95% 的置信区间在 95% 的情况下会捕获真实均值。

如果您不知道总体的标准差，您必须使用样本的标准差来计算置信区间。当总体标准差未知时，区间会更容易出错。为了解决这个问题，我们使用 t 临界值而不是 z 临界值。t 临界值是使用 t 分布计算的，t 分布类似于正态分布，但随着样本量的减小而变得越来越宽。t 分布在 scipy.stats 中以“t”别名提供，允许我们使用 stats.t.ppf() 获取 t 临界值。

让我们抽取一个较小的样本，然后使用 t 分布在不知道总体标准差的情况下构建一个置信区间。

输出

请注意，t 临界值大于我们为 95% 置信区间选择的 z 临界值。这使得置信区间能够更广泛地覆盖，以弥补使用样本标准差而非总体标准差所引入的不可预测性。最终结果是置信区间显著变宽（误差范围更大）。

注意：使用 t 分布时，您必须提供自由度 (df)。对于此类测试，自由度是样本大小减一。当样本量很大时，t 分布会趋近于正态分布。

如果您有一个大样本，t 临界值将接近 z 临界值，因此使用正态分布和 t 分布之间的差异很小。

输出

与其手动生成均值点估计的置信区间，不如使用 Python 函数 stats.t.interval()。

输出

我们还可以计算总体比例点估计的置信区间。在此示例中，误差范围是

其中 z 是我们置信水平的 z 临界值，p 是总体比例的点估计，n 是样本大小。让我们使用先前估计的样本比例 (0.192) 为西班牙裔创建 95% 的置信区间。

输出

结果表明，置信区间捕获了真实的总体参数 0.2。与对总体均值点估计所做的一样，我们可以使用 scipy stats.distribution.interval() 函数来创建总体比例的置信区间。在此示例中，我们处理的是 z 临界值，因此我们希望使用正态分布而不是 t 分布。

输出

我们可以指出，通过抽样估计总体参数是一种基本而有效的推断方法。