机器学习中的矩阵分解

矩阵分解是数学应用于机器学习的最强大工具之一，用于将复杂的数据结构分解为易于处理的形式。在这方面，如果机器学习从业者能适当理解和应用矩阵分解技术，它们对于提高模型性能、计算效率以及洞察底层数据是不可或缺的。

矩阵分解简单来说就是将一个矩阵分解成若干个成分矩阵，这些成分矩阵相乘后可以重构出原始矩阵。这能轻易地简化许多数学运算，并应用于数据分析、降维或优化等多个领域。

基本上，矩阵分解旨在以某种形式表示矩阵，从而显式地揭示矩阵的内在属性，进而简化计算并提取有意义的模式。同时，有多种分解技术可供选择，用于不同类型的矩阵和应用，因此提供了灵活性和通用性。

矩阵分解的类型

现在，我们将介绍机器学习中几种关键的矩阵分解类型。

1. 奇异值分解（SVD）：在众多矩阵分解方法中，奇异值分解（SVD）是最重要的方法之一。通过这个过程，一个给定的矩阵被分解成三个基本矩阵，这三个矩阵共同提供了一种分析和操作原始矩阵特性的途径。SVD 在降维过程中非常有用，有助于将数据集简化为其最重要的特征，并丢弃噪声或无关信息。它常用于主成分分析（PCA）中，将数据投影到低维空间，同时保留最大方差。此外，SVD 还应用于推荐系统，通过分解用户和物品之间的交互矩阵来识别决定偏好的潜在因素。SVD 的通用性很强，可以处理任何矩阵，这使得它在机器学习、图像处理和信号处理等许多领域都非常方便。
2. 特征值分解：特征值分解，也称为谱分解，是一种应用于方阵的方法。特征值分解将一个矩阵分解为特征向量和特征值，这对于了解线性变换的属性非常重要。这种分解使我们能够推断出那些以线性方程为模型的系统的行为。在机器学习中，特征值分解是主成分分析的核心，该分析旨在寻找数据中方差最大的方向。通过分析协方差矩阵，这项技术是降维和特征提取的核心。它在稳定性分析、振动分析以及求解线性方程组中也扮演着重要角色，其中特征值提供了关于系统行为的非常重要的信息。尽管这种方法很有效，但它要求矩阵是方的且可对角化，因此其适用性可能比其他分解技术有限。
3. LU 分解：LU 分解是一种矩阵分解技术，其中一个矩阵被表示为一个下三角矩阵和一个上三角矩阵的乘积。这种分解在求解线性方程组、矩阵求逆、计算行列式以及其他一些相关运算中非常有用。由于其计算效率高和实现简单，数值分析中优先使用 LU 分解，特别是对于大型矩阵。它将一个矩阵表示为更简单的上三角和下三角形式的乘积，从而将复杂的操作分解为可管理的任务来解决线性系统。LU 分解用于高斯消元法，并通过分解系数矩阵来简化方程的求解。此外，求解大型线性系统的迭代方法也使用它。因此，它是科学计算和工程应用的重要工具之一。但是，它要求矩阵是方的且非奇异，在某些情况下，可能需要采用主元选择策略来处理数值不稳定性。
4. QR 分解：QR 分解是将一个矩阵分解为一个正交矩阵和一个上三角矩阵的乘积的方法。它在解决线性系统、特征值问题和最小二乘法拟合中有广泛应用。正交矩阵包含单位向量，确保了各种计算中的数值稳定性。特别是在数值方法中，QR 分解非常有用，因为它可以帮助在不直接求逆矩阵的情况下进行运算，从而增加了操作的稳定性和效率。它在通过格拉姆-施密特过程正交化向量以及回归分析中的优化算法中都有应用。其正交性保证了计算的稳定性；因此，QR 分解对于要求精度的应用来说是可靠的。处理非方阵的能力以及该方法的数值稳定性，使其在理论和实践领域都非常通用。
5. Cholesky 分解：Cholesky 分解是专为正定矩阵设计的一种特殊方法。它将一个矩阵分解为一个下三角矩阵及其转置的乘积，为求解线性方程组和矩阵求逆提供了一种简化的方法。特别地，这种分解在优化问题中非常方便，能同时提高计算效率和数值稳定性。Cholesky 分解的主要应用在于机器学习，特别是在包含协方差矩阵的模型中，如高斯过程和卡尔曼滤波器。它通过促进矩阵逆和行列式的快速计算，在概率建模和数据分析中扮演着关键角色。下三角矩阵中的元素是原始矩阵元素的平方根。这确保了计算的高效性和稳定性。尽管对于正定矩阵非常有用，但这种分解不适用于非正定矩阵的场景；因此，其应用仅限于特定情况。
6. 非负矩阵分解（NMF）：非负矩阵分解是一种矩阵分解技术，它将一个输入矩阵分解为两个非负矩阵。它特别适用于由非负值组成的数据，例如图像、文本和音频数据。NMF 的应用包括聚类和主题建模，它可以发现数据中的潜在结构和模式。强加的非负性约束确保了分解出的成分保持可理解性；因此，它推动了 NMF 在许多需要人类理解的现实世界应用中的普及。在主题建模中，NMF 用于识别文档的主题。在这里，每个文档被表示为潜在主题的线性组合。由于该算法能够在没有任何正交性约束的情况下发现有意义的模式，它能找到可解释的、基于部分的表示。因此，NMF 成为从图像处理到生物信息学等广泛领域中一种相当通用的工具。

代码

现在，我们将构建一个模型，用于将新闻文章分为不同的类别，我们将使用矩阵分解作为主要技术。

导入库

读取数据集

EDA（探索性数据分析）

现在，让我们来看一下比赛提供的数据集。根据经验，在进行任何模型构建或模型训练之前，最好先查看一下你正在处理的数据。通常建议在进行任何探索性数据分析（EDA）之前，先将数据分成训练集和测试集，因为作为研究人员，你不希望因结果而产生偏见，这可能导致过拟合。因此，我们不会查看或试验所提供的测试数据，仅将其用于测试模型。

输出

我们需要创建一个包含已分类文章、文章ID（ArticleID）及其所属类别的数据框（dataframe）。我们还发现，每个文章ID都是唯一的，而类别则会重复出现。既然我们知道了最终目标的数据结构，那就让我们继续处理训练数据本身。

我们可以在下面的数据框中看到，我们有三列，分别是：

ArticleID：标识文章的唯一编号。

Test：文章标题和文本。

Category：用户分配给文章的类别。

输出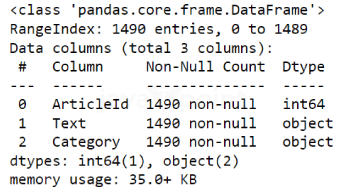

所有这些信息都如预期般呈现。我们有两个对象类型的列和一个整数类型的列（用于ID）。似乎没有缺失的行。由于我们处理的是文本数据，因此无法真正确定像 9999 或 0 这样的值是否是缺失值。在继续之前，让我验证一下数据中没有重复的文章。通过以下代码，我们能够知道我们有 1490 个唯一的 ID。此外，回想一下数据框将有 1490 行的事实，因为我们可以假定一篇文章是唯一的，我们可以继续形成一些令人放心的假设。我还检查了有多少个类别值。我们可以在下面看到有五个值：business（商业）、tech（科技）、politics（政治）、sport（体育）和 entertainment（娱乐）。

输出

输出

我们首先想看的是几段文本，以了解它们在数据框中是如何保存的。为此，我们将查看第一行。我们可以看到文本以标题开头，然后是相当数量的文本，这应该是文章的正文。我们可以判断它已经经过某种程度的预处理，因为没有大写字符。我们也可以假设不会有拼写错误。大小写和拼写是自然语言处理中两个比较重要的元素。我们很庆幸数据已经以这种方式被处理过了。

输出

现在，在运行一些模型之前，让我们尽可能地将数据可视化。我们可以看到，总的来说，每个类别的条目数量大致相等。这很好，因为如果一个或两个类别在数据中严重不足或过多，可能会导致我们的模型产生偏见，和/或在部分或全部测试数据上表现不佳。

输出

现在，在文本数据处理中，需要使文本对计算机“可读”。我们通过移除标点符号来做到这一点。

移除停用词——常见的英语单词，如 'to', 'the', 'of' 等。

输出

此外，在清理了数据框的文本单元格之后，我们还将对文本进行分词和词形还原。分词意味着将一串单词分割成一个单词列表。例如，“He is a boy” 会被转换为 ['He', 'is', 'a', 'boy']。在分词中，每个词都被切分开，以便之后在训练模型时更容易使用。之后我们将对文本进行词形还原。可以选择词形还原或词干提取。对于这个项目，我选择了词形还原，因为它比词干提取保留了更多的信息。词形还原的一个例子是，将 'running', 'horses', 和 'adjustable' 这些词，还原为 'run', 'horse', 和 'adjust'。这保留了词语的大致含义，但能让模型更好地学习。此外，我们还要确保所有单词都是小写的。

下面是清理后我们看到的结果：每篇文章的词数。大多数文章大约有 200 个词。然而，如图所示，我们也有一些严重的异常值，达到了 750 多个词！实际上，我们将移除这些异常值，因为它们可能会在之后影响我们的模型，此外还会产生更多的特征或单词，需要在模型中进行计算。

输出

输出

下面是每个类别词数的箱形图。在每个类别内部，我们也看到相当多的异常值，这次我们将保留它们。我们还看到，每个类别的平均词数相似，其中“科技”和“政治”类别的词数和方差比其他主题要多。

输出

模型

在这里，我们将构建并训练我们的模型。

对于这个使用矩阵分解的模型，我发现以上是获得最高准确率的最佳参数组合。我还通过更改 TfidfVectorizer 和/或 NMF 模型的参数尝试了其他组合。特别地，我在 TfidfVectorizer 中调整了 min_df 和 max_df。

使用了 0.85、0.90、0.95 的 max_df 值。

这些分别使用了 0、1 和 2 的 min_df 值。

它使用 'frobenius' 和 'kullback-leibler' 作为 beta_loss。

它使用 'mu' 和 'cd' 作为求解器。

输出

输出

模型比较

我们被要求使用无监督学习，通过矩阵分解模型对文本文章进行分类。传统上，如果我们有预先标记的文本（我们确实有），监督模型在这种类型的数据上会表现得更好。因此，我们将把上面的无监督学习模型与下面的监督模型进行比较。由于没有指明要使用哪种监督模型，为了方便起见，让我们创建一个 KMeans 聚类模型。为了保险起见，让我们再次导入数据，因为我们将使用另一个新模型。

输出

现在，让我们在测试集上测试这个模型。同样，所有之前在训练集上做过的数据清理步骤，都需要在这里重复一遍。

看来我们的训练准确率达到了 93.69%，但测试准确率只有 62.99%。这似乎强烈表明我们的模型对训练数据过拟合，在对新数据进行预测时表现极差。如果我们想训练一个更强大的监督学习模型，可以使用集成方法和/或 K 折交叉验证技术，或者使用不同的模型，如决策树、随机森林、支持向量机等。然而，由于本课程专注于无监督学习技术，并且这是本项目的主要焦点，所以我们将停止对我们的 KMeans 模型与矩阵分解模型的比较。