支持向量机算法

支持向量机（SVM）是最受欢迎的监督学习算法之一，用于分类和回归问题。然而，主要用于机器学习中的分类问题。

SVM算法的目标是创建一个最佳的直线或决策边界，将n维空间分割成不同的类别，以便将来可以轻松地将新的数据点放入正确的类别中。这个最佳决策边界被称为超平面。

SVM选择有助于创建超平面的极端点/向量。这些极端情况被称为支持向量，因此算法被命名为支持向量机。下面是使用决策边界或超平面对两个不同类别进行分类的图示。

示例：可以使用我们在KNN分类器中使用的示例来理解SVM。假设我们看到一只奇怪的猫，它也有一些狗的特征，所以如果我们想要一个能够准确识别它是猫还是狗的模型，那么可以使用SVM算法创建这样的模型。我们将首先用大量的猫狗图片训练我们的模型，以便它可以学习猫狗的不同特征，然后我们用这个奇怪的生物来测试它。因此，当支持向量在猫狗这两个数据之间创建决策边界并选择极端情况（支持向量）时，它会看到猫和狗的极端情况。基于支持向量，它会将其分类为猫。考虑下面的图示。

SVM算法可用于人脸检测、图像分类、文本分类等。

SVM 的类型

SVM可以有两种类型：

• 线性SVM：线性SVM用于线性可分数据，这意味着如果一个数据集可以使用一条直线将其分为两类，那么这样的数据被称为线性可分数据，使用的分类器称为线性SVM分类器。
• 非线性SVM：非线性SVM用于非线性可分数据，这意味着如果一个数据集不能用直线来分类，那么这样的数据被称为非线性数据，使用的分类器称为非线性SVM分类器。

SVM算法中的超平面和支持向量

超平面：在n维空间中，可能存在多条直线/决策边界来分隔不同的类别，但我们需要找到有助于分类数据点的最佳决策边界。这个最佳边界被称为SVM的超平面。

超平面的维度取决于数据集中存在的特征。也就是说，如果有2个特征（如图所示），那么超平面将是一条直线。如果有3个特征，那么超平面将是一个二维平面。

我们总是创建一个具有最大间隔的超平面，这意味着数据点之间的最大距离。

支持向量

最接近超平面并影响超平面位置的数据点或向量被称为支持向量。由于这些向量支持超平面，因此被称为支持向量。

SVM是如何工作的？

线性SVM

可以使用一个示例来理解SVM算法的工作原理。假设我们有一个包含两种标签（绿色和蓝色）的数据集，并且数据集有两个特征x1和x2。我们想要一个分类器，可以将坐标对(x1, x2)分类为绿色或蓝色。考虑下面的图像。

因此，由于这是2D空间，我们可以很容易地用一条直线分离这两个类。但是，可以有多个直线来分离这些类。考虑下面的图像。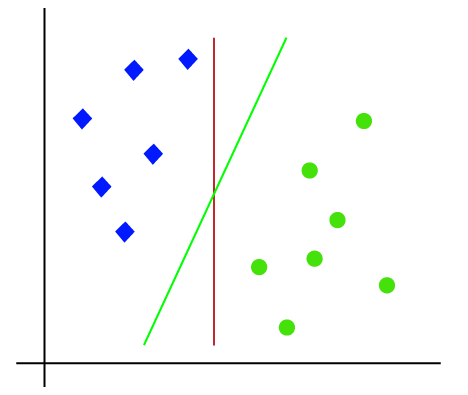

因此，SVM算法有助于找到最佳直线或决策边界；这个最佳边界或区域被称为超平面。SVM算法找到来自两个类别的最近点。这些点称为支持向量。向量与超平面之间的距离称为间隔。SVM的目标是最大化这个间隔。具有最大间隔的超平面称为最优超平面。

非线性SVM

如果数据是线性排列的，我们可以用直线来分离它，但是对于非线性数据，我们无法画出一条直线。考虑下面的图像。

因此，为了分离这些数据点，我们需要添加一个额外的维度。对于线性数据，我们使用了两个维度x和y，所以对于非线性数据，我们将添加第三个维度z。它可以计算为：

z=x2 +y2

通过添加第三个维度，样本空间将变成如下图像。

那么，SVM将按以下方式将数据集分成不同的类别。考虑下面的图像。

由于我们在3D空间中，因此它看起来像一个平行于x轴的平面。如果我们将其转换为2D空间，z=1，那么它将变成：

因此，在非线性数据的情况下，我们得到半径为1的圆周。

Python实现支持向量机

现在我们将使用Python实现SVM算法。在这里，我们将使用与逻辑回归和KNN分类中使用的相同数据集user_data。

• 数据预处理步骤

直到数据预处理步骤，代码将保持不变。以下是代码：

执行上述代码后，我们将预处理数据。代码将提供数据集：

测试集的缩放输出将是：

将SVM分类器拟合到训练集

现在，训练集将被拟合到SVM分类器。为了创建SVM分类器，我们将从Sklearn.svm库导入SVC类。以下是代码：

在上面的代码中，我们使用了kernel='linear'，因为我们在这里为线性可分数据创建SVM。但是，我们可以更改它以用于非线性数据。然后我们将分类器拟合到训练数据集(x_train, y_train)。

输出

Out[8]: 
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='linear', max_iter=-1, probability=False, random_state=0,
    shrinking=True, tol=0.001, verbose=False)

可以通过更改C（正则化因子）、gamma和kernel的值来改变模型的性能。

• 预测测试集结果
  现在，我们将预测测试集的结果。为此，我们将创建一个新的向量y_pred。以下是代码：

在获得y_pred向量后，我们可以比较y_pred和y_test的结果，以检查实际值和预测值之间的差异。

输出：以下是测试集预测的输出。

• 创建混淆矩阵
  现在我们将查看SVM分类器的性能，与逻辑回归分类器相比，有多少不正确的预测。为了创建混淆矩阵，我们需要导入sklearn库的confusion_matrix函数。导入函数后，我们将使用一个新变量cm调用它。该函数主要接受两个参数：y_true（实际值）和y_pred（分类器返回的目标值）。以下是代码：

输出

从上面的输出图像可以看出，有66+24=90个正确预测，8+2=10个错误预测。因此，我们可以说我们的SVM模型比逻辑回归模型有所改进。

• 可视化训练集结果
  现在我们将可视化训练集结果，以下是代码：

输出

通过执行上述代码，我们将获得以下输出：

正如我们所见，上面的输出与逻辑回归的输出相似。在输出中，我们得到了直线作为超平面，因为我们在分类器中使用了线性核。并且我们已经在上面讨论过，对于2D空间，SVM中的超平面是一条直线。

• 可视化测试集结果

输出

通过执行上述代码，我们将获得以下输出：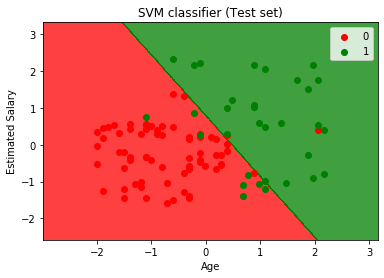

从上面的输出图像中可以看出，SVM分类器已将用户分为两个区域（已购买或未购买）。购买SUV的用户在红色区域，带有红色散点图。未购买SUV的用户在绿色区域，带有绿色散点图。超平面已将两个类别划分到“已购买”和“未购买”变量中。

关于支持向量机算法的选择题练习

1.支持向量机（SVM）算法的关键思想是什么？

1. 最大化决策边界与最近数据点之间的间隔。
2. 最小化决策边界与最近数据点之间的间隔。
3. 最大化支持向量的数量。
4. 最小化支持向量的数量。

2.在SVM中，以下哪种核函数常用于非线性分类？

1. 线性核。
2. 多项式核。
3. 径向基函数（RBF）核。
4. Sigmoid核。

3.SVM算法如何处理数据集中的异常值？

1. 它在训练期间忽略异常值。
2. 它在训练期间给予异常值更高的权重。
3. 它将异常值视为支持向量。
4. 它调整决策边界以适应异常值。

4.在SVM中，正则化参数C的目的是什么？

1. 控制决策边界的平滑度。
2. 控制间隔的宽度。
3. 处理数据集中类别不平衡的问题。
4. 控制最大化间隔和最小化分类错误之间的权衡。

5.关于SVM，以下哪个陈述是正确的？

1. SVM仅适用于二元分类。
2. SVM是参数化算法。
3. SVM对特征缩放敏感。
4. SVM是概率分类器。