极限和连续性简介2025年6月20日 | 阅读 4 分钟 机器学习 (ML) 领域关注于操纵复杂的数学函数,将输入映射到输出。对一些数学概念(如极限和连续性)有一个基本层面的理解对于开发稳健的建模技术非常重要。这些概念对于优化、损失函数和反向传播尤为重要。 极限描述了当自变量值接近某个特定值时函数的行为。极限对于导数、梯度和优化技术的定义很重要。 极限分析是机器学习应用的核心。在计算梯度时,极限对于定义导数至关重要,用于梯度下降等基于梯度的优化算法的训练。关于损失函数的分析,了解这些函数在最优点附近的行为有助于在训练过程中实现更好的收敛性和稳定性。此外,极限提供了关于激活函数在极端值处如何行为的见解,确保通过神经网络的输入数据转换是平滑的。 代码 输出 Approximate limit at x=1: 2.0 连续性意味着函数将表现出平滑的行为,其图表中没有任何突然的变化或中断。因此,如果函数在该点的值已定义,该点的极限存在,并且函数在该点的值等于极限,则认为函数在该点是连续的。 连续性在机器学习的许多方面都很重要,它能使模型训练平滑,避免损失函数出现不连续的跳跃,从而通过更好的收敛性稳定优化。许多典型的激活函数,如 Sigmoid、ReLU 和 Tanh 都是连续的,因此可以轻松应用基于梯度的学习。此外,连续性确保梯度通过神经网络在反向传播中流动,从而使权重更新稳定。 在机器学习中,平滑的决策制定由连续函数(例如 [此处原文缺失,无法翻译])控制。相反,由早期神经网络中使用的阶跃函数等引起的不连续性,会导致输出的突然变化,从而导致不稳定性。确保模型中使用的函数是连续的,可以提高性能、可靠性,因此是机器学习中的一个基本概念。 代码 输出  现在我们将借助极限和连续性来演示梯度下降的工作原理。 应该指出,理解导数的定义是必需的,而梯度下降方法正是基于此运作的。导数显示了变化率;这在参数值中有所不同,有助于引导模型朝着成本函数上的最小点碰撞。如果极限定义不当,其梯度可能会变得未定义,并可能使优化变得有问题。 连续函数没有突然的变化或跳跃。梯度下降需要一个连续且可微分的成本函数,以实现尽可能平滑的学习。成本函数的突然变化将导致参数的突然变化,从而导致学习建立中的不稳定。  代码 输出 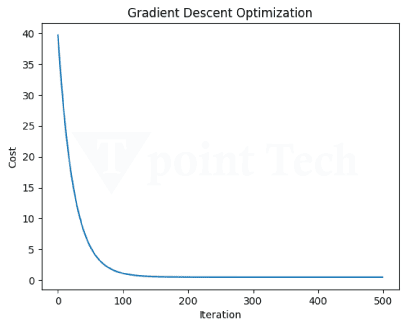 |
关联规则学习是一种无监督学习技术,它检查一个数据项对另一个数据项的依赖性,并进行相应映射以使其更有利可图。它试图在变量之间找到一些有趣的关系或关联...
阅读 3 分钟
在机器学习中,数据增强是一种常用方法,通过处理现有数据来人为地增加训练数据集的大小。为了提高机器学习模型的效率和灵活性,数据增强旨在增加数据的多样性和波动性...
阅读 6 分钟
信用卡欺诈是指某人未经持卡人知情而使用他人信用卡进行金融交易。信用卡是为了帮助消费者提高购买力而创建的,它们是与银行的协议,允许用户花费银行借出的钱...
阅读 6 分钟
元学习通常被称为“学习如何学习”,是计算机科学中一类机器学习。它通过根据实验结果修改学习算法的特定组件来用于提高学习算法的结果和性能。元学习使研究人员能够...
阅读 6 分钟
机器学习有各种基本的数学结构,其中雅可比矩阵和梯度被认为是用于训练神经网络、对输入敏感的模型以及优化的最突出的结构之一。梯度是标量函数的偏导数组成的向量...
阅读9分钟
数据是任何技术最重要的因素之一。同样,数据在机器学习和人工智能中开发智能机器和系统的开发中起着至关重要的作用。在机器学习中,当我们训练模型时,模型的目标是表现良好并获得高……
7 分钟阅读
在训练期间,torch.nn.Dropout() 以给定概率将输入的某些部分设置为零。当通过正则化启用此技术时,可以防止过拟合。但是,需要注意的是,此方法仅适用于非复数值输入。语法它具有...
5 分钟阅读
什么是自动化机器学习?自动化机器学习,或称AutoML,是一个管理机器学习并使其自动化以解决实际问题的分支。它有助于使机器学习任务对机器学习专家、研究人员以及数据科学经验较少的人员来说更简单、更容易访问...
阅读 8 分钟
半监督学习简介:半监督学习是一种机器学习算法,它介于监督学习和无监督学习算法之间。它在训练期间结合使用有标签和无标签的数据集。在理解半监督学习之前,你应该了解机器学习的主要类别......
阅读 4 分钟
简介稳健回归是一种特殊的回归分析形式,它在数据不理想的情况下可以产生强大的校正实现。确切地说,它旨在在存在异常值、缺失值或噪声的情况下产生可靠且准确的结果....
7 分钟阅读
我们请求您订阅我们的新闻通讯以获取最新更新。

我们提供所有技术(如 Java 教程、Android、Java 框架)的教程和面试问题
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
